Boolean Theorems
The basic Boolean theorems that are useful in manipulating and simplifying Boolean expressions are discussed. For convenience, we divide the theorems into two groups:
- (i) Single variable theorems
- (ii) Multivariable theorems
Single variable theorems.
These theorems refer to the condition when only one input to the logic gate is variable.
Table 1 gives single variable Boolean theorems.
| Theorem 1 : | \(A + 0 = A\) |
| Theorem 2 : | \( A · 1 = A\) |
| Theorem 3 : | \(A + \overline{A} = 1\) |
| Theorem 4 : | \(A · \overline{A} = 0\) |
| Theorem 5 : | \(A + A = A\) |
| Theorem 6 : | \(A · A = A\) |
| Theorem 7 : | \(A + 1 = 1\) |
| Theorem 8 : | \(A · 0 = 0\) |
| Theorem 9 : | \(A = \overline{\overline{A}}\) |
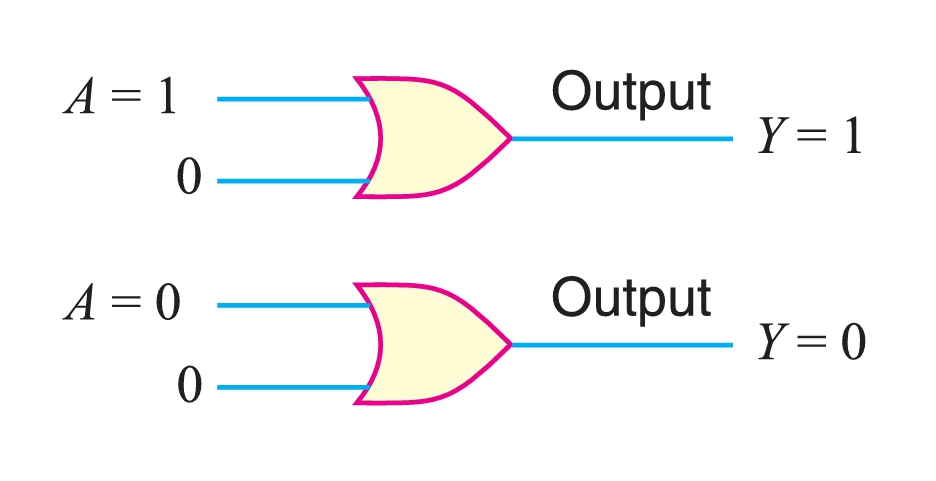
- Theorem 1. \((A + 0 = A)\).
This theorem can be verified by ORing a variable \(A\) with a 0 and is illustrated in Fig. 1. Here, one input to the OR gate is always 0, and the other input \(A\) can be a value 1 or 0. When \(A\) is at 1, the output is 1, which is equal to \(A\). When \(A\) is at 0, the output is 0, which is also equal to \(A\) (= 0). Therefore, a variable ORed with 0 is equal to the value of the variable. This is easy to remember since 0 added to anything does not affect the value of the variable, either in regular addition or OR addition.
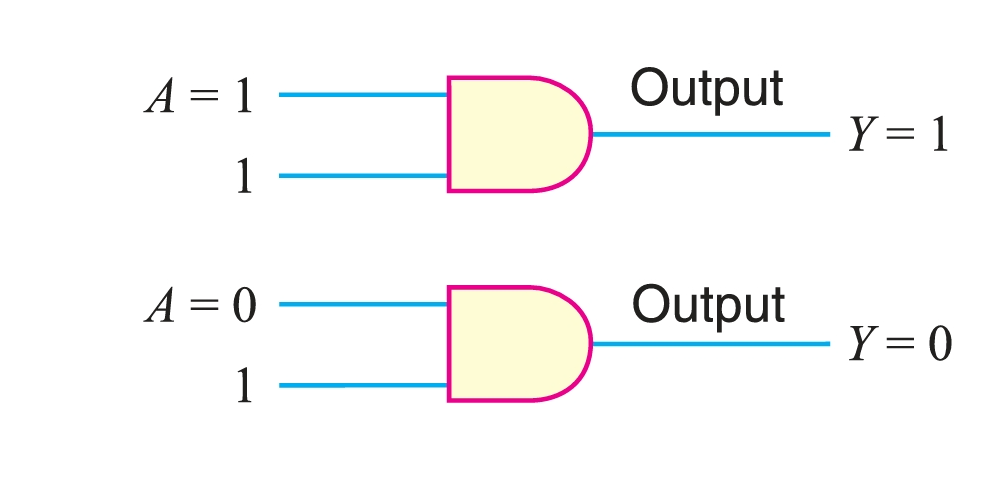
- Theorem 2. \((A . 1 = A)\).
This theorem can be verified by ANDing a variable \(A\) with a 1 and is illustrated in Fig. 2. Here, one input to the AND gate is always 1, and the other can be a value of 1 or 0. If \(A\) is 1, the output of the AND gate is 1 because both the inputs are now 1’s. If \(A\) is 0, the output of the AND gate is a 0. Therefore, a variable ANDed with a 1 is equal to the value of the variable \((A · 1 = A)\). This is easy to remember because the AND operation is just like ordinary multiplication.
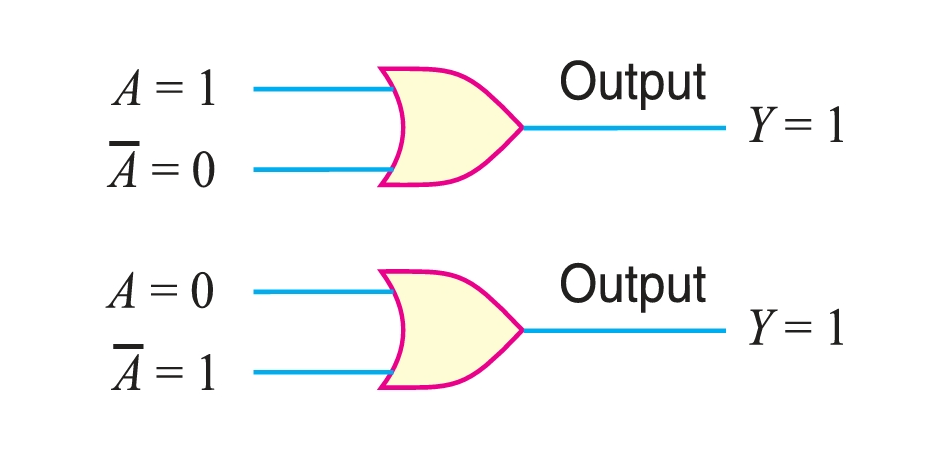
- Theorem 3. \((A + \overline{A} = 1 ). \)
This theorem can be easily explained. If a variable \(A\) and its complement (\overline{A}) are ORed, the result is always 1. If \(A\) is a 0, then \(0 +\overline{0} =0 +1 =1\). If \(A\) is a 1, then \(1+ 1= 1 +0 =1\).
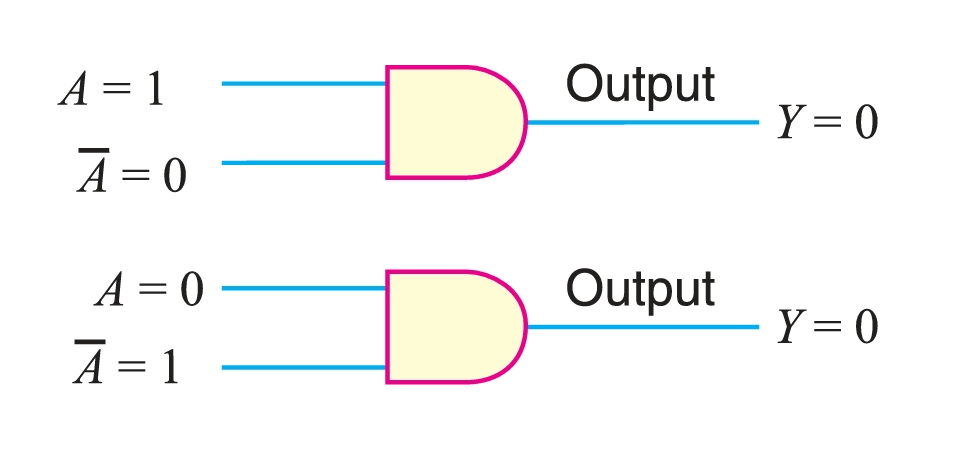
- Theorem 4. \((A · \overline{A}=0 ).\)
This theorem states that if a variable \(A\) is ANDed with its complement, the result is zero. This is readily apparent because either \(A\) or \(\overline{A}\) will always be 0. Therefore, when one of the inputs to an AND gate is 0, the output is always 0.
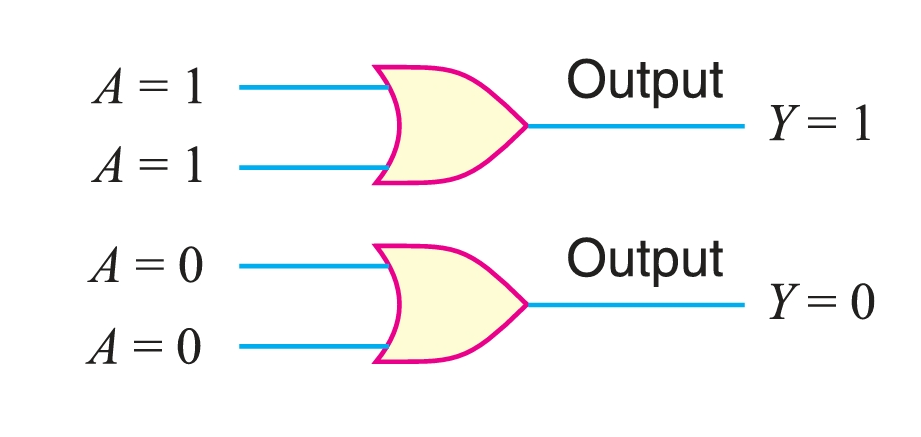
- Theorem 5. \((A+ A= A ).\)
This theorem states that when a variable \(A\) is ORed with itself, the output is equal to the variable. Thus, if \(A\) is a 0, then \(0 + 0 = 0\) and if \(A\) is a 1, then \(1 + 1 = 1\).
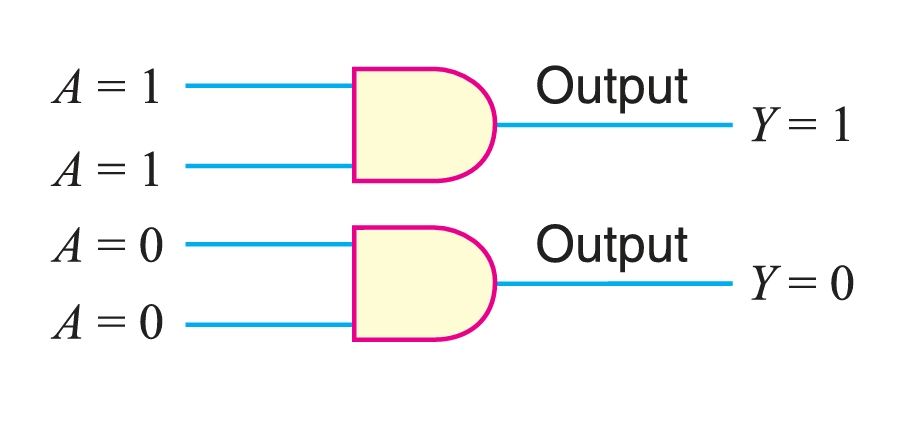
- Theorem 6. \((A · A = A)\).
This theorem states that if a variable \(A\) is ANDed with itself, the result is equal to the variable. For example, if \(A = 0\), then \(0·0 = 0\) and if \(A = 1\), then \(1 · 1 = 1\). For either case, the output of an AND gate is equal to the value of the input variable \(A\).
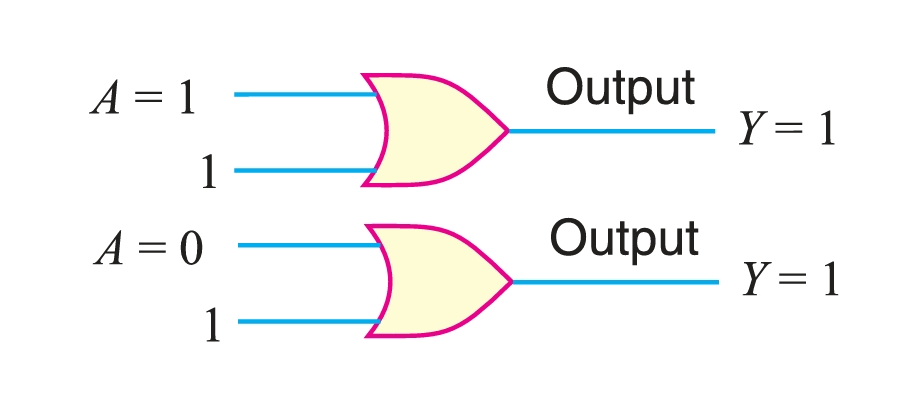
- Theorem 7. \((A + 1 = 1)\).
This theorem states that when a variable \(A\) is ORed with 1, the output is always equal to 1. One input to an OR gate is always 1, and the other input \(A\) can be either 1 or 0. Now, 1 on an input to an OR gate produces 1 on the output regardless of the value of the variable on the other input.
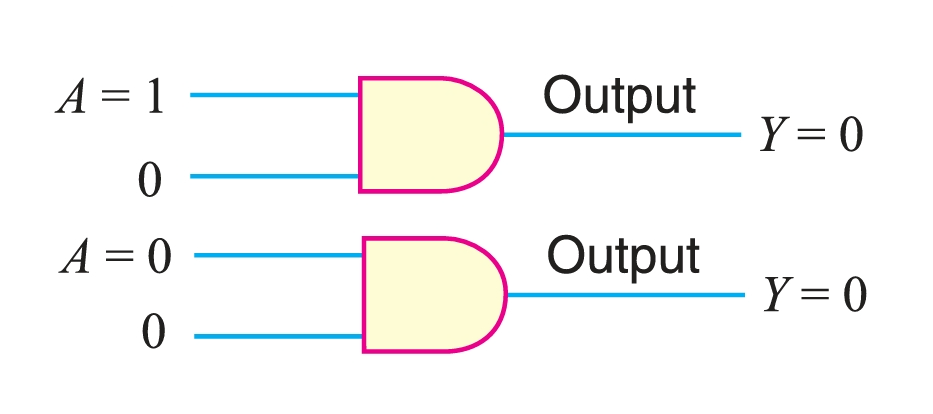
- Theorem 8. \((A · 0 = 0)\).
This theorem states that variable \(A\) ANDed with 0 always produces 0. Recall that any time one input to an AND gate is 0, the output is 0 regardless of the value of the variable \(A\) on the other input.
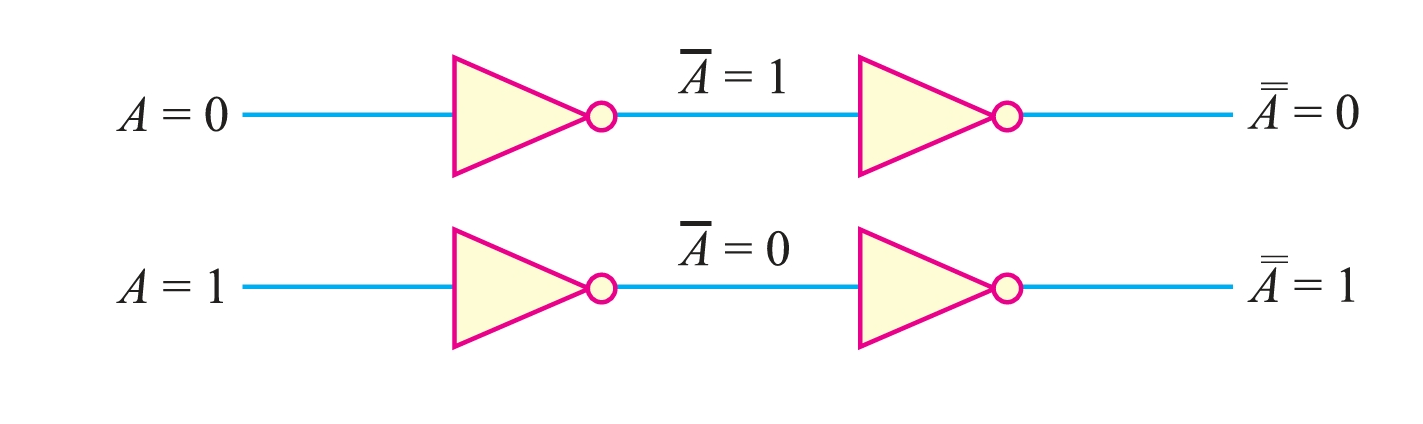
- Theorem 9. \((\overline{\overline{A}} = A ).\)
This theorem states that if a variable \(A\) is complemented twice, the result is the variable itself. Starting with \(A\) and inverting (complementing) it once yields \(A\). Inverting it once more yields \(A\) — the original value.
- Duality Principle. Before moving to multivariable theorems, this would be the right place to mention an important property of Boolean algebra called the duality principle. It is stated below:
The duality principle states that a Boolean expression remains valid if operators OR and AND are interchanged and 1’s and 0’s in the expression are also interchanged.
In order to understand this principle, consider the Boolean Theorem 1, viz.
\[A + 0 = A\]
According to the duality principle, this Boolean expression remains valid if the OR function is replaced by the AND function and 0 by 1. In that case, the Boolean expression becomes:
\[A · 1 = A\]
This is Boolean Theorem No. 2. Therefore, Boolean Theorem 2 is dual of Boolean Theorem 1 and vice versa. Applying the duality principle, Theorem 4 is dual of Theorem 3 and vice versa, Theorem 6 is dual of Theorem 5 and vice versa, Theorem 8 is dual of Theorem 7 and vice versa. To apply the duality principle to a Boolean expression, we simply interchange the OR and AND operators and replace 1’s by 0’s and 0’s by 1’s.
Multivariable theorems
These theorems refer to the condition when more than one input to the logic gates is variable.
Table 2 gives multivariable Boolean theorems.
| Theorem 10 : | \(A + B = B + A\) | Commutative Law |
| Theorem 11 : | \( A · B = B · A\) | |
| Theorem 12 : | \(A + (B + C) = (A + B) + C\) | Associative Law |
| Theorem 13 : | \(A · (B · C) = (A · B) · C\) | |
| Theorem 14 : | \(A · (B + C) = A · B + A · C\) | Distributive Law |
| Theorem 15 : | \((A + B) · (C + D) = A · C + B · C + A · D + B · D\) | Distributive Law |
| Theorem 16 : | \(A + A · B = A\) | Distributive Law |
| Theorem 17 : | \(\overline{(A +B)}=\overline{A} · \overline{B}\) | De Morgan's Theorems |
| Theorem 18 : | \(\overline{(AB)}= \overline{A} + \overline{B}\) | De Morgan's Theorems |
The following points may be noted about these theorems:
(a) Theorems 10 and 11 obey the commutative law. This law states that the order in which the variables are ORed or ANDed makes no difference.
(b) Theorems 12 and 13 obey the associative law. This law states that when ORing or ANDing several variables, the result remains the same regardless of the order in which the variables are grouped.
(c) Theorems 14 and 15 obey the distributive law. This law states that a Boolean expression can be expanded by multiplying term-by-term just the same as in ordinary algebra.
(d) We will prove Theorem 16 by factoring and using Theorems 2, 7, 10, and 14.
\(A + AB \) = \( A\) \(A + A · B \) = \(A · 1 + A · B \) Theorem 2 = \(A · (1 + B)\) Theorem 14 = \(A · (B + 1)\) Theorem 10 = \(A · 1\) Theorem 7 = \(A\) Theorem 2 (e) Theorems 17 and 18 are the two most important theorems of Boolean algebra and were contributed by the great mathematician De Morgan. Therefore, these theorems are called De Morgan’s theorems.