Minterms and Maxterms
In Boolean algebra and digital logic design, the concepts of minterms and maxterms are fundamental because they provide a systematic way to represent and analyze logical functions.
- A minterm is defined as a product (AND) term in which each variable of the function appears exactly once, either in its complemented form or in its uncomplemented form.
- A maxterm, on the other hand, is a sum (OR) term in which each variable of the function also appears exactly once, either complemented or uncomplemented.
These two constructs are closely tied to the truth table of a Boolean function, with minterms corresponding to the rows where the output is 1 and maxterms corresponding to the rows where the output is 0. Together, minterms and maxterms form the basis of canonical representations of Boolean functions, namely the Sum-of-Products (SOP) form and the Product-of-Sums (POS) form.
Minterms are product terms that evaluate to 1 for exactly one row of the truth table, and they form the basis of the canonical SOP form. Maxterms are sum terms that evaluate to 0 for exactly one row of the truth table, and they form the basis of the canonical POS form. Both minterms and maxterms ensure that every Boolean function can be represented completely and unambiguously, serving as the foundation for simplification techniques and practical circuit design.
Maxterms are the dual of minterms.
To understand minterms more clearly, consider a Boolean function with two variables, \(A\) and \(B\). The possible input combinations are \(00\), \(01\), \(10\), and \(11\). For each of these combinations, we can write a minterm.
- For \(A = 0\) and \(B = 0\), the minterm is \(\overline{A}\overline{B}\), because \(A\) is \(0\), so it appears complemented, and \(B\) is \(0\), so it also appears complemented.
- For \(A = 0\) and \(B = 1\), the minterm is \(\overline{A}B\), because \(A\) is \(0\), so it appears complemented, and \(B\) is \(1\), so it appears uncomplemented.
- For \(A = 1\) and \(B = 0\), the minterm is \(A\overline{B}\), and
- For \(A = 1\) and \(B = 1\), the minterm is \(AB\).
- Each minterm evaluates to \(1\) for exactly one row of the truth table and \(0\) for all others.
- If a Boolean function outputs \(1\) for certain rows, then the canonical SOP form of the function is the OR of the minterms corresponding to those rows.
For example, if the function outputs 1 when \(A = 0\), \(B = 1\) and when \(A = 1\), \(B = 0\), then the canonical SOP expression is \(\overline{A}B + A\overline{B}\). This systematic procedure ensures that the function is represented completely and unambiguously.
The above two variable minterms can alternatively be represented by \(m_{0}\), \(m_{1}\), \(m_{2}\), and \(m_{3}\), respectively. For an n-variable problem, there can be \(2^{n}\) number of minterms.
| \(A\) | \(B\) | \(Y\) |
|---|---|---|
| 0 | 0 | \(m_{0}\) |
| 0 | 1 | \(m_{1}\) |
| 1 | 0 | \(m_{2}\) |
| 1 | 1 | \(m_{3}\) |
The truth table can also be expressed in the form of minterms as given below:
\[F (A,B) = \sum (m_{0}, m_{1}, m_{2}, m_{3})\]
For example, A truth table of the XOR gate is given below:
| \(A\) | \(B\) | \(Y\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The Boolean expression of the XOR gate in the form of Minterms is:
\[F(A,B) = \sum (1, 2)\]
Note that the equation only consider the equivalent decimal values for the output 1. All the Zeros omitted.
For the same two-variable example, the maxterms are written as OR terms.
- For \(A = 0\) and \(B = 0\), the maxterm is \(A + B\), because \(A\) is \(0\) so it appears uncomplemented, and \(B\) is \(0\) so it also appears uncomplemented.
- For \(A = 0\) and \(B = 1\), the maxterm is \(A + \overline{B}\), because \(A\) is \(0\), so it appears uncomplemented, and \(B is 1\), so it appears complemented.
- For \(A = 1\) and \(B = 0\), the maxterm is \(\overline{A} + B\), and
- For \(A = 1\) and \(B = 1\), the maxterm is \(\overline{A} + \overline{B}\).
- Each maxterm evaluates to 0 for exactly one row of the truth table and 1 for all others.
- If a Boolean function outputs 0 for certain rows, then the canonical POS form of the function is the AND of the maxterms corresponding to those rows.
For example, if the function outputs \(0\) when \(A = 0\), \(B = 0\), and when \(A = 1\), \(B = 1\), then the canonical POS expression is \((A + B)(\overline{A} + \overline{B})\).
The above two variable Maxterms can alternatively be represented by \(M_{0}\), \(M_{1}\), \(M_{2}\), and \(M_{3}\), respectively. For an n-variable problem, there can be \(2^{n}\) number of Maxterms as well.
| \(A\) | \(B\) | \(Y\) |
|---|---|---|
| 0 | 0 | \(M_{0}\) |
| 0 | 1 | \(M_{1}\) |
| 1 | 0 | \(M_{2}\) |
| 1 | 1 | \(M_{3}\) |
The truth table can also be expressed in the form of minterms as given below:
\[F (A,B) = \prod (M_{0}, M_{1}, M_{2}, M_{3})\]
Now, the Boolean expression of the XOR gate in the form of Maxterms is:
\[F(A,B) = \prod (0, 3)\]
Note that the equation only consider the equivalent decimal values for the output 0. All the 1s omitted.
This duality between minterms and maxterms highlights the symmetry in Boolean algebra, showing how both can be used to represent the same function in different canonical forms. By expressing a function in terms of minterms, the logic circuit of the function can be directly implemented using AND gates for the product terms and OR gates to combine them. Similarly, by expressing a function in terms of maxterms, the logic circuit of the function can directly be implemented using OR gates for the sum terms and AND gates to combine them. This direct mapping from truth tables to hardware makes minterms and maxterms essential tools in the design of combinational circuits such as multiplexers, decoders, and arithmetic units.
Canonical Form of Boolean Expression
The canonical form of a Boolean expression is a standardized way of representing logical functions using either minterms or maxterms, ensuring that every possible variable appears in each term of the expression. This form is extremely important in digital logic design and Boolean algebra because it provides a systematic and unambiguous representation of any Boolean function directly from its truth table.
There are two types of canonical forms:
- The Sum-of-Products (SOP) form and
- The Product-of-Sums (POS) form.
In the canonical SOP form, the Boolean function is expressed as the logical OR of minterms, where each minterm corresponds to a row in the truth table where the output is 1. A minterm is an AND term that includes all variables in either complemented or uncomplemented form, depending on the input values of that row.
For example, if a truth table has output 1 when \(A = 1\) and \(B = 0\), the corresponding minterm is \(A\overline{B}\). By combining all such minterms, the canonical SOP expression is obtained.
On the other hand, in the canonical POS form, the Boolean function is expressed as the logical AND of maxterms, where each maxterm corresponds to a row in the truth table where the output is 0. A maxterm is an OR term that includes all variables in either complemented or uncomplemented form, depending on the input values of that row. For instance, if a truth table has output \(0\) when \(A = 1\) and \(B = 0\), the corresponding maxterm is \((\overline{A} + B)\). By combining all such maxterms, the canonical POS expression is obtained.
The examples of canonical equations are:
- \(Y = A\overline{B} + \overline{A}B\)
- \(Y = AB\overline{C} + A\overline{B}C + \overline{A}B\overline{C} + ABC \)
- \(Y = AB\overline{C}D + \overline{A}BC\overline{D} + A\overline{B}CD + A\overline{B}C\overline{D} + ABCD\)
- \(Y = (A + \overline{B})(A + B)\)
- \(Y = (A + B + \overline{C})(A + \overline{B} + C)(\overline{A} + B + C)(A + B + C)\)
- \(Y = (\overline{A} + \overline{B} + C + D)(A + B + \overline{C} + D)(A + B + C + D)\)
The canonical form is significant because it guarantees that every Boolean function can be represented in a unique and complete way, regardless of its complexity. This makes it easier to analyze, simplify, and implement functions in digital circuits. Although canonical forms are often not the most efficient for implementation, they serve as a foundation for simplification techniques such as Boolean algebra laws and Karnaugh maps.
By starting with the canonical form, one can systematically reduce the number of terms and variables to obtain a minimal expression that requires fewer logic gates. In digital electronics, canonical forms are implemented using combinations of AND, OR, and NOT gates. In SOP, AND gates are used to form minterms, and their outputs are combined using OR gates. In POS, OR gates are used to form maxterms, and their outputs are combined using AND gates. A crucial aspect of canonical forms is their relationship to truth tables. A truth table provides a complete specification of a Boolean function by listing all possible input combinations and their corresponding outputs. From this truth table, the canonical SOP form can be derived by writing minterms for each row with output 1, while the canonical POS form can be derived by writing maxterms for each row with output 0. This systematic procedure ensures that the canonical form fully represents the function without ambiguity.
Canonical forms also highlight the duality principle in Boolean algebra, which states that every algebraic expression remains valid if the operations and identity elements are interchanged. SOP and POS are duals of each other, and this duality emphasizes the symmetry in Boolean logic.
Sum-of-Products Form
The sum-of-products form of a Boolean expression consists of two or more AND terms (i.e., products) that are ORed together. For example, \(Y = AB + CD\) is a sum-of-products expression. Here, AND terms \(AB\) and a are ORed (added). Other examples of this form are :
- (i) \(Y = ABC + \overline{A}B\overline{C}\)
- (ii) \(Y = A\overline{B}C + DEF + A\overline{E}F\)
- (iii) \(Y= \overline{A} + B\overline{C}D + EF\overline{G}\)
The sum-of-products is a very useful form of a Boolean expression due to the straightforward manner in which it can be implemented in logic gates. It has simply two steps: ANDing and then ORing. Therefore, this form is always only a two-level gate network, i.e., the maximum number of gates through which a signal must pass in going from input to output is two, excluding the NOT gate.
Product-of-Sums Form
The Product-of-Sum (POS) form of a Boolean expression is one of the two standard canonical forms used in digital logic design; the other is the Sum-of-Products (SOP) form. In POS, a Boolean function is expressed as the logical AND (product) of several logical OR (sum) terms. The product-of-sums form of a Boolean expression consists of two or more OR terms (i.e., sums) that are ANDed together. For example, \(Y = (A + B)(C + D)\) is a product-of-sums expression.
To understand POS, it is essential to recall that Boolean algebra operates with binary variables that can take values of 0 or 1, and its basic operations include AND, OR, and NOT. In the POS form, the OR operation is applied first to variables or their complements, and then the results of these OR terms are combined using the AND operation.
Simplification of Boolean Expressions
The form of a Boolean expression determines how many and which types of logic gates are needed, as well as how they are connected together. The more complicated the Boolean expression, the more complex the logic circuit will be. It is, therefore, desirable to simplify an expression as much as possible to get the simplest logic circuit. Note that the new expression can be used to implement a logic circuit that is equivalent to the original logic circuit but contains fewer gates and connections.
While simplifying a Boolean expression, the following two steps may be very helpful:
- (i) Put the original expression into the sum-of-products form by the repeated use of rules, theorems, and techniques of Boolean algebra.
- (ii) Once it is in this form, the product terms are checked for common factors, and factoring is performed wherever possible.
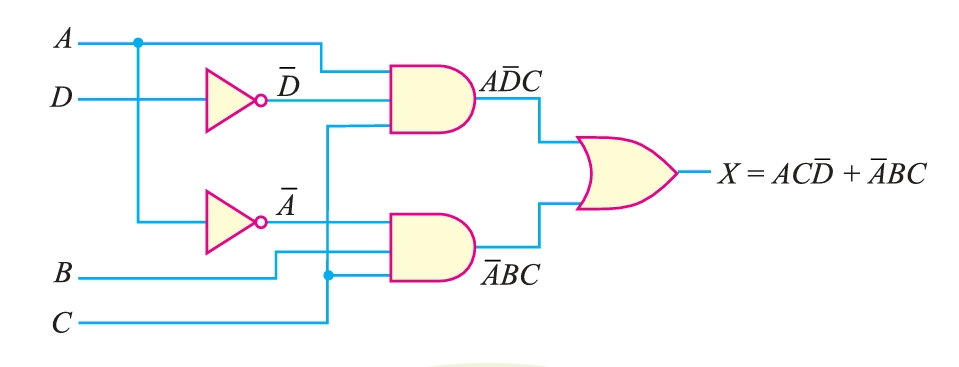
For example, consider the Boolean expression:
\[X = AC\overline{D} + \overline{A}B (CD + BC)\]
We require five AND gates, two OR gates, and two inverters to implement this expression. In all, nine gates are needed. We shall now use laws, rules, and techniques of Boolean algebra to get the simplest expression for the given function.
- Step 1. Apply distributive law to the second term by multiplying the term \(CD + BC\) by \(\overline{A}B\). The result is :
\[X = AC\overline{D} + \overline{ABCD} + \overline{ABBC}\]
- Step 2. Applying the rule BB = B to the third term, we have,
\[X = AC\overline{D} + \overline{A}BCD + \overline{A}BC\]
- Step 3. Note that C is common to every term, so that it can be factored out using distributive law.
\[X = C(A\overline{D} + \overline{A}BD + \overline{A}B)\]
- Step 4. We see that the term \overline{A}B appears in the last two terms within the bracket and can be factored out of those two terms.
\[X = C[A\overline{D} + \overline{A}B(D + 1)]\]
Since \(D + 1 = 1\),
\[X = C(A\overline{D} + \overline{A}B) \]
It appears that this equation cannot be simplified any further, but it can be written in a slightly different way by applying the distributive law (this results in the sum-of-products form):
\[X = AC\overline{D} + \overline{A}BC\]
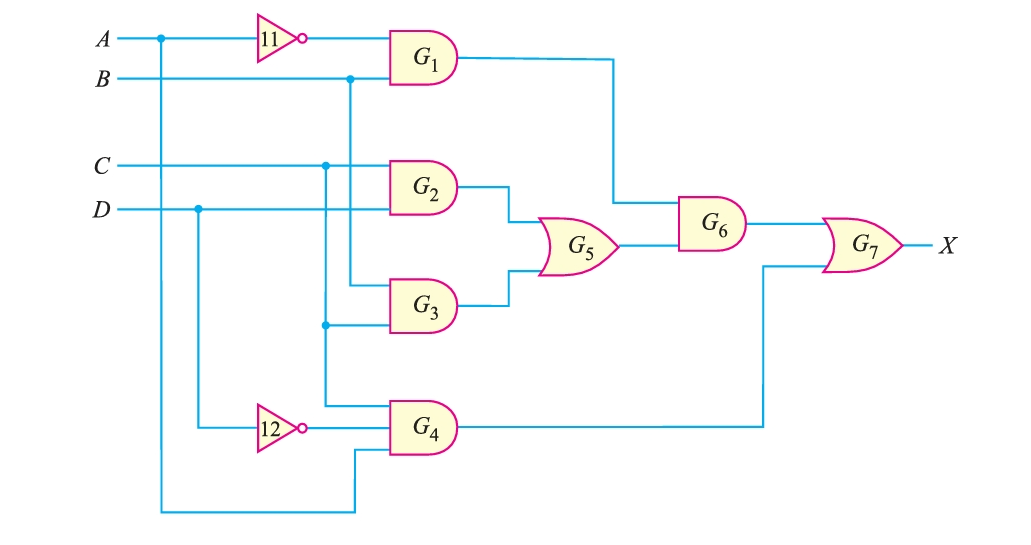
Implementing this equation (i.e., \(X = AC\overline{D} + \overline{A}BC\) ) into the logic circuit, it only requires two three-input AND gates, two inverters, and one two-input OR gate, as shown in Figure 2. This minimized circuit is equivalent to the original circuit in Figure 1, but it requires only five gates (instead of nine).