Karnaugh map (K-map) method:
The Boolean functions can be simplified using the theorems of Boolean algebra. The reduced Boolean expression helps to get the simple, less expensive, and smaller circuit. This method of simplification is not used in practice as it is difficult to apply. Further, it is impossible to guarantee that the reduced expression is minimal, and it cannot be reduced beyond the obtained expression. One is known as the Karnaugh map (K-map) method.
The Karnaugh map method is very commonly used to simplify Boolean expressions since no algebraic rules are applied in this method. It is simply a graphic method and provides a systematic approach for getting the simplified Boolean expression. If this method is properly used, then the available Boolean expression will be minimal and will not further be simplified by any method. The Karnaugh map also called the K-map method, is suitable for simplifying Boolean expression, which contains four or fewer variables (or literals) with their complements. In short, A Karnaugh map is a visual display of the fundamental products needed for a sum-of-products solution.
Two Variable K-map
For two variable K-maps, two lines are drawn: one horizontal and the other vertical. On one line, the complement of one variable followed by the variable itself is written and on the other line, the complement of the other variable followed by that variable itself is written. The two variable K-map can hold 4 values of 4 unique input conditions with 2 variables (\(2^{n} = 4\)), where \(n\) is the number of variables.
Let the two variables be \(A\) and B. So \(A\) and variable \(\overline{A}\) , are written on a vertical line; \(B\) and variable \(\overline{B}\) are written on a horizontal line or otherwise for a corresponding truth table, as shown in figure 2.
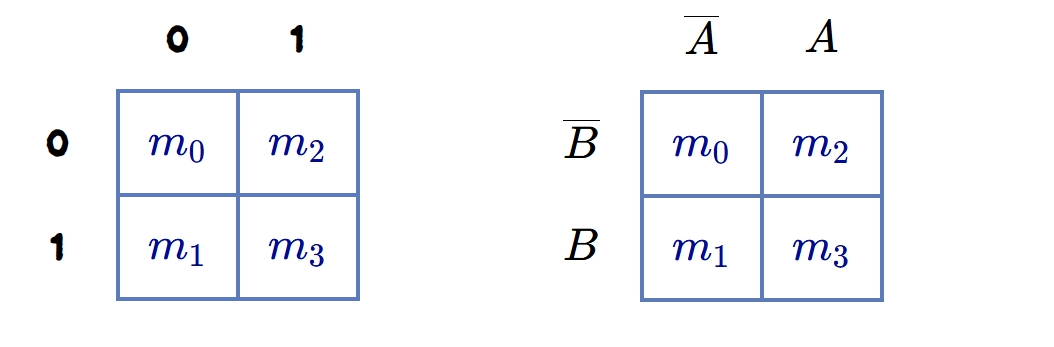
These two figures are similar and show the same meaning. One can use either of the two ways mentioned above. Each K-map show four squares represented by four minterms \(m_{0}\), \(m_{1}\), \(m_{2}\), and \(m_{3}\). In the truth table of two variables if there are 1’s entry corresponding to the some minterms, then 1s are entered corresponding to those minterms.
Let us consider the 2 variable truth table as given below:
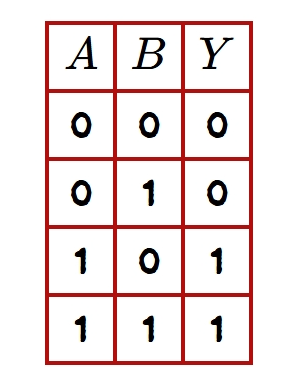
- Its Boolean expression is : \(Y = A\overline{B} + AB\)
- Its Minterm expression is : \(F (A, B) = \sum m(2, 3)\)
- Its Maxterm expression is : \(F (A, B) = \prod M(1, 2)\)
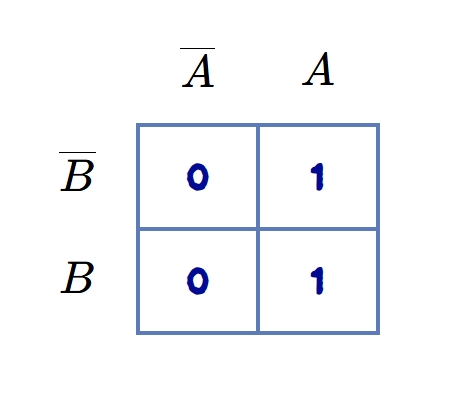
Hence, we have 1s entry for the Minterms, \(m_{2}\) and \(m_{3}\) or we have 0s entry for the Maxterm, \(m_{0}\) and \(m_{1}\). Now,
1 is filled in the Karnaugh cell corresponding to the the fundamental products, \(A\overline{B}\) and \(AB\) or the decimal equivalent of Minterm in the Karnaugh map. The final step in drawing the Karnaugh map is to enter 0s in the remaining spaces (representing the Maxterms). The 2 variable K-map representing the Minterm (or Maxterms) are shown in the figure 3.
Three Variable K-map
For three variables two adjacent variables are taken on either side (vertical line or horizontal line) of the K-map and the remaining one variable on the other side. Only one change in the variable is allowed while shifting from one cell of Karnaugh map to another (either horizontally or vertically). The three variable K-map can hold 8 values for 8 (\(2^{n}\) with \(n\) = 3) unique input conditions, where \(n\) is the number of variables.
Let \(A\), \(B\) and \(C\) are the three variables, the two variables will have four combinations labeled on one side as \(\overline{A}.\overline{B}\), \(\overline{A}.B\), \(A.B\) and \(A.\overline{B}\); \(C\) and \(\overline{C}\) on the other side as shown in figure.
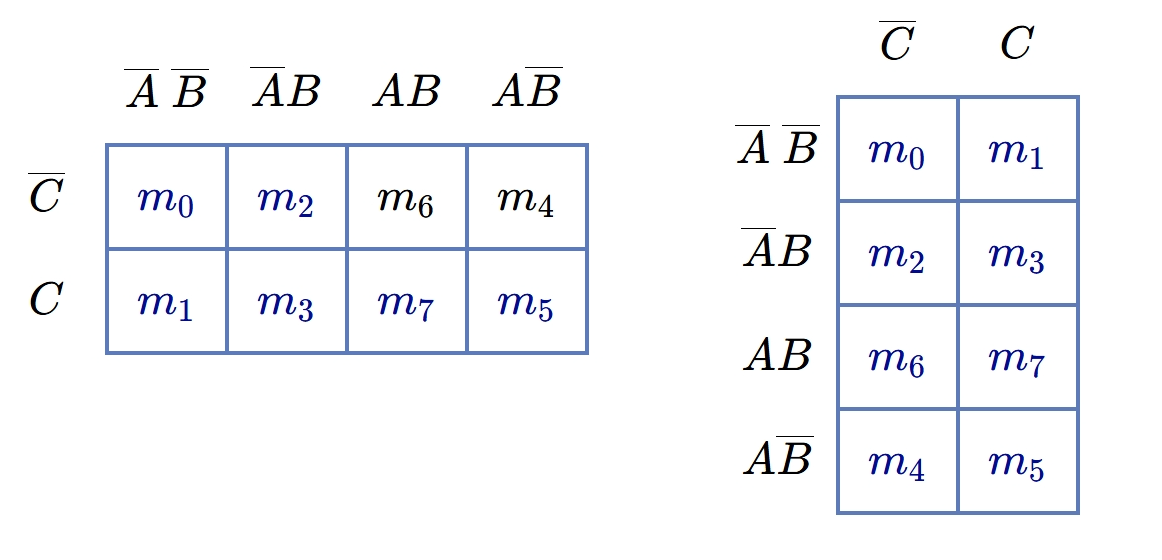
The other method of writing K-map for three variables is that in place of the possible combinations of two variables \(A\) & \(B\) it is written as 00, 01, 11 and 10; and in place of \(\overline{C}\) & \(C\), 0 & 1 are written; as illustrated in figure, where \(AB\) and \(C\) are shown separately over and below of a leaning line.
If a Boolean function of three variables or four variables is given, the \(1\)s entry in the K-map is done for those combinations that are present in the given expression, and for the other combinations, \(0\)s entries are made.
Let us draw the K-maps for the following Boolean function of three variables.
\[F_1(A, B, C) = \sum(m_1, m_3, m_5, m_6, m_7) \]
In the K-map of three variables \(1\)s entries are made for the combinations \(m_1\), \(m_3\), \(m_5\), \(m_6\), \(m_7\), and in the remaining combinations, \(0\)s are entered. The K-map for the same is shown in figure.
- Step 1: Draw the truth table for the function:
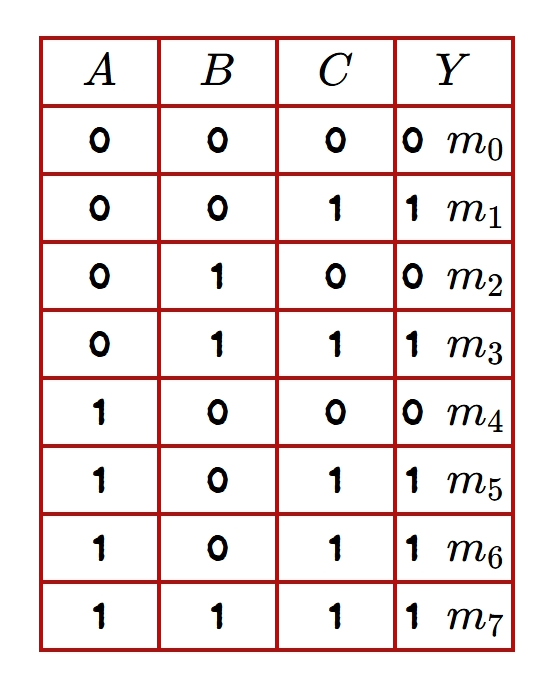
- Step 2: Write down the Boolean expression obtained from the truth table.
\[F_1(A, B, C) = \sum (m_1, m_3, m_5, m_6, m_7) \]
\[F_1(A, B, C) = \sum m(1, 3, 5, 6, 7) \]
\[F_1(A, B, C) = \overline{A}~\overline{B}C + \overline{A}BC + A\overline{B}C+ AB\overline{C} + ABC \]
- Step 3: Fill the
1sin the Karnaugh cells for the Minterms in the Boolean expression.
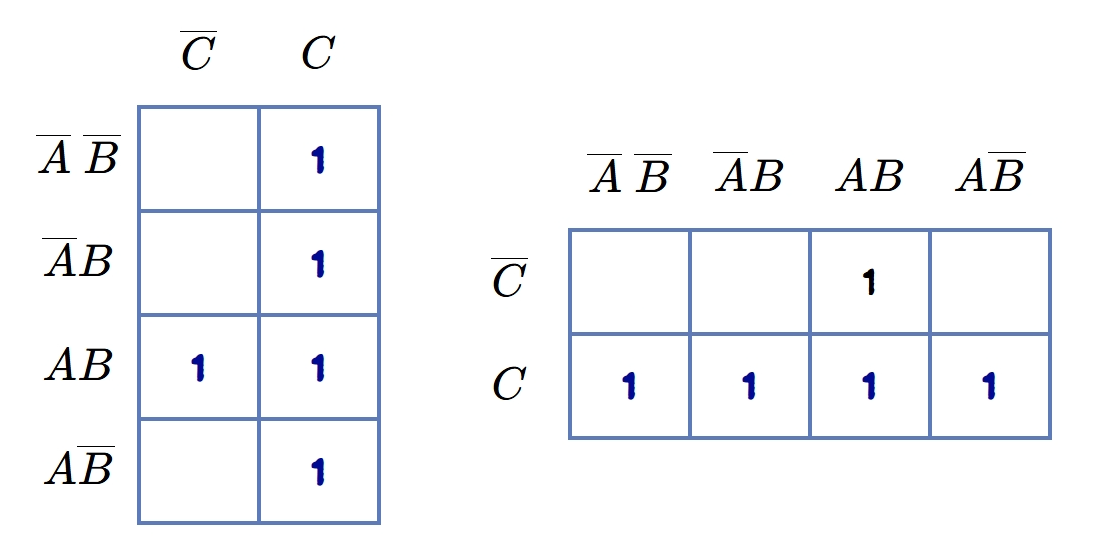
- Step 4: Fill the remaining empty cells with
0s
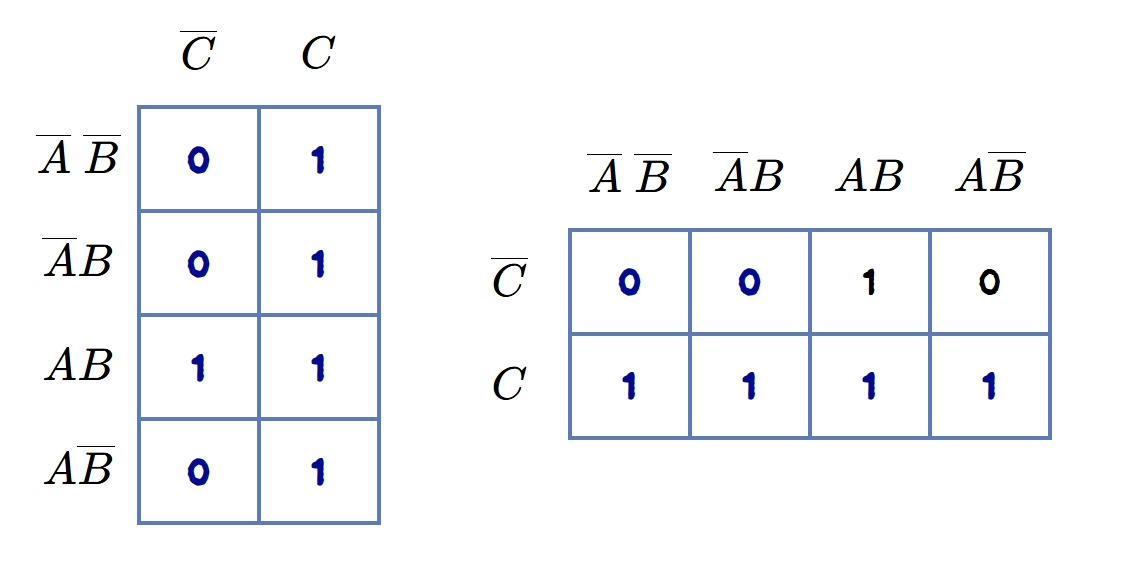
Four Variable K-map
For four variables, two adjacent variables are taken on either side (vertical line or horizontal line) of the K-map, and the two variables are on the other side. Only one change in the variable is allowed while shifting from one cell of Karnaugh map to another (either horizontally or vertically). The four variable K-map can hold 16 output values for 16 (\(2^{n}\) with \(n\) = 4) unique input conditions comparising for 4 unique variables.
Let \(A\), \(B\), \(C\), and \(D\) be the four variables, the two variables will have four combinations labeled on one side as \(\overline{A}\).\(\overline{B}\) , \(\overline{A}\).\(B\) , \(A\).\(B\) and \(A\).\(\overline{B}\); and the other two will also have the four combinations as \(\overline{C}\).\(\overline{D}\) , \(\overline{C}\).\(D\) , \(C\).\(D\) and \(C\).\(\overline{D}\) on the other side as shown in figure.
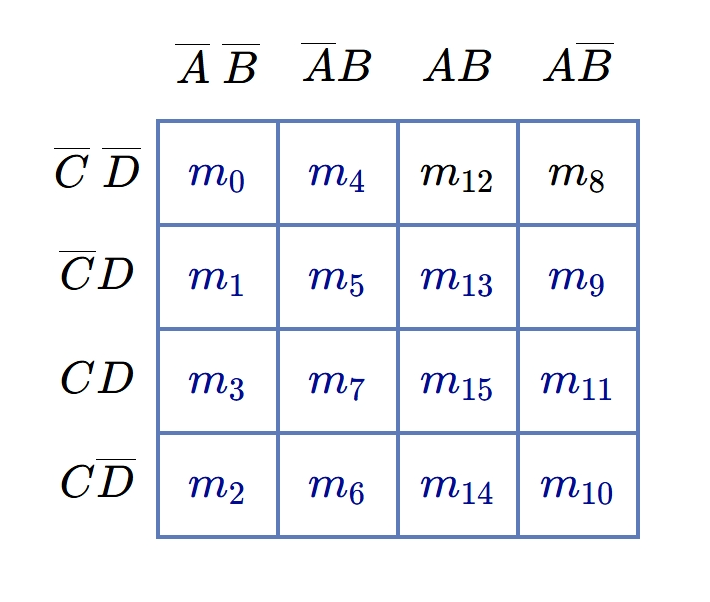
Now, let us draw the K-maps for the following Boolean function of four variables.
\[F (A, B, C) = \sum (m_2, m_3, m_4, m_6, m_7, m_{11}, m_{14}, m_{15})\]
In the K-map of four variables \(1\)s entries are made for the combinations \(m_2\), \(m_3\), \(m_4\), \(m_6\), \(m_7\), \(m_{11}\), \(m_{14}\), \(m_{15}\), and in the remaining combinations, \(0\)s are entered.
- Step 1: Draw the truth table for the function:
- Step 2: Write down the Boolean expression obtained from the truth table. \[F (A, B, C) = \sum (m_2, m_3, m_4, m_6, m_7, m_{11}, m_{14}, m_{15})\] \[F (A, B, C) = \sum m(2, 3, 4, 6, 7, 11, 14, 15)\] \[F (A, B, C) = \overline{A}~\overline{B}C\overline{D} + \overline{A}~\overline{B}CD + \overline{A}B\overline{C}~\overline{D} + \overline{A}BC\overline{D} + \overline{A}BCD + A\overline{B}CD + ABC\overline{D} + ABCD \]
- Step 3: Fill the
1sin the Karnaugh cells for the Minterms in the Boolean expression. - Step 4: Fill the remaining empty cells with
0s
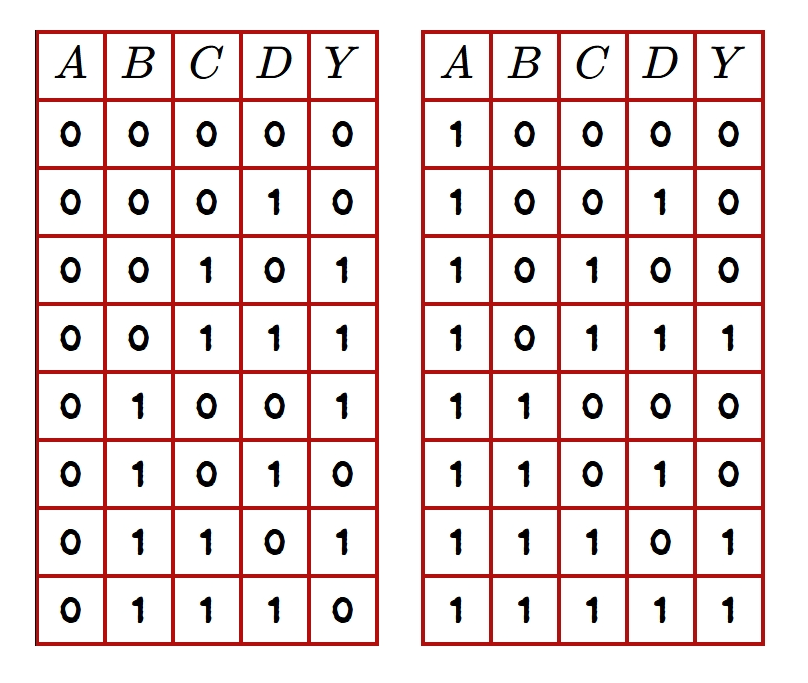
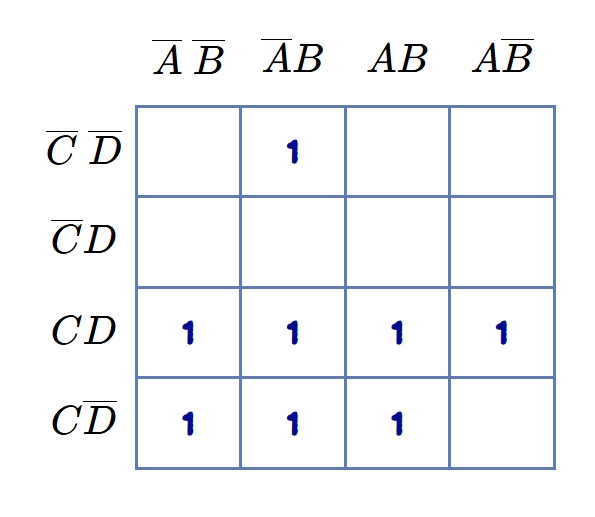
The K-map for the same is shown in figure 9.
Encircling of Groups:
After constructing the K-map, the pairs of quads and octets of adjacent 1s in the K-map are made for getting the minimal Boolean expression. A pair eliminates one variable with its complement; a quad and an octet eliminate two variables and three variables, respectively, with their complements. Now, it will be discussed how pairs, quads, and octets are formed in the K-map and help minimize the Boolean expression.
Pairs:
In the two-variable or four-variable K-map having 1s and 0's entry, two adjacent 1s (vertically or horizontally) are encircled. The diagonally adjacent 1s are never encircled. The encircled 1s form the pairs, as shown in the figure.
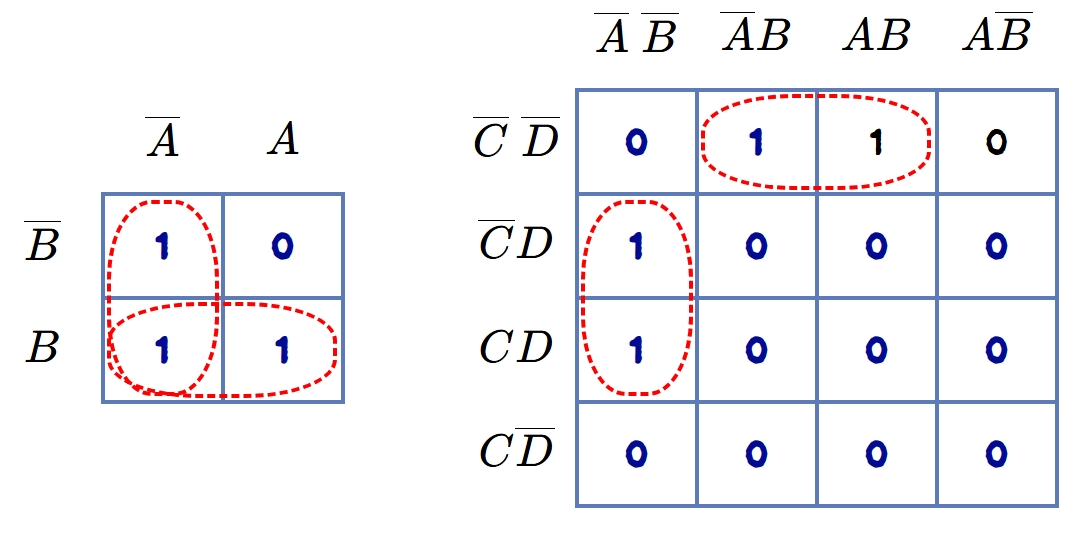
Now it is clear from the K-map of two variables that there are two encircled pairs of adjacent 1s, and these pairs correspond to the terms \(\overline{A}\overline{B}\) and \(\overline{A}B\). The second pair in two variable K-map is \(\overline{A}B\) and \(AB\).
In the four variable case, the two encircled pairs of the adjacent 1s are \(\overline{A}B\overline{C}\overline{D}\) and \(AB\overline{C}\overline{D}\), likewise, \(\overline{A}\overline{B}\overline{C}D\) and \(\overline{A}\overline{B}CD\).
The method of writing these terms is that the variable, which gets changed from complemented form to un-complemented form or vice versa, is dropped with its complement.
This can be illustrated as follows:
Consider the pairs in the two variable K-map, the one variable which is removed from the encircled pair of \(\overline{A}\overline{B}\) and \(\overline{A}B\) is the complemented pair, i.e., B. Hence \(\overline{A}\). In the second encircled case, \(\overline{A}B\) and \(AB\), the minimal variable remains is B as the complemented combination is eleminated.
Similarly, consider the four variable K-map, having the variables, \(\overline{A}B\overline{C}\overline{D}\) and \(AB\overline{C}\overline{D}\), and \(\overline{A}\overline{B}\overline{C}D\) and \(\overline{A}\overline{B}CD\), the final variables left after removing the complemented pairs are, \(B\overline{C}\overline{D}\) and \(\overline{A}\overline{B}D\). The variable \(A\) and \(C\) changes from 1 to 0, so these variables is dropped with its complement. The remaining (common) variables remains (in SOP form).
The Boolean algebra is involved in getting the expression for a pair. In the first encircled pair (discussed above) of two variable K-map, each 1 of the pair shows the terms \(\overline{A}~\overline{B}}\) and \(\overline{A}B}\) (corresponding to binary numbers 00 & 01). When these terms are ANDed, and solved further, \(\overline{A}\) is obtained:
\[ Y = \overline{A}~\overline{B} + \overline{A}B + AB\\ Y = \overline{A}~(\overline{B} + B) + AB\\ Y = \overline{A} + AB\\ Y = (\overline{A} + A) (\overline{A} + B)\\ Y = (\overline{A} + B) \]
Similarly, one can verify the terms corresponding to encircled pairs in four variable K-maps as given in the figure.
From the above discussion, it is clear that a pair eliminates one variable with its complements, i.e., the pair will contain the term of two variables in a three-variable K-map and the term of three variables in a four-variable K-map.
Quads:
In the K-map, if four 1s are adjacent in a row or column or in the form of a square, then these 1s are encircled and called quads. \(A\) term is written for each quad using the same techniques discussed above. The variables that change from complemented to uncomplemented or vice versa are dropped, and the variables that are common in all the four 1s of a quad are considered to write terms in SOP form.
Consider a K-map shown in figure.
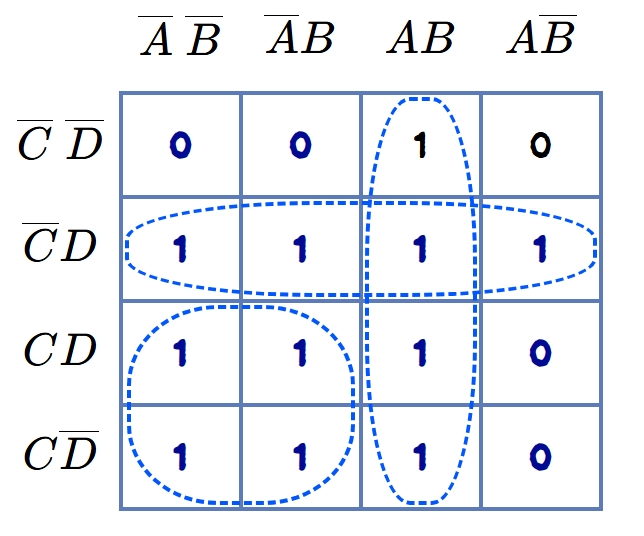
In the K-map of four variables (figure), the encircled group of 1s shows the quad whose four elements represent the binary numbers 0001, 0010, 0011, 0101, 0110, 0111, 1001, 1100, 1101, 1110 & 1111 for variables ABCD. The Boolean algebra is involved in getting the expression for a quad. The quad combines two pairs (shown by dotted encircles in the figure). In the encircled quad, the three pairs will show the terms as
\[ Y = AB + \overline{C}D + \overline{A}C\]
Similarly, the two quads are encircled in the K-map of four variables. One can verify the terms for each quad. It is clearly illustrated that the quad will contain the term of one variable in a K-map of three variables, and it will contain the terms of two variables in the K-map of four variables. It may, therefore, be stated that a quad eliminates two variables with their complements.
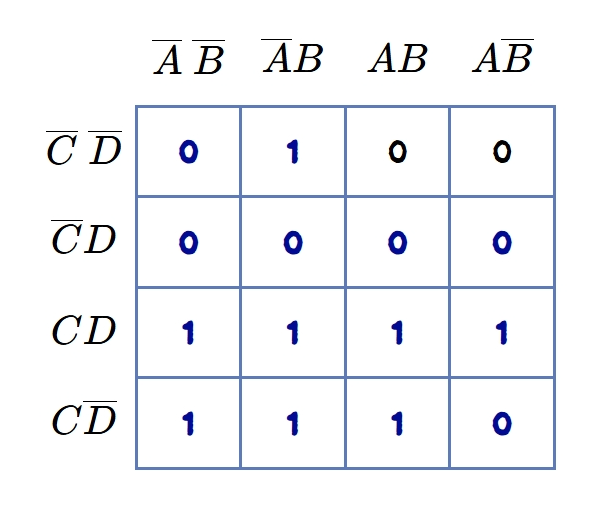
Octets:
The eight adjacent 1s are encircled in a K-map known as an octet. Figure shows the encircled octet in a K-map of 4 variables. The term for the octet is \(B\), written with the same technique used for pairs and quads.
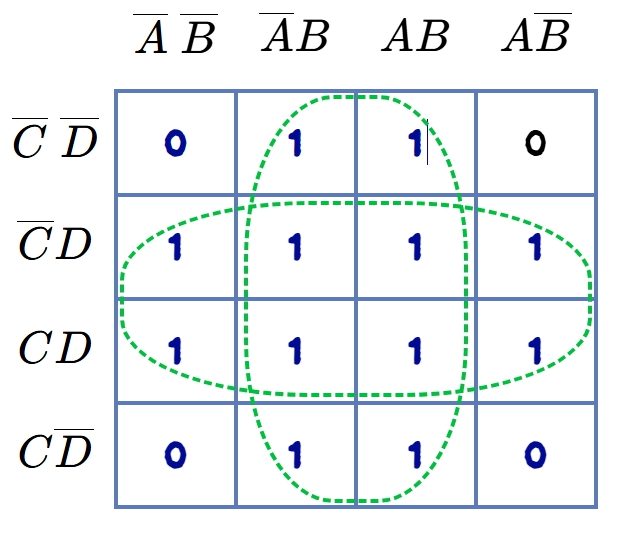
An octet eliminates three variables with their complements and gives a term of one variable in a K-map of four variables. In fact, an octet is a combination of two quads, as as obtained from the figure. The encirlced area shows two octets which eliminates three variables and it gives:
\[ Y = B + D \]
Overlapping groups:
While making encircled groups in the K-map, it is always tried to have the groups of the largest number of 1s first, then others, i.e., octets are encircled first, then quads, and then pairs. It is important to use the same 1 more than once. In other words, same 1 may be used in more than one encircled group. Such groups are called as the overlapped groups. Some overlapped groups are shown in the figure.
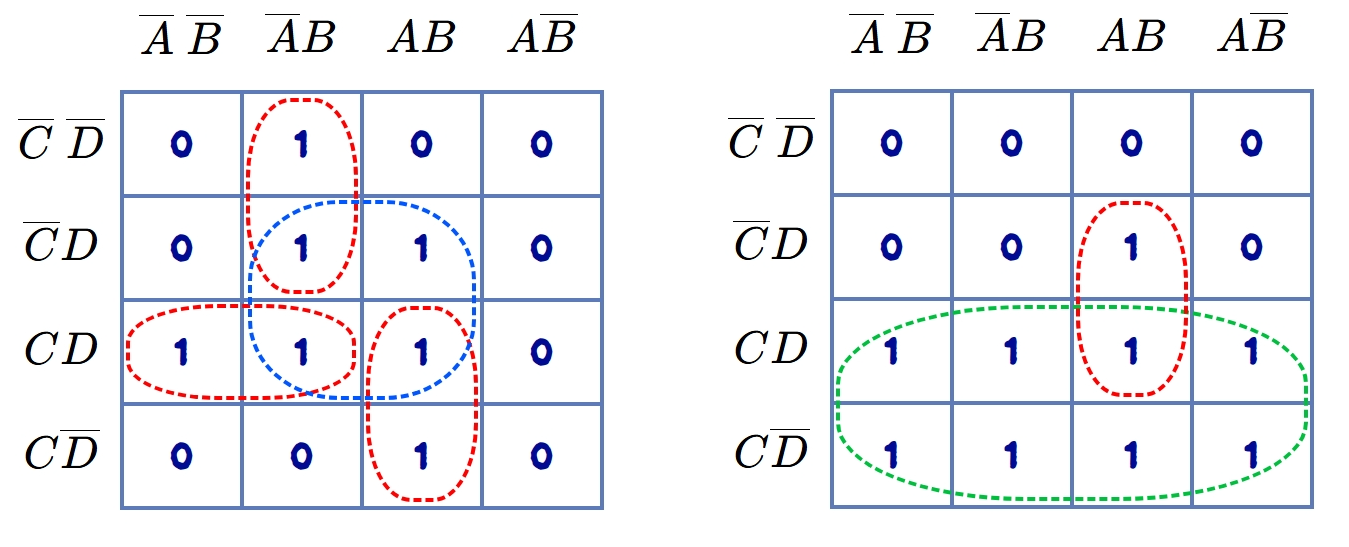
The terms for each encircled group are written in the same manner as is done for regular pairs, quads, and octets.
Rolling groups:
It is also allowed to roll the K-map so that grouping of the largest number of 1s may be formed. To understand this, consider a K-map as shown in figure. In this K-map, while encircling, one can obtain two quads, but using the rolling of the K-map, an octet may be formed as shown in the figure. Here, the rolling is done in such a way that the left-hand side encircled quad touches the right-hand side encircled quad. This looks like an octet. The rolling is shown by half encircling the two groups, as shown in the figure. Thus, the term corresponding to the rolled octet is written in the same fashion as in normal encircling.
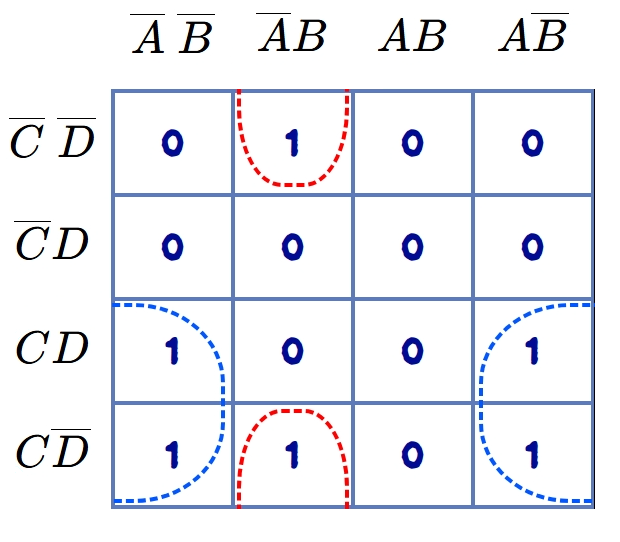
The rolling is possible for quads and pairs as illustrated in the figure.
The rolling is not only possible with the 1s of extreme left columns and the 1s of extreme right columns of the K-map, but it is possible with the 1s of the uppermost row and the 1s of the lowermost column, as shown in the figure.
Redundant Groups:
While encircling the groups in the K-maps, there is a possibility that all the elements (1s) of some groups/groups are overlapped by other groups. Such a group whose all 1s are overlapped by other groups is called a redundant group. The redundant groups may be illustrated by considering a K-map shown in the figure.
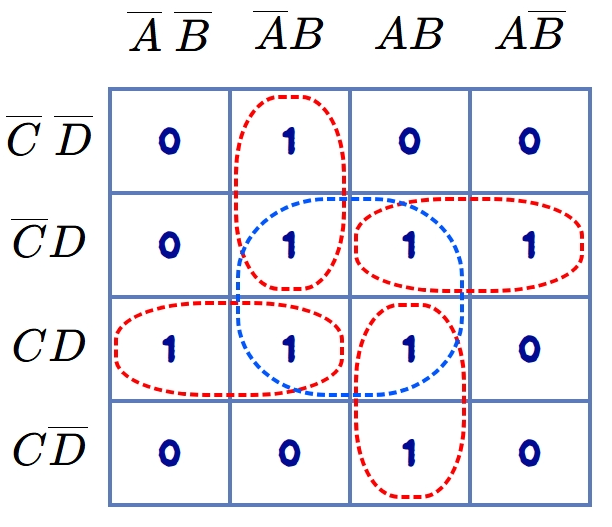
In this K-map, the encircled groups are one quad and four pairs. But quad is redundant since all four 1s are used to form other pairs. The quad is, therefore, eliminated. So, the valid encircled groups will be as shown in the figure.
The encircled groups of this figure are simplified one and the minimal expression of this K-map is given as: \[ F = \overline{A}~ \overline{B}C + B\overline{C}D + \overline{B} C\overline{D} + \overline{A} BC \]
Procedure for Simplification:
The different rules for encircling the groups in the K-map have been discussed in the above sections. Now, using these rules, the method of getting the minimal Boolean expression of the given truth table (or function) will be summarized below:
- After forming the K-map, enter 1s for the min-terms corresponding to 1 in the truth table (or enter 1s for the min-terms of the given function to be simplified). Enter 0s for the remaining min-terms.
- Encircle octets, quads, and pairs, of course, remembering rolling and overlapping. Try to form groups of the maximum number of 1s.
- If any such 1s occur that are not used in any of the encircled groups, then these isolated 1s are encircled separately.
- Review all the encircled groups and remove the redundant groups, if any.
- Write the terms for each encircled group.
- The final minimal Boolean expression corresponding to the K-map will be obtained by ORing all the terms obtained above.
Now, simplify the following Boolean function of three variables using K-map.
\[F(A, B, C) =\sum (m_0, m_1, m_5, m_6, m_7)\]
The K-map for the given function is drawn after encircling the groups of 1s, as shown in figure.
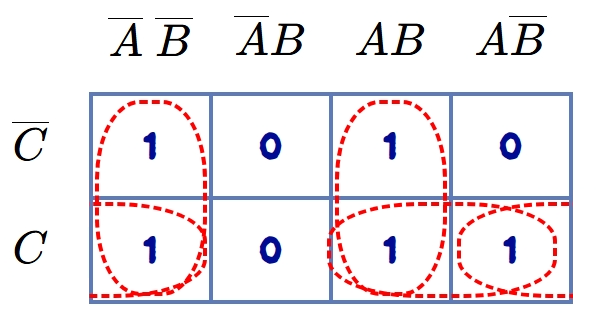
The required Boolean expression is given by:
\[F = \overline{A}~\overline{B}+AB+AC+\overline{B}C\]
Now, simplify the following Boolean function of four variables using K-map. \[F(A,B,C,D,) = \sum m(0,1,3,4,7,8,12,13)\]
The K-map for the given function is drawn, after encircling the groups of 1s, as shown in the figure.
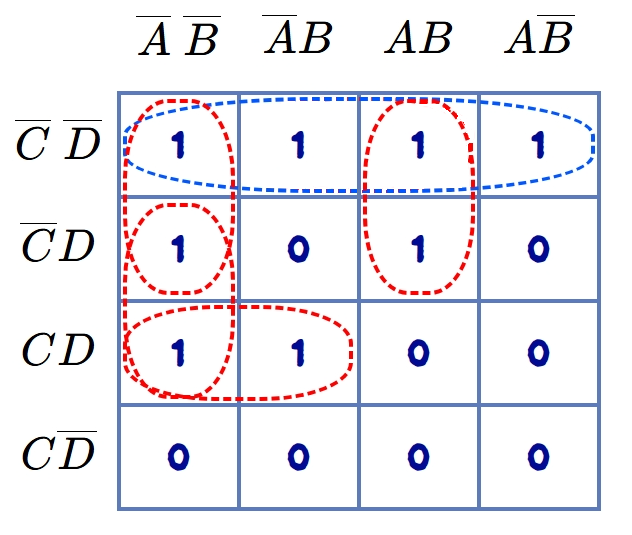
The required Boolean expression is given by:
\[
F = \overline{A}~\overline{B}~\overline{C} + \overline{A}~\overline{B}~\overline{D} + \overline{A}CD +AB~\overline{C} + \overline{C}~\overline{D}
\]
Now, minimize the following function using K-map and realize it with AND, OR & NOT logic gates. \[Y(A,B,C,D,) = \sum m(0,1,5,8,10,11,14,15)\]
The K-map drawn after encircling the groups of 1s, for the given function is shown in figure.
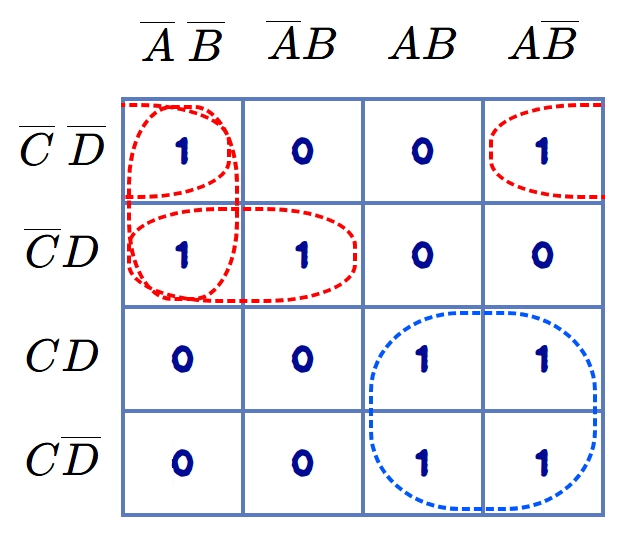
The required Boolean expression is given by:
\[Y = \overline{B}~\overline{C}~\overline{D} + \overline{A}~\overline{B}~\overline{C} + \overline{A}~\overline{C}D + AC\]
It is interesting to note from this figure that the four 1s at the corners of the K-map forms a quad due to the rolling on both sides, whose term will be \(B\) \(D\) .
After getting the minimal Boolean expression, the realization of the function will be as shown in the figure.
Incompletely Specified Functions and Don't Care Condition:
In digital circuits, we come across two types of functions, namely completely specified functions and incompletely specified functions. The functions whose values are specified for all min-terms are known as completely specified functions, and in the K-map, either 0s or 1s are entered for all the min-terms; such functions have been considered so far. But sometimes, we encounter situations in which some min-terms do not occur.
In the K-map, φ is entered for every incompletely specified function. The φ is called the don't care condition. While encircling the groups in the K-map φ may be assumed to be either 0 or 1, whichever helps give the simplest expression. The don't care are treated as 1s inside encircled groups in the K-map and are treated as 0s outside the encircled groups. This can be illustrated by taking an example. Suppose we wish to minimize the following function of four variables having the 'don't care' also. The 'don't care' is shown by φ below the summation symbol.
\[X (A, B, C) = \sum (2,7)+\sum_{\phi} (3,6)\]
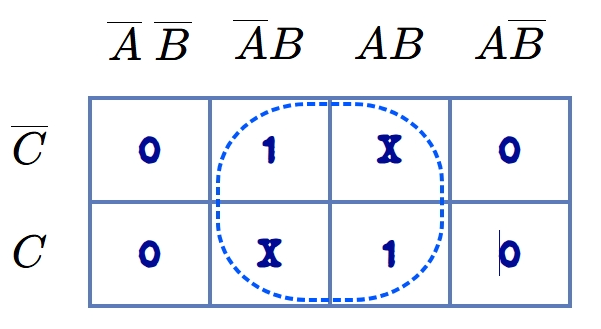
This function shows that in the K-map, 1s are entered corresponding to the minterms 2, 7, and φ are entered for 3, 6, and 0s are entered for the remaining terms. The K-map with these entries is shown in the figure, and its encircling & simplification are shown in the figure. There are two encircled quads, and φ, which are inside the encircled groups, are treated as 1s. The last column of this K-map is not encircled to form the quad, as all its elements are φ. It must be remembered that no such group is formed whose all the elements are φ. The minimal Boolean function of this K-map is given by:
\[Y = B\]
The general procedure of getting the minimal Boolean expression of a K-map, including the 'don't care' conditions, is summarized below
- After forming the K-map, enter 1s for the min-terms corresponding to 1 in the truth table (or enter 1s for the min-terms of the given function to be simplified). Enter φ to the ‘don't care' conditions and 0s for the remaining min-terms.
- Remembering rolling and overlapping, encircle octets, quads, and pairs. The φ may be treated as 1 if these help in forming the largest groups. No such group will be formed whose all the elements are φ.
- If any such 1s occur that are not used in any of the encircled groups, then these isolated 1s are encircled separately.
- Review all the encircled groups and remove the redundant groups, if any.
- Write the terms for each encircled group.
- The final minimal Boolean expression corresponding to the K-map will be obtained by ORing all the terms obtained above.
Now, minimize the following function using K-map and realize it with NAND gates only.
\[F (A, B, C, D)= \sum (0,2,3,7,8,9) + \sum_{\phi} (1, 10, 11, 12, 13, 14, 15)\]
The K-map is drawn for the given function, and encircling of the groups is done as shown in figure.
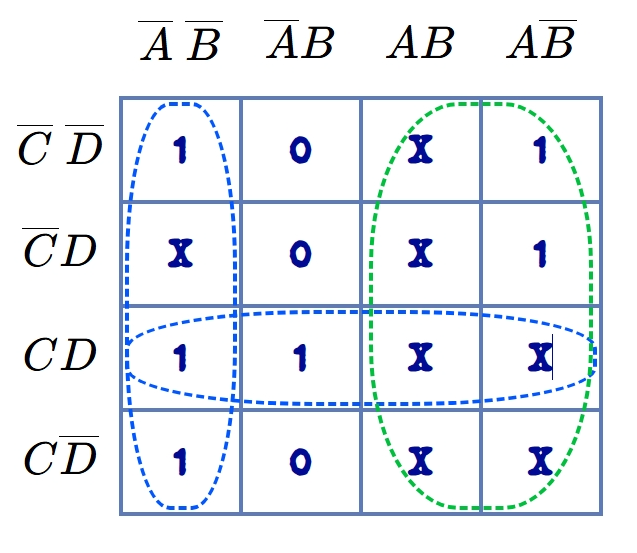
The minimal Boolean function of this K-map is given by:
\[Y = A + CD + \overline{A}~\overline{B}\]