Binary Addition
The addition of two binary numbers is performed in exactly the same manner as the addition of decimal numbers. In fact, binary addition is simpler because we have only two digits (\(0\) and \(1\)). When adding binary numbers, the following rules apply :
| Binary Addition | Sum | Carry in to Next position |
|---|---|---|
| 0 + 0 = | 0 | 0 |
| 1 + 0 = | 1 | 0 |
| 1 + 1 = | 0 | 1 |
| 1 + 1 + 1 = | 1 | 1 |
It is not necessary to consider the addition of more than two binary numbers at a time. It is because the circuitry that actually performs the addition in a digital system can handle only two numbers at a time. When more than two numbers are to be added, the first two are added together, and then their sum is added to the third number, and so on.
Let us illustrate binary addition with few examples.
- (i) Add the following two binary numbers :
1 0 1
+ 0 1 0
-----------
1 1 1
===========The addition is done column by column, starting at the right, as it is in the decimal number system. For the first column, 1 + 0 = 1, and for the second column, 0 + 1 = 1. For the third or last column, 1 + 0 = 1. This produces a sum of 111.
- (ii) Add the following two binary numbers :
1 0 1 1 1
+ 1 0 0 1 0
---------------
1 0 1 0 0 1
===============For the first column, 1 + 0 = 1. In the second column, we have 1 + 1 = 10 = 0 with a carry of 1. For the third column, we have, 1 + 0 + carry of 1 = 1 + 1 = 10 = 0 with a carry of 1. For the fourth column, 1 + 0 + 0 = 1 + 0 = 1. For the fifth column, we have 1 + 1 = 10 = 0 with a carry of 1. This produces a sum of 101001.
Binary addition is the most important arithmetic operation in digital systems. This is because the operations of subtraction, multiplication, and division, as they are performed in most modern digital computers and calculators, actually rely on addition as their fundamental operation.
Subtraction by Addition
Decimal Number
9's Complement method
The 9's complement of a decimal number is a mathematical operation that involves replacing each digit with its complement to 9. This operation is commonly used in computer science and digital arithmetic. The 9's complement operation is often used in digital arithmetic for subtraction operations, which involve adding the complement of the number.
To find the 9's complement of a decimal number, follow these steps:
- Subtract each digit from 9.
- Write down the results of the subtractions as the digits of the 9's complement.
A few examples of finding the 9's complement of decimal numbers are given below:
Now, find the 9's complement of the number = 12345
- Step 1: Subtract each digit from 9
9 - 1 = 8
9 - 2 = 7
9 - 3 = 6
9 - 4 = 5
9 - 5 = 4- Step 2: Write down the results:
9's Complement of 12345 is 87654
Now, find the 9's complement of the number = 9876
- Step 1: Subtract each digit from 9
9 - 9 = 0
9 - 8 = 1
9 - 7 = 2
9 - 6 = 3- Step 2: Write down the results:
9's Complement of 9876 is 123
Now, find the 9's complement of the number = 555
9 - 5 = 4
9 - 5 = 4
9 - 5 = 4The 9's Complement of 555 is 444
9's Complement Subtraction
9’s complement subtraction turns subtraction into addition, with carry handling deciding the sign. The subtraction using the 9’s complement method is done by the following method:
- Write the minuend (the number from which you subtract).
- Find the 9’s complement of the subtrahend.
- Add the minuend and the 9’s complement of the subtrahend.
- If there is a carry beyond the most significant digit, add it back to the result.
- If there is no carry, take the 9’s complement of the result and mark it negative.
Let us see few examples as given below:
- Subtract 348 from 725
9’s complement of 348
999
− 348
---------
651
========= Now, perform the addition of the minuend and the 9's complement of the subtrahend
725
+ 651
---------
1376
========= Now add the carry (MSB) with the rest of the digits
376
+ 1
----------
377
==========- Subtract 725 from 348
9’s complement of 725
999
− 725
--------
274
========Now, finding the result:
348
+ 274
---------
622
=========Since no carry is obtained at the MSB, the resulting number is negative. In this case, convert the result (622) to its 9's complement, which is 377, and the final result is -377.
10's Complement method
The 10's complement is a technique used in digital arithmetic to represent negative numbers. It simplifies subtraction by transforming it into addition, allowing both positive and negative numbers to be represented uniformly. It involves finding the complement of a given decimal number with respect to 10. To find the 10's complement of a number, each digit of the number is subtracted from 9.
The following steps are used to find the 10's complement of a decimal number:
- Subtract each digit of the number from 9.
- Add 1 to the result.
A few examples of finding the 10's complement, along with the method of conversion:
Now, find the 10's complement of the number: 325 10's Complement: 675
Method: Subtract each digit from 9:
For the first digit, 9 - 3 = 6.
For the second digit, 9 - 2 = 7.
For the third digit, 9 - 5 = 4.10's Complement: 675
Now, find the 10's complement of the number: 780
Method: Subtract each digit from 9:
For the first digit, 9 - 7 = 2.
For the second digit, 9 - 8 = 1.
For the third digit, 9 - 0 = 9.10's Complement: 220
Now, find the 10's complement of the number: 4562
Method: Subtract each digit from 9:
For the first digit, 9 - 4 = 5.
For the second digit, 9 - 5 = 4.
For the third digit, 9 - 6 = 3.
For the fourth digit, 9 - 2 = 7.10's Complement: 5438
10's Complement Subtraction
10’s complement subtraction is also similar to the 9's complement method, which turns subtraction into addition with a difference in discarding the carry for positive numbers. If no carry is obtained, then the resulting value is a negative number. Hence, the presence or absence of carry decides the sign.
The method of subtraction using 10’s complement is given as follows:
- Write the minuend (the number from which you subtract).
- Find the 10’s complement of the subtrahend.
- Add the minuend and this 10’s complement.
- If there is a carry beyond the most significant digit, discard MSB and the result is positive.
- If there is no carry, take the 10’s complement of the sum, and the resulting number is negative (add a negative sign).
Let us solve few problems using 10's complement subtraction
- Subtract 348 from 725
10’s complement of 348
1000
− 348
---------
652
=========Now add both the values (minuend and 10's complement of subtrahend)
725
+ 652
---------
1377
=========In this case, 1 is obtained as carry, and hence the result is the value after discarding the carry, and the result is a positive value, which is 377.
Let us see another example showing a negative result.
- Subtract 725 from 25
10’s complement of 725
1000
− 725
---------
275
=========Adding both the minuend and 10's complement of the subtrahend, we get
25
+ 275
---------
300
=========The result has no carry; hence, the result is negative. The value is obtained by taking the 10’s complement of 300, which is 700. So, the final result is -700.
Binary Number
1's Complement method
One's complement is a binary number representation where the negative of a number is represented by inverting all the bits (changing 0s to 1s and 1s to 0s) of its binary representation. The one's complement representation is mainly used for binary arithmetic operations on computers. Negative numbers are represented by taking the one's complement of their positive binary counterpart. A few examples of converting decimal numbers to their one's complement representation:
Method of Conversion to 1's complement
- Convert the decimal number to its binary representation.
- Invert all the bits (change 0s to 1s and 1s to 0s) to get the one's complement representation.
Now, find the 1's complement of the number 7
Decimal : 7
Binary : 0111
One's Complement : 1000Now, find the 1's complement of the number -5
Decimal : -5
Binary : 1011 (2's complement representation of 5)
One's Complement : 0100Now, find the 1's complement of the number 0
Decimal : 0
Binary : 0000
One's Complement : 1111Now, find the 1's complement of the number -15
Decimal : -15
Binary : 10001 (2's complement representation of 15)
One's Complement : 011101's Complement Subtraction
The one's complement method is used to subtract binary numbers. In this method, you negate the second number (the subtrahend) by flipping all of its bits (changing 0s to 1s and 1s to 0s) and then add it to the first number (the minuend). The carry-over is required if any overflow occurs to the next higher bit after the addition is performed. If there's a carry-out after adding, you need to add it back to the result. Also, in the final result, ignore any carry-out beyond the leftmost bit.
A few examples of binary subtraction using the one's complement method are given below:
- Subtract 1101 from 10101 (10101 - 1101)
| Minuend | : | 10101 |
| Subtrahend | : | 1101 |
| Find the one's complement of the subtrahend matching the number of bits in the minuend | : | 10010 |
| Add the one's complement to the minuend | : |
1 0 1 0 1
+ 1 0 0 1 0
-------------
0 0 1 1 1
+ 1
-------------
0 1 0 0 0
=============- Subtract 1001 from 11010 (11010 - 1001)
| Minuend | : | 11010 |
| Subtrahend | : | 1001 |
| Find the one's complement of the subtrahend matching the number of bits in the minuend | : 10110 | |
| Add the one's complement to the minuend | : |
1 1 0 1 0
+ 1 0 1 1 0
-------------
1 0 0 0 0
+ 1
-------------
1 0 0 0 1
=============- Subtract 1011 from 11100 (11100 - 1011)
| Minuend | : | 111000 |
| Subtrahend | : | 1011 |
| Find the one's complement of the subtrahend matching the number of bits in the minuend | : | 110100 |
| Add the one's complement to the minuend | : |
1 1 1 0 0 0
+ 1 1 0 1 0 0
---------------
1 0 1 1 0 0
+ 1
---------------
1 0 1 1 0 1
===============- Subtract 11001 from 101110 (101110 - 11001)
| Minuend | : | 101110 |
| Subtrahend | : | 11001 |
| Find the one's complement of the subtrahend | : | 100110 |
| Add the one's complement to the minuend | : |
1 0 1 1 1 0
+ 1 0 0 1 1 0
---------------
0 1 0 1 0 0
+ 1
---------------
0 1 0 1 0 1
===============2's Complement method
Two's complement Two's complement is a method for representing signed integers in binary form. It involves taking the binary representation of a positive integer, inverting its bits (changing 0s to 1s and 1s to 0s), and then adding 1 to the result. The leftmost bit (the most significant bit) is used to indicate the sign of the number when dealing with two's complement. 0 represents a positive number, and 1 represents a negative number. The range of representable values depends on the number of bits used for the representation.
A few examples of converting decimal numbers to their two's complement binary representation are given below:
- Converting -5 to Two's Complement
| Represent 5 in binary | : | 00000101 |
| Invert the bits | : | 11111010 |
| Add 1 | : | 11111011 (two's complement of -5) |
- Converting -12 to Two's Complement
| Represent 12 in binary | : | 00001100 |
| Invert the bits | : | 11110011 |
| Add 1 | : | 11110100 (two's complement of -12) |
- Converting 7 to Two's Complement (positive number)
| Represent 7 in binary | : | 00000111 |
| Pad with leading zeros to maintain the same bit length | : | 00000111 |
| This is already the two's complement of 7 (positive numbers remain the same in two's complement). |
- Converting -128 to Two's Complement
| Represent 128 in binary | : | 10000000 |
| Invert the bits | : | 01111111 |
| Add 1 | : | 10000000 (overflow occurs, wrapping around) |
Two's Complement Subtraction
In digital systems, subtraction is usually performed by adding the 2’s complement of a number. 2’s complement represents negative numbers in binary. Subtraction in 2’s complement is done by adding the complement of the subtrahend to the minuend, and ignoring overflow. This simplifies the hardware design of an arithmetic circuit by converting subtraction into addition, requiring only an adder circuit.
The following are the steps to perform the Two's complement subtraction:
- Take the number to be subtracted (the subtrahend).
- Find its 2’s complement (invert all bits and add 1 to it).
- Add this result to the minuend (the number from which you subtract).
- If there is a carry out of the most significant bit (MSB), discard it. The remaining bits give the correct result.
A few examples of Two's complement subtraction is given:
- Subtract 10101 from 11001.
Two's complement of 10101 : 01010 + 00001 = 01011
Add the two's complement of the subtrahend to the minuend:
1 1 0 0 1 (minuend)
+ 0 1 0 1 1 (two's complement of subtrahend)
------------
0 0 1 0 0
============The result is 00100 in binary, which is 4 in decimal.
- Subtract 1110 from 10011.
Two's complement of 1110 : 10001 + 00001 = 10010.
Add the two's complement of the subtrahend to the minuend:
1 0 0 1 1
+ 1 0 0 1 0
--------------
1 0 0 1 0 1
============== The result is 00101 in binary, which is 5 in decimal.
Electronic Adders
A logic circuit that performs the function of binary addition is called an electronic adder or an adder. The adder circuit consists of properly connected logic gates. There are usually two forms of the adder in common applications, viz., (i) half adder, (ii) full adder.
Half Adder (HA).
A logic circuit that can add two binary bits is called a half adder (HA). The adder circuit would need two inputs and two outputs. The two inputs are for the two digits to be added, either 0 or 1. One output terminal is for the sum of the two inputs, and the other output is for the carry, if necessary. Fig. 1 shows the truth table of the Half adder.
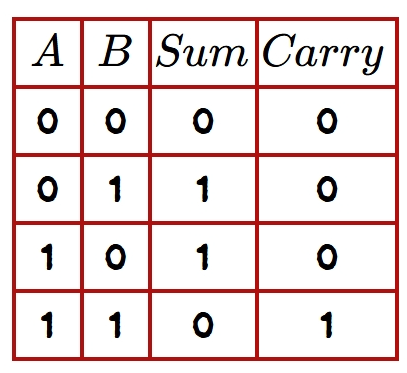
The numbers being added are on the input side of the table. The truth table has two output columns: one for the Sum and one for the Carry. Thus, the half-adder circuit has two inputs (A and B) and two outputs (Sum and Carry).
- (a) The sum column is the output of the XOR gate. The XOR gate has a HIGH output when either input is HIGH, but not when both inputs are HIGH.
- (b) The carry column is the output of the AND gate. Both inputs must be HIGH for there to be a HIGH in the output.
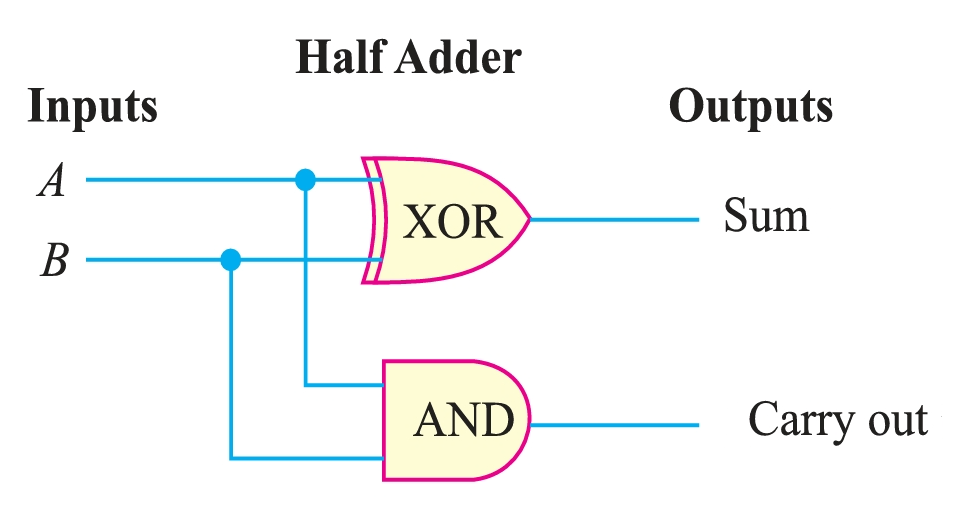
Thus, we can produce a half adder using a two-input AND gate and a two-input XOR gate as shown in Fig. 2. The half adder circuit adds only the LSB column (1s column) in a binary addition problem. The reason is that it has no input for a carry-in.
\[\text{Sum } = \overline{A}B + A\overline{B}\]
\[\text{Carry } = A\cdot B\]
\[\\ \\ or \\ \\\]
\[\text{Sub } = A \oplus B\]
\[C_{in} = A\cdot B\]
Full Adder (FA).
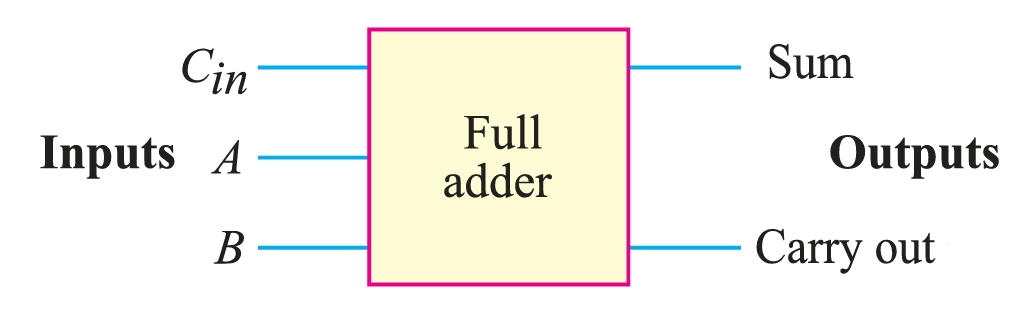
A full adder adds two binary bits plus a carry input (Cin) to produce the Sum and Carry outputs. The full adder is used for binary addition in all places except the 1's place, which corresponds to powers of 2, such as 2s, 4s, 8s, etc. The full adder has three inputs: Cin, A, and B. These three inputs must be added to get the Sum and Carry outputs. Fig. 4 shows the truth table for a full adder, which shows all the possible combinations of A, B, and Cin.
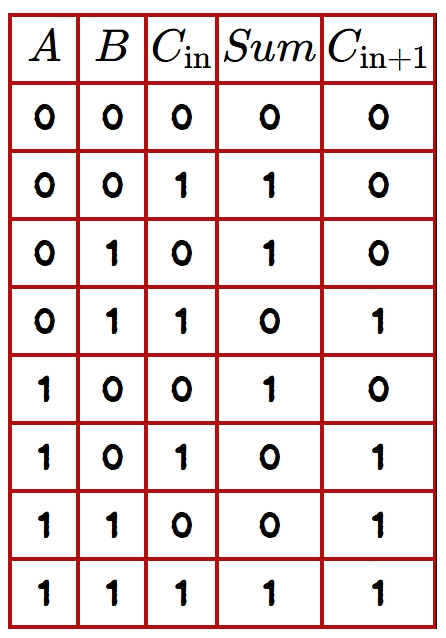
From the truth table, the Boolean expression for the \(Sum\) and \(Carry\) of a Full adder is given below:
\[\text{Sum } = (\overline{A}B + A\overline{B})\overline{C_{in}} + \overline{(\overline{A}B + A\overline{B})}C_{in}\]
\[\text{Carry } = AB + (\overline{A}B + A\overline{B})C_{in}\]
\[\\ \\ or \\ \\ \]
\[\text{Sum } = A \oplus B \oplus C_{in}\]
\[\text{Carry } = AB + (A \oplus B)\cdot C_{in}\]
A full adder is formed by using two half adder circuits and an OR gate, as shown in Fig. 5. Note the carry-in input, which necessitates the addition of an extra half adder. The output of the OR gate forms the carry-out output. Fig. 6 shows the block diagram of a full adder.
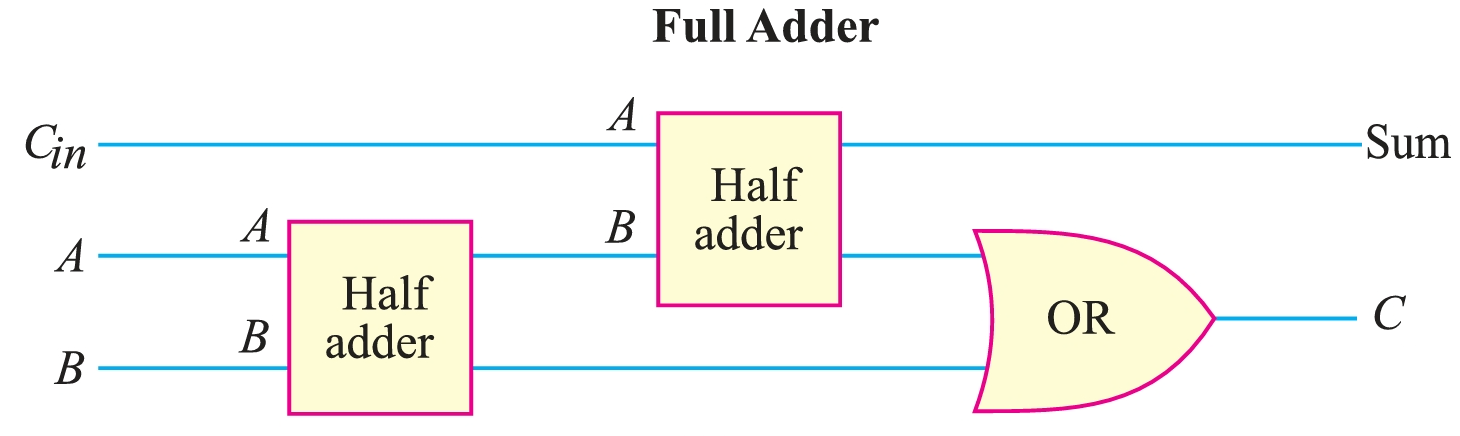
Half Subtractor (HS).
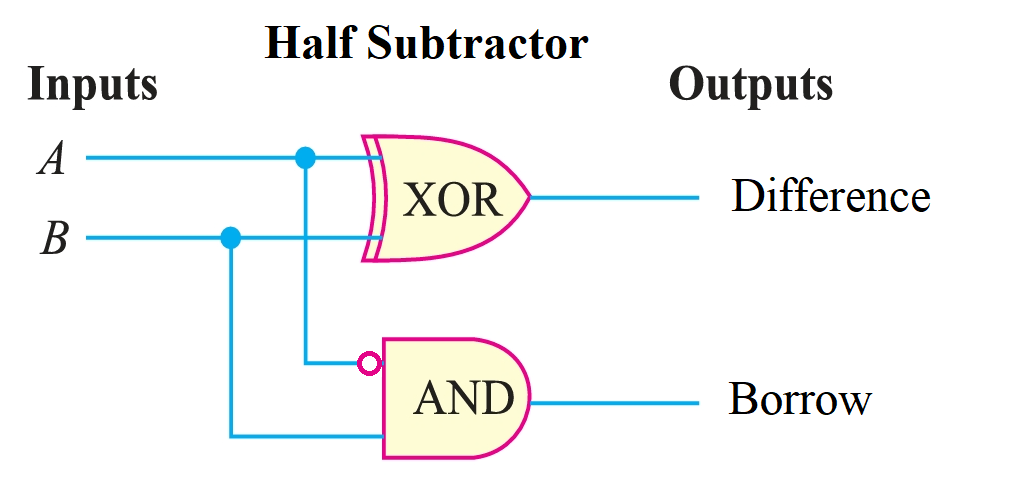
One of the fundamental operations in digital electronics is subtraction, which is essential for arithmetic and logic operations. A half subtractor is a combinational logic circuit that performs the subtraction of two binary digits, providing both the difference and borrow outputs. In this article, we will delve into the working principles, circuit design, truth table, and applications of a half subtractor.
A half subtractor is designed to subtract two single binary digits, often referred to as the minuend \(A\) and the subtrahend \(B\), producing two outputs: the difference \(D\) or \(Sub\) and the borrow \(Borrow\). The borrow output indicates whether a borrow is required during subtraction.
The truth table of a half subtractor lists all possible input combinations and their corresponding outputs. There are four possible input combinations for a half subtractor:
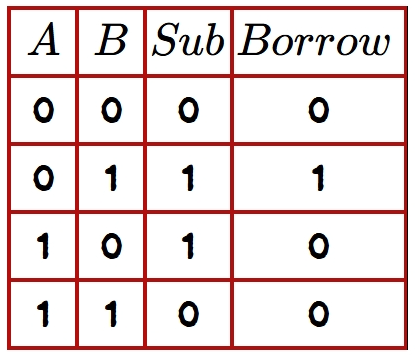
From the truth table, we can derive the logic equations for the difference (D) and borrow (Bout) outputs:
\[\text{Difference, } Sub = \overline{A}B + A\overline{B}\]
\[\text{Borrow, } (B_{out}) = \overline{A}B\]
\[\\ \\ or \\ \\\]
\[\text{Sub } = A \oplus B\]
\[B_{out} = \overline{A}B\]
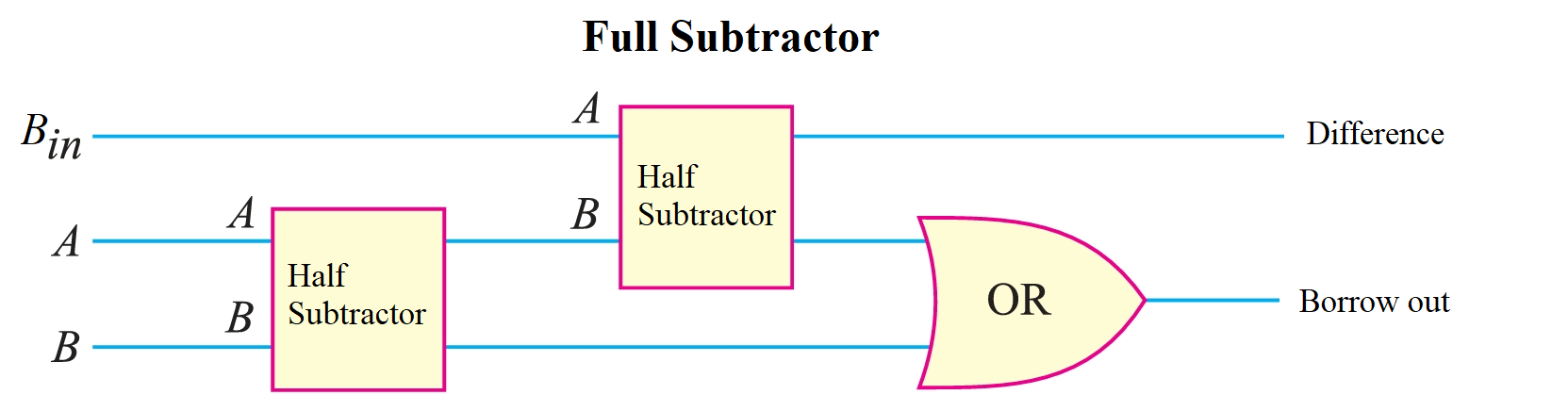
Full Subtractor (FS).
Full subtractor is a combinational circuit used to subtract three binary digits, taking into account the borrow from the previous stage.
A full subtractor is a logical circuit that takes three binary inputs: the minuend \(A\), the subtrahend \(B\), and a borrow input \(B_{in}\). It produces two outputs: the difference \(Diff\) and a borrow output \(B_{out}\). The borrow input \(B_{in}\) is the carry generated by the subtraction of the previous stage. The full subtractor circuit is crucial for performing binary subtraction in multi-bit systems.
The truth table for a full subtractor outlines all possible combinations of inputs and their corresponding outputs. Considering the inputs \(A\), \(B\), and \(B_{in}\), and the outputs \(Diff\) and \(B_{out}\), the truth table for a full subtractor is as follows:
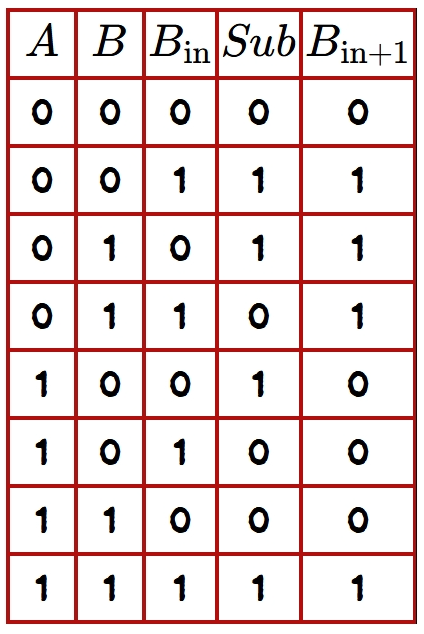
In the truth table, each row corresponds to a unique combination of input values, and the corresponding outputs \(Diff\) and \(B_{out}\) are provided. This table encapsulates the full subtractor's behavior in response to various input scenarios.
From the truth table, the Boolean expression for the \(Sub\) and \(Borrow\) of a Full adder is given below:
\[\text{Sub } = (\overline{A}B + A\overline{B})\cdot \overline{B_{in}} + \overline{(\overline{A}B + A\overline{B})}\cdot B_{in}\]
\[B_{out} = \overline{A}B + (\overline{A}B + A\overline{B})\cdot\overline{B_{in}}\]
\[\\ \\ or \\ \\\]
\[\text{Sub} = A \oplus B \oplus B_{in}\]
\[B_{out} = AB + (A \oplus B)\cdot \overline{B_{in}}\]
Binary Adder-Subtractor
The binary adder-subtractor circuit is a crucial building block in digital systems, enabling both addition and subtraction operations within a single integrated circuit.
A binary adder-subtractor circuit combines the functionalities of an adder and a subtractor into a single unit, allowing for versatile computation. This circuit is designed to handle two binary numbers, performing either addition or subtraction operations based on control inputs.
The binary adder-subtractor circuit performs two primary operations: addition and subtraction. It is equipped with a control input that determines whether the circuit should perform an addition or subtraction operation. This control input is typically denoted as the "subtract" or "Borrow-In" (\(B_{in}\)) signal. When the \(B_{in}\) signal is set to 0, the circuit performs an addition, and when it is set to 1, the circuit performs subtraction.
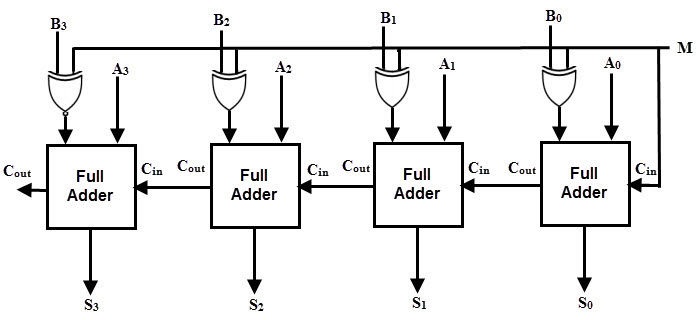
Binary addition involves the process of adding two binary numbers, similar to conventional decimal addition. The binary adder-subtractor circuit performs this operation by considering individual bits of the numbers along with a carry input. The circuit follows a cascading structure, where each stage handles a pair of bits from the input numbers along with the carry generated by the previous stage.
The operation at each stage includes three inputs: \(A\), \(B\), and the carry from the previous stage (\(C_{in}\)), and two outputs: the sum (\(S\)) and the carry-out (\(C_{out}\)) for the next stage.
The sum (\(S\)) at each stage is computed using the XOR gate, while the carry-out (\(C_{out}\)) is determined using the AND and XOR gates. The carry-in (\(C_{in}\)) for the least significant bit (LSB) stage is typically set to 0. The carry-out from the most significant bit (MSB) stage is considered the final carry-out of the entire addition operation.
Binary subtraction, when performed manually, involves borrowing from higher-order bits to perform the subtraction of lower-order bits. The binary adder-subtractor circuit automates this process using the control input \(B_{in}\). When the \(B_{in}\) input is set to 1, the circuit performs subtraction. To achieve this, the two's complement method is utilized. The two's complement of a binary number is obtained by inverting its bits (changing 0s to 1s and vice versa) and adding 1 to the result.
When subtracting a binary number \(B\) from another binary number \(A\), the circuit computes the sum of \(A\) and the two's complement of \(B\). By using the two's complement, subtraction is transformed into addition, which can be handled by the same binary adder circuit. The final output is then corrected by discarding the carry-out from the MSB stage and considering it as an overflow indicator.