Maximum Power Transfer Theorem
When load is connected across a voltage source, power is transferred from the source to the load. The amount of power transferred will depend upon the load resistance. If load resistance \(R_{L}\) is made equal to the internal resistance \(R_{i}\) of the source, then maximum power is transferred to the load \(R_{L}\). This is known as maximum power transfer theorem and can be stated as follows :
Maximum power is transferred from a source to a load when the load resistance is made equal to the internal resistance of the source.
This applies to d.c. as well as a.c. power. To prove this theorem mathematically, consider a voltage source of generated voltage \(E\) and internal resistance \(R_{i}\) and delivering power to a load resistance \(R_{L}\). The current \(I\) flowing through the circuit is given by :
\[I = \frac{E}{R_{L}+R_{i}}\]
\[\text{Power delivered to load, } P = I^{2}R_{L} = \left(\frac{E}{R_{L}+R_{i}}\right)^{2}R_{L}\]
For a given source, generated voltage \(E\) and internal resistance \(R_{i}\) are constant. Therefore, power delivered to the load depends upon \(R_{L}\). In order to find the value of \(R_{L}\) for which the value of \(P\) is maximum, it is necessary to differentiate eq. (i) w.r.t. \(R_{L}\) and set the result equal to zero.
\[\frac{P}{R_{L}} = E^{2}\left[\frac{(R_{L}+R_{i})^{2}-2R_{L}(R_{L}+R_{i})}{(R_{L}+R_{i})^{4}}\right] =0\]
\[(R_{L}+R_{i})^{2}-2R_{L}(R_{L}+R_{i}) =0\ (R_{L}+R_{i}-2R_{L})=0\ (R_{i}-R_{L})=0\ R_{i}=R_{L}\]
i.e Load resistance = Internal resistance
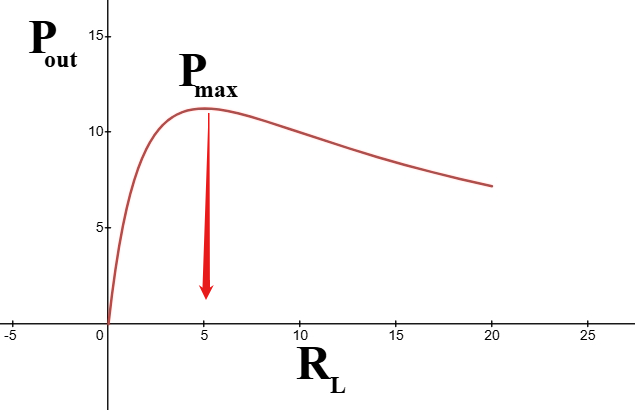
Thus, for maximum power transfer, load resistance \(R_{L}\) must be equal to the internal resistance \(R_{i}\) of the source. Under such conditions, the load is said to be matched to the source. Fig. 2 shows a graph of power delivered to \(R_{L}\) as a function of \(R_{L}\). It may be mentioned that efficiency of maximum power transfer is 50 % as one-half of the total generated power is dissipated in the internal resistance \(R_{i}\) of the source.
| Efficiency | = | \(\frac{\text{output power}}{\text{input power}} = \frac{I^{2}R_{L}}{I^{2}(R_{L}+R_{i})}\) |
| = | \(\frac{R_{L}}{2R_{L}} = \frac{1}{2} = 50 %\) |
Electric power systems never operate for maximum power transfer because of low efficiency and high voltage drops between generated voltage and load. However, in the electronic circuits, maximum power transfer is usually desirable. For instance, in a public address system, it is desirable to have load (i.e. speaker) matched to the amplifier so that there is maximum transference of power from the amplifier to the speaker. In such situations, efficiency is sacrificed at the cost of high power transfer.
Let us consider a generator develops 200 V and has an internal resistance of 100 Ω. The estimate of power transfer at various load are given in the table 1.
| \(R_{L} ~ (\Omega)\) | Load Current, \(I = \frac{E}{R_{L}+R_{i}}\) | Power delivered to \(R_{L}\), \(I^{2}R_{L}\) | Total Power, \(I^{2}(R_{L}+R_{i})\) | Efficiency (%) |
|---|---|---|---|---|
| \(100\) | \(\frac{200}{100+100}= 1.00 A\) | \((1.00)^{2} \times 100 = 100 ~watts\) | \(200 ~watts\) | \(50\) |
| \(200\) | \(\frac{200}{200+100}= 0.66 A\) | \((0.66)^{2} \times 200 = 88.8 ~watts\) | \(133.33 ~watts\) | \(66.60\) |
| \(200\) | \(\frac{200}{300+100}= 0.50 A\) | \((0.50)^{2} \times 300 = 75 ~watts\) | \(100 ~watts\) | \(75\) |
It is clear from the table 1 that although in case of \(R_{L} = R_{i}\), a large power (\(100 ~W\)) is transferred to the load, but there is a big wastage of power in the generator. On the other hand, when \(R_{L}\) is not equal to \(R_{i}\), the power transfer is less (\(75 ~W\)) but smaller part is wasted in the generator i.e., efficiency is high. Thus, it depends upon a particular situation as to what the load should be. If we want to transfer maximum power (e.g. in amplifiers) irrespective of efficiency, we should make \(R_{L} = R_{i}\). However, if efficiency is more important (e.g. in power systems), then internal resistance of the source should be consider ably smaller than the load resistance.