The superposition theorem
Sometimes it is helpful to consider separately the effects of sources on a particular part of the circuit; the superposition theorem lets us do that. It states
The current in any branch of a circuit, or the voltage at any node, may be found by the algebraic addition of the currents or voltages produced by each source separately. When the effect of one source is being considered, the other sources are replaced by their internal resistances.
Superposition is most useful when the sources are alternating sources of differing frequency, or a combination of direct and alternating sources, but we can illustrate the use of superposition with direct sources alone.
Consider the circuit of figure once more in which we wish to find \(V_{AB}\) using superposition. For this we must add the voltages produced across \(AB\) by each source in turn.
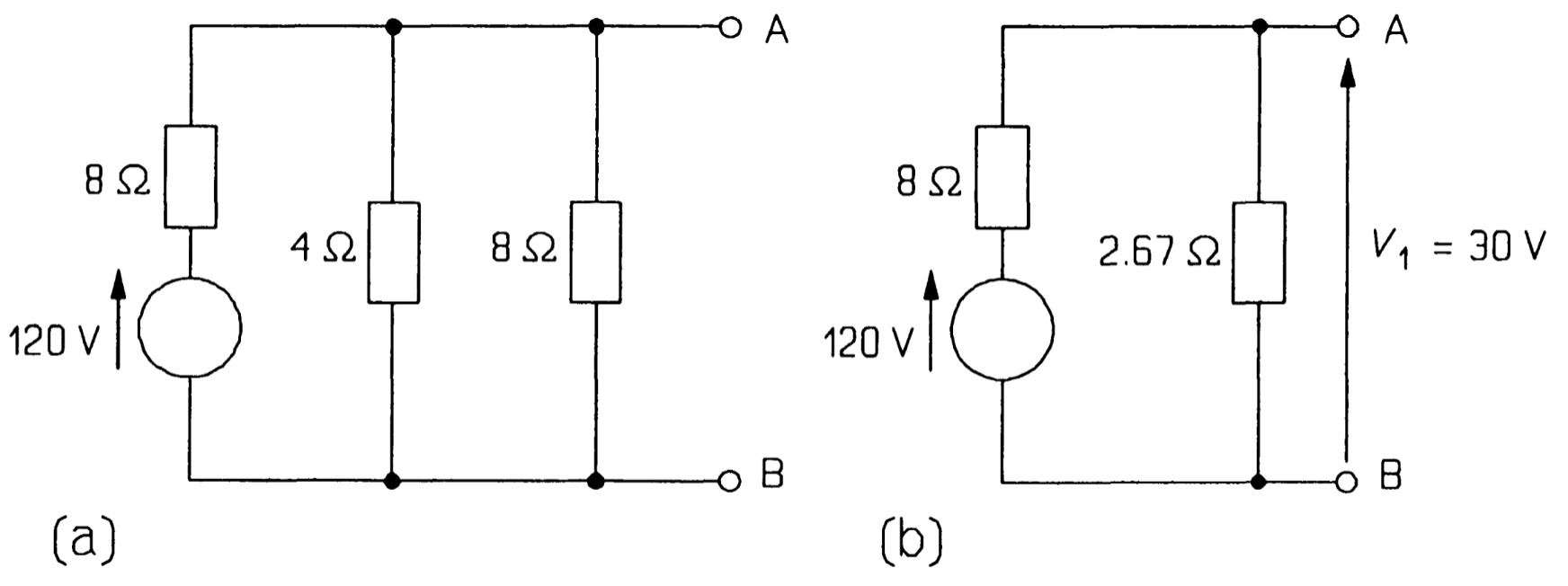
Taking the 120 V source first, we replace the other voltage sources by short circuits to obtain the circuit in figure. The parallel \(4~\Omega\) and \(8~\Omega\) resistances may be combined to give one of \(2.67~\Omega\), which is in series with the remaining 80 resistance, for a total resistance of \(10.67~\Omega\), so V, by the voltage divider rule must be \((2.67 /10.67) \times 120 = 30\) \(V\), as in figure
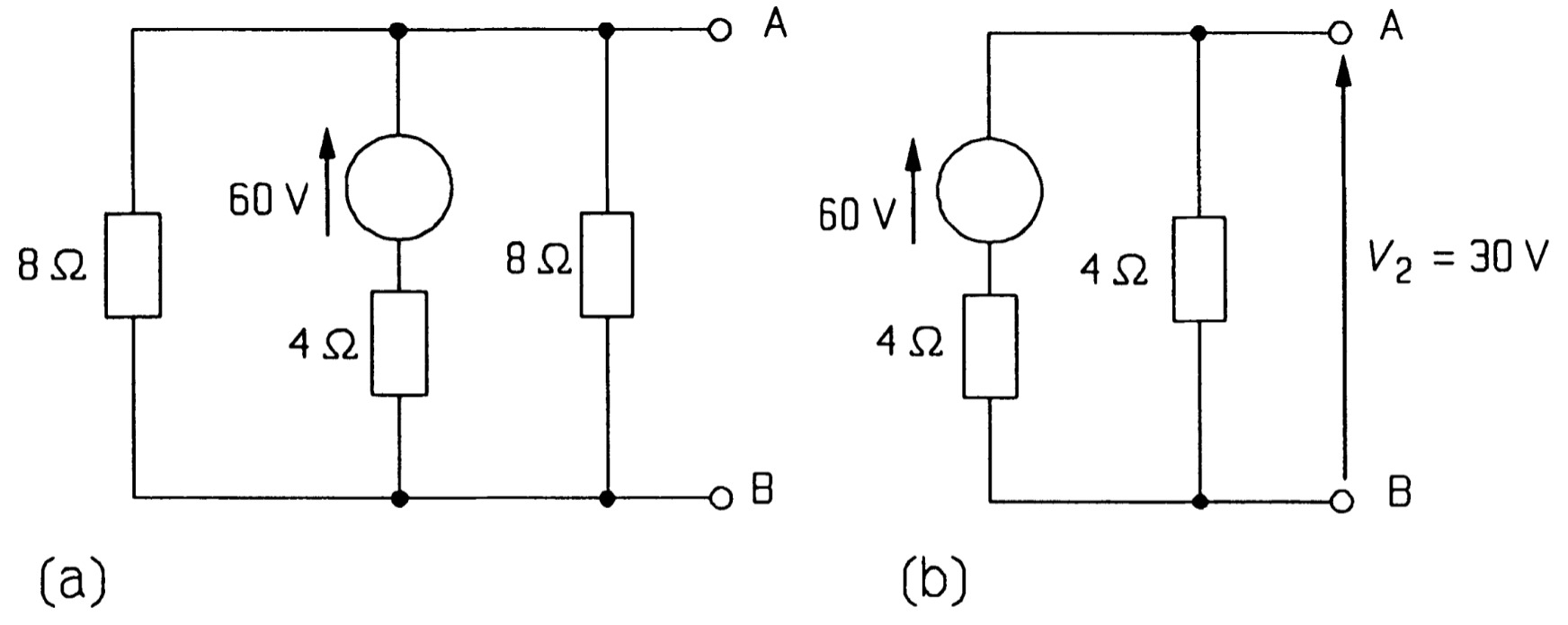
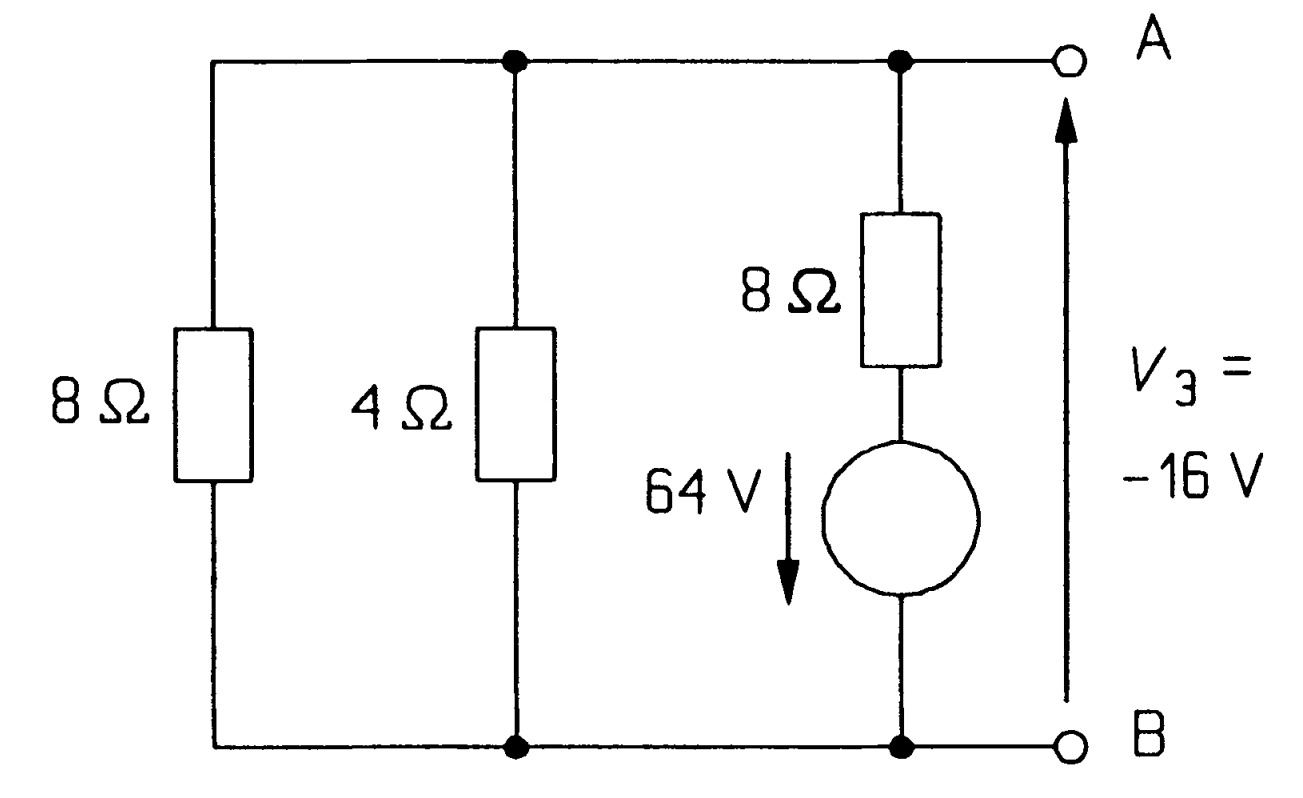
Proceeding in the same way to examine the effect of the 60V source we 'kill' the other two sources by replacing them with short circuits as in figure. The two \(8~\Omega\) resistances are in parallel as far as the \(60 V\) source is concerned, so they may be combined into a \(4~\Omega\) resistance. This is in series with the \(4~\Omega\) resistance next to the source, as in figure, so the voltage divider rule gives \(V_2\) as 30 V. The last step is to look at the effect of the 64 V source, as in figure. \(V_3\), the required voltage, is that across the parallel combination of \(8 ~\Omega\) and \(4~\Omega\) resistances, but as the 64 V source points to Band not A like the other two, \(V_3\) must be negative. Once again the parallel resistances combine to give one of \(2.67~\Omega\), so \(V_3\), calculated by the voltage divider rule, is
\[(2.67/10.67) \times (-64) V = -16 V\]
Summing:
\[V_{AB} = V_{1}+V_{2}+V_{3}\]