Effect of Temperature
The electrical conductivity of a semiconductor changes appreciably with temperature variations.
At absolute zero.
At absolute zero temperature, all the electrons are tightly held by the semiconductor atoms. The inner orbit electrons are bound, whereas the valence electrons are engaged in covalent bonding. At this temperature, the covalent bonds are very strong, and there are no free electrons. Therefore, the semiconductor crystal behaves as a perfect insulator.
In terms of energy band description, the valence band is filled, and a large energy gap exists between the valence band and the conduction band. Therefore, no valence electron can reach the conduction band to become a free electron. It is due to the non-availability of free electrons that a semiconductor behaves as an insulator.
Above absolute zero.
When the temperature is raised, some of the covalent bonds in the semiconductor break due to the thermal energy supplied. The breaking of bonds sets those electrons free that are engaged in the formation of these bonds. The result is that a few free electrons exist in the semiconductor. These free electrons can constitute a tiny electric current if a potential difference is applied across the semiconductor crystal. This indicates that the resistance of a semiconductor decreases with an increase in temperature, i.e., it has a negative temperature coefficient of resistance. It may be added that at room temperature, current through a semiconductor is too small to be of any practical value.
As the temperature is raised, some of the valence electrons acquire sufficient energy to enter the conduction band and thus become free electrons. Under the influence of an electric field, these free electrons will constitute an electric current. It may be noted that each time a valence electron enters the conduction band, a hole is created in the valence band. The holes also contribute to the current.
At room temperature, some of the covalent bonds in pure semiconductor break, setting up free electrons. Under the influence of an electric field, these free electrons constitute an electric current. At the same time, another current – the hole current – also flows in the semiconductor. When a covalent bond is broken due to thermal energy, the removal of one electron leaves a vacancy, i.e., a missing electron in the covalent bond. This missing electron is called a hole, which acts as a positive charge. Hole acts as a virtual charge, although there is no physical charge on it.
For one electron set free, one hole is created. Therefore, thermal energy creates hole-electron pairs; there are as many holes as the free electrons. The current conduction by holes can be explained as follows :
When the valence electron becomes a free electron due to thermal energy, it creates a hole in the covalent bond of the atom. The hole is a strong centre of attraction for the electron. A valence electron from a nearby covalent bond comes to fill in the hole. This results in the creation of a hole at the neighbouring location from where the electron came. Another valence electron, in turn, may leave its bond to fill the previous hole, thus creating a new hole. Thus, the hole with a positive charge has moved from one location in the solid to another, i.e., towards the negative terminal of the supply. This constitutes the Hole current. Hole current is due to the movement of valence electrons from one covalent bond to another bond.
The temperature dependence of the resistivity of semiconductors and insulators is given by the following formula :-
\[\rho(T) = \rho_0~e^{-\frac{E_g}{k_B T}}\]
where, \(E_g\) is the energy gap between conduction band and valance band, \(k_B\) is the Boltzmann's constant, \(T\) is the temperature and \(\rho(T)\) and \(\rho_0\) is the resistivity of the material as temperature T (in Kelvin) and at zero Kelvin, respectively.
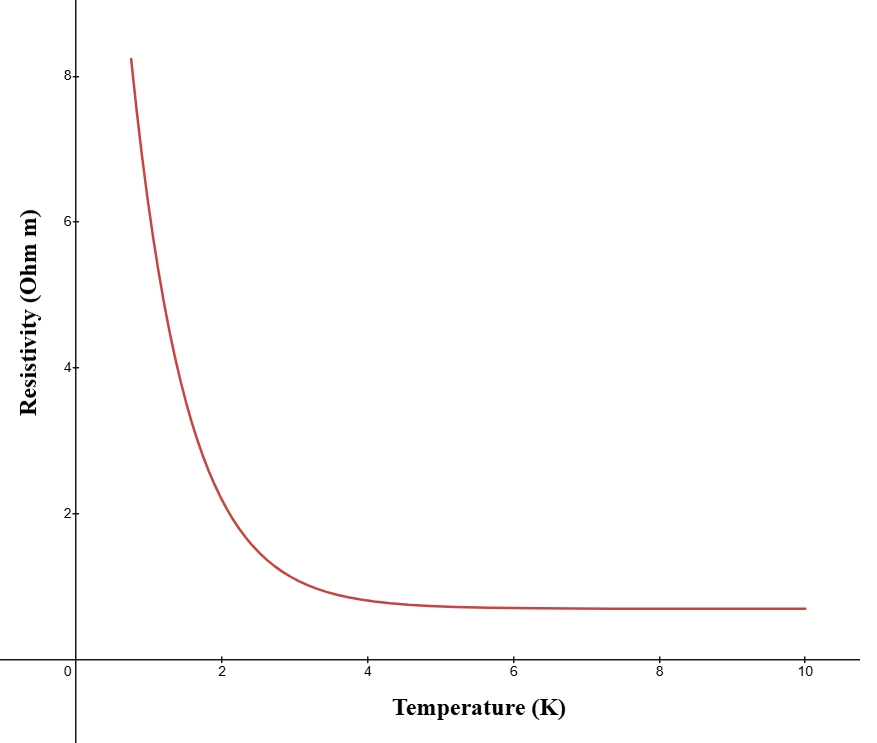
The resistivity of insulators increases exponentially as the temperature decreases. At absolute zero the resistivity of insulators becomes infinite, that is, at 0K the conductivity of insulators becomes almost zero.
