Number Systems

Number Systems

The language we use to communicate with each other is comprised of words and characters. We understand numbers, characters and words. But this type of data is not suitable for computers. Computers only understand the numbers. So, when we enter data, the data is converted into the electronic pulse. Each pulse is identified as code and the code is converted into numeric format by ASCII. It gives each number, character and symbol a numeric value (number) that a computer understands. So, to understand the language of computers, one must be familiar with the number systems.

The number system or the numeral system is the system of naming or representing numbers. We know that a number is a mathematical value that helps to count or measure objects and it helps in performing various mathematical calculations. There are different types of number systems in Maths like decimal number system, binary number system, octal number system, and hexadecimal number system. In this article, we are going to learn what is a number system in Maths, different types, and conversion procedures with many number system examples in detail.

What is Number System in Maths?

A number system is defined as a system of writing to express numbers. It is the mathematical notation for representing numbers of a given set by using digits or other symbols in a consistent manner. It provides a unique representation of every number and represents the arithmetic and algebraic structure of the figures. It also allows us to operate arithmetic operations like addition, subtraction, multiplication and division.

The value of any digit in a number can be determined by:

  1. The digit
  2. Its position in the number
  3. The base of the number system

Before discussing the different types of number system examples, first, let us discuss what is a number?

What is a Number?

A number is a mathematical value used for counting or measuring or labelling objects. Numbers are used to performing arithmetic calculations. Examples of numbers are natural numbers, whole numbers, rational and irrational numbers, etc. 0 is also a number that represents a null value.

A number has many other variations such as even and odd numbers, prime and composite numbers. Even and odd terms are used when a number is divisible by 2 or not, whereas prime and composite differentiate between the numbers that have only two factors and more than two factors, respectively.

In a number system, these numbers are used as digits. 0 and 1 are the most common digits in the number system, that are used to represent binary numbers. On the other hand, 0 to 9 digits are also used for other number systems. Let us learn here the types of number systems.

Types of Number Systems

There are various types of number systems in mathematics. The four most common number system types are:

  1. Decimal number system (Base - 10)
  2. Binary number system (Base - 2)
  3. Octal number system (Base - 8)
  4. Hexadecimal number system (Base - 16)

Now, let us discuss the different types of number systems with examples.

Decimal Number System (Base 10 Number System)

The decimal number system has a base of 10 because it uses ten digits from 0 to 9. In the decimal number system, the positions successive to the left of the decimal point represent units, tens, hundreds, thousands and so on. This system is expressed in decimal numbers. Every position shows a particular power of the base (10).

Example of Decimal Number System:

The decimal number 1457 consists of the digit 7 in the units position, 5 in the tens place, 4 in the hundreds position, and 1 in the thousands place whose value can be written as:

(1×103) + (4×102) + (5×101) + (7×100)

(1×1000) + (4×100) + (5×10) + (7×1)

1000 + 400 + 50 + 7

1457
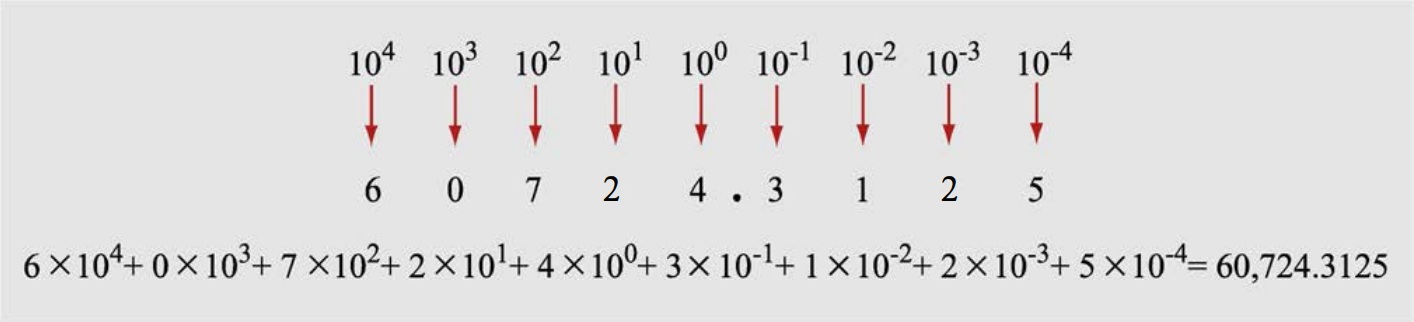
Decimal number representation
Decimal number representation

Binary Number System (Base 2 Number System)

The base 2 number system is also known as the Binary number system wherein, only two binary digits exist, i.e., 0 and 1. Specifically, the usual base-2 is a radix of 2. The figures described under this system are known as binary numbers which are the combination of 0 and 1. For example, 110101 is a binary number.

Binary number representation
Binary number representation

We can convert any system into binary and vice versa.

Example

Write (14)10 as a binary number.

Solution:

Base 2 Number System Example ∴ (14)10 = 11102

Octal Number System (Base 8 Number System)

In the octal number system, the base is 8 and it uses numbers from 0 to 7 to represent numbers. Octal numbers are commonly used in computer applications. Converting an octal number to decimal is the same as decimal conversion and is explained below using an example.

Example: Convert 2158 into decimal.

Solution:

2158 = 2 × 82 + 1 × 81 + 5 × 80

= 2 × 64 + 1 × 8 + 5 × 1

= 128 + 8 + 5

= 14110

Hexadecimal Number System (Base 16 Number System)

In the hexadecimal system, numbers are written or represented with base 16. In the hexadecimal system, the numbers are first represented just like in the decimal system, i.e. from 0 to 9. Then, the numbers are represented using the alphabet from A to F. The below-given table shows the representation of numbers in the hexadecimal number system.

Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F
Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Number System Conversion

Numbers can be represented in any of the number system categories like binary, decimal, hexadecimal, etc. Also, any number which is represented in any of the number system types can be easily converted to another. Check the detailed lesson on the conversions of number systems to learn how to convert numbers in decimal to binary and vice versa, hexadecimal to binary and vice versa, and octal to binary and vice versa using various examples.

With the help of the different conversion procedures explained above, now let us discuss in brief about the conversion of one number system to the other number system by taking a random number.

Assume the number 349. Thus, the number 349 in different number systems is as follows:

Number System Solved Examples

Example 1:Convert (1056)16 to an octal number.

Solution:

Given, 105616 is a hex number.

First we need to convert the given hexadecimal number into decimal number 

(1056)16

= 1 × 163 + 0 × 162 + 5 × 161 + 6 × 160

= 4096 + 0 + 80 + 6

= (4182)10

Now we will convert this decimal number to the required octal number by repetitively dividing by 8.

8 4182 Remainder
8 522 6
8 65 2
8 8 1
8 1 0
0 1

Therefore, taking the value of the remainder from bottom to top, we get;

(4182)10 = (10126)8
Therefore,
(1056)16 = (10126)8

Example 2: Convert (1001001100)2 to a decimal number.

Solution:

(1001001100)2

= 1 × 29 + 0 × 28 + 0 × 27 + 1 × 26 + 0 × 25 + 0 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20

= 512 + 64 + 8 + 4

= (588)10

Example 3: Convert 101012 into an octal number.

Solution:

Given,

101012 is the binary number

We can write the given binary number as,

010 101

Now as we know, in the octal number system,

010 → 2
101 → 5

Therefore, the required octal number is (25)8

Example 4: Convert hexadecimal 2C to decimal number.

Solution:

We need to convert 2C16 into binary numbers first.

2C → 00101100

Now convert 001011002 into a decimal number.

101100 = 1 × 25 + 0 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20

= 32 + 8 + 4

= 44

Number System Questions

  1. Convert (242)10 into hexadecimal. [Answer: (F2)16]
  2. Convert 0.52 into an octal number. [Answer: 4121]
  3. Subtract 11012 and 10102. [Answer: 0010]
  4. Represent 5C616 in decimal. [Answer: 1478]
  5. Represent binary number 1.1 in decimal. [Answer: 1.5]

Computer Numeral System (Number System in Computers)

When we type any letter or word, the computer translates them into numbers since computers can understand only numbers. A computer can understand only a few symbols called digits and these symbols describe different values depending on the position they hold in the number. In general, the binary number system is used in computers. However, the octal, decimal and hexadecimal systems are also used sometimes.

Floating-point number representation

Floating-point number representation is a fundamental concept in computer science and mathematics, essential for accurately representing real numbers in a digital format. This method allows computers to handle a wide range of numerical values, including both very small and very large numbers, with a compromise between precision and range. The details of floating-point representation, its components, and properties, are provided with few illustrative examples.

Basics of Floating-Point Representation:

Floating-point numbers are expressed in scientific notation as (±m) × 2e, where "m" represents the significand or mantissa, "e" denotes the exponent, and the sign bit indicates the sign of the number. The base, usually 2, is chosen to reflect the binary nature of computers. The IEEE 754 standard is commonly used for floating-point representation, providing single (32-bit) and double (64-bit) precision formats.

To accommodate large and small numbers, real numbers are written in floating point representation. Decimal floating point representation (also called scientific notation) has the form:

Floating Point representation
Floating Point representation

One digit is written to the left of the decimal point, and the rest of the significant digits are written to the right of the decimal point. The number 0.dddddd is called the mantissa. p represents the order of magnitude of the number having the base 10, which is also known as exponent. The first digit is zero for the number starting with a digit smaller than 5. Binary floating point representation has the form: \(1.bbbbbb \times 2^{bbb}\) (\(b\) is a decimal digit).

\noindent For example:

Components of Floating-Point Representation:

Storage of number in Computer memory

The computer stores the values of the exponent and the mantissa separately, while the leading 1 in front of the decimal point is not stored. According to the IEEE-754 standard (1985), computers store numbers and carry out calculations in single precision (32-bit) or in double precision (64-bit). In single precision, the numbers are stored in a string of 32 bits (4 bytes), and in double precision in a string of 64 bits (8 bytes). In both cases the first bit stores the sign (0 corresponds to + and 1 corresponds to -) of the number. The next 8 bits in single precision (11 bits in double precision) are used for storing the exponent. The following 23 bits in single precision (52 bits in double precision) are used for storing the mantissa.

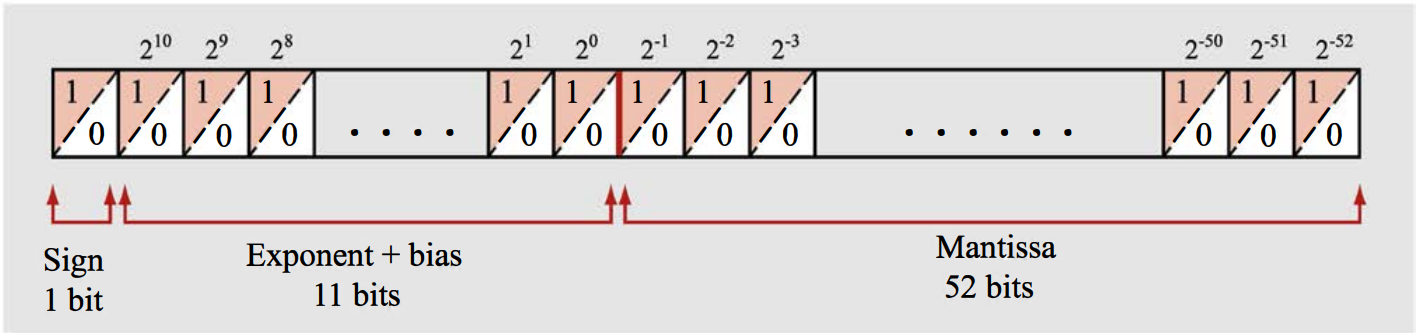
memory
64-bit Memory space

The value of the exponent is entered with a bias. A bias means that a constant is added to the value of the exponent. The bias is introduced in order to avoid using one of the bits for the sign of the exponent (since the exponent can be positive or negative). The smallest and largest values of the exponent plus bias are reserved for zero and infinity (Inf) or not-a-number (NaN}) due to invalid mathematical operation. The 11 bits for the exponent plus bias store values between \(-1023\) and \(1024\). If the exponent plus bias and mantissa are both zero, then the number actually stored is 0. If the exponent plus bias is \(2047\) the number stored is Inf if the mantissa is zero, and it is NaN if the mantissa is not zero. In single precision, \(8\) bits are allocated to the value of the exponent and the bias is \(127\).

Not every number can be accurately written in binary form since a finite number of bits is used. That means, only a finite number of exact values in decimal format can be stored in binary form. For example: \(0.1\) cannot be represented exactly in the finite binary format in the single precision memory space. The irrational numbers cannot be represented exactly in any format. The exact values are approximated. The errors that are introduced are small in one step, but when many operations are executed, the errors can grow to such an extent that the final answer is affected.

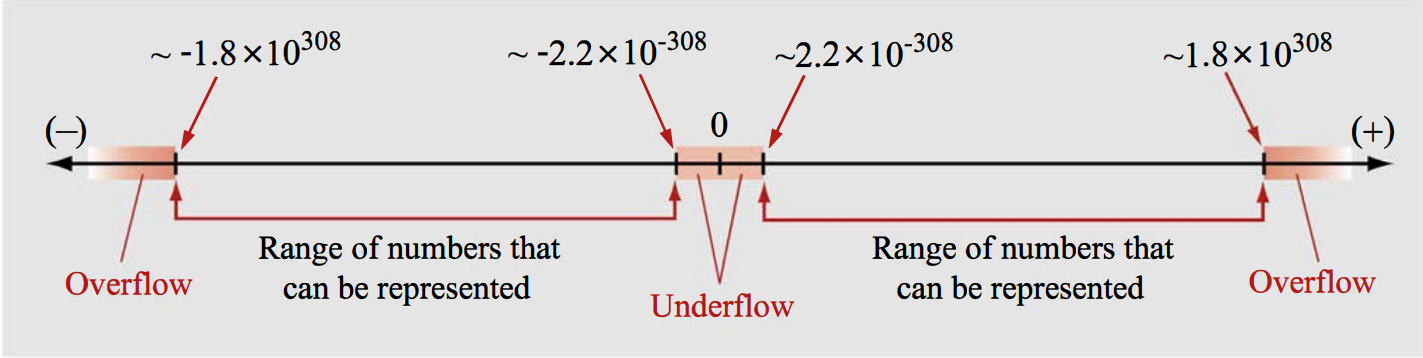
The interval between numbers that can be represented depends on their magnitude. In double precision, the smallest value of the mantissa that can be stored is \(2^{-52} \sim 2.22 \times 10^{-16}\). This is also the smallest possible difference in the mantissa between two numbers.

The smallest positive number that can be expressed in double precision is \(2^{-1022} \sim 2.2 \times 10^{-308}\) and the closest negative number to zero is \(-2.2 \times 10^{-308}\). Any number between \(-2.2 \times 10^{-308}$ and $2.2 \times 10^{-308}\) cannot be stored in memory leading to underflow error.

The largest positive number that can be expressed in double precision is approximately \(2^{1024} \sim 1.8 \times 10^{308}\) and the largest negative number expressed approximately in double precision is \(-2^{1024} \sim -1.8 \times 10^{308}\). Any number larger than \(1.8 \times 10^{308}\) or smaller than \(-1.8 \times 10^{308}\) leads to overflow error.

Data Storage
Data Storage possible in 64-bit memory space

Single Precision vs. Double Precision:

Single precision uses 32 bits with 1 bit for the sign, 8 bits for the exponent, and 23 bits for the significand. Double precision employs 64 bits with 1 bit for the sign, 11 bits for the exponent, and 52 bits for the significand. Double precision offers higher accuracy but requires more memory and computation.

Examples:

Example 1: Representing 123.456 in Single Precision

Decimal: 123.456 = 1.23456 × 102

Binary of 123.456: 1111011.01110100011110101110000101000100001011010001111...

Approximate Single Precision: 1.11101101110100011110101 × 26

Example 2: Representing -0.00123 in Double Precision

Decimal: -0.00123 = -1.23 × 10-3

Binary of 0.00123: 0.00000010000100110111...

Approximate Double Precision: -1.000010010110111... × 2-10

Precision and Accuracy:

Floating-point representation involves a trade-off between precision and range. As the range increases, the precision decreases. Not all decimal numbers can be accurately represented due to the finite number of bits. This can lead to rounding errors and loss of precision in calculations.

Special Cases:

Rounding Errors:

Due to the finite precision of floating-point numbers, rounding errors accumulate in complex calculations. Comparisons of floating-point values should be handled with caution, using an epsilon value for tolerance.

Number System: Exercise

Conversion of binary numbers to decimal numbers

Converting binary numbers to decimal numbers involves understanding the positional notation of both systems. Each digit in a binary number represents a power of 2, just as each digit in a decimal number represents a power of 10.

To perform binary to decimal conversion, follow these steps for each example:

  1. Write down the binary number.
  2. Assign a power of 2 to each digit, starting from 0 for the rightmost digit and increasing by 1 for each subsequent digit.
  3. Multiply each digit by its corresponding power of 2.
  4. Add up all the results from step 3 to obtain the decimal equivalent.

Few examples of binary to decimal conversion, along with the method of conversion are given below:

Example 1: Binary to decimal conversion: 1101

1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 
= 8 + 4 + 0 + 1 
= 13

Example 2: Binary to decimal conversion: 101010

1 × 25 + 0 × 24 + 1 × 23 + 0 × 22 + 1 × 21 + 0 × 20 
= 32 + 0 + 8 + 0 + 2 + 0 
= 42

Example 3: Binary to decimal conversion: 1111

1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 
= 8 + 4 + 2 + 1 
= 15

Example 4:Binary to decimal conversion: 1001100

1 × 26 + 0 × 25 + 0 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20 
= 64 + 0 + 0 + 8 + 4 + 0 + 0 
= 76

Example 5: Binary to decimal conversion: 11001

1 × 24 + 1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 
= 16 + 8 + 0 + 0 + 1 
= 25

Example 6:Binary to decimal conversion: 111000

1 × 25 + 1 × 24 + 1 × 23 + 0 × 22 + 0 × 21 + 0 × 20 
= 32 + 16 + 8 + 0 + 0 + 0 
= 56

Example 7: Binary to decimal conversion: 101

1 × 22 + 0 × 21 + 1 × 20 
= 4 + 0 + 1 
= 5

Example 8: Binary to decimal conversion: 11010

1 × 24 + 1 × 23 + 0 × 22 + 1 × 21 + 0 × 20 
= 16 + 8 + 0 + 2 + 0 
= 26

Example 9: Binary to decimal conversion: 1001

1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 
= 8 + 0 + 0 + 1 
= 9

Example 10: Binary to decimal conversion: 1110001

1 × 26 + 1 × 25 + 1 × 24 + 0 × 23 + 0 × 22 + 0 × 21 + 1 × 20 
= 64 + 32 + 16 + 0 + 0 + 0 + 1 
= 113

Conversion of fractional binary numbers to decimal numbers

Converting binary fractions to decimal fractions involves a similar process to converting whole numbers. Each binary digit (bit) in the fractional part represents a decreasing power of 2, just like in the whole number part where each bit represents an increasing power of 2, i.e., the process is about breaking down the binary fractional part into its component bits and multiplying each bit by the appropriate power of 2 to get the corresponding decimal value.

Few examples of converting binary fractional values to decimal fractional values, along with the method of conversion are given below:

Example 1: Convert 0.1011 binary to decimal

0.1011 binary = 1 × 2−1 + 0 × 2−2 + 1 × 2−3 + 1 × 2−4
             = 0.5 + 0 + 0.125 + 0.0625
             = 0.6875 decimal

Example 2: Convert 0.11001 binary to decimal

0.11001 binary = 1 × 2−1 + 1 × 2−2 + 0 × 2−3 + 0 × 2−4 + 1 × 2−5
              = 0.5 + 0.25 + 0 + 0 + 0.03125
              = 0.78125 decimal

Example 3: Convert 0.011001 binary to decimal

0.011001 binary = 0 × 2−1 + 1 × 2−2 + 1 × 2−3 + 0 × 2−4 + 0 × 2−5 + 1 × 2−6
              = 0 + 0.25 + 0.125 + 0 + 0 + 0.015625
              = 0.390625 decimal

Example 4: Convert 0.101010 binary to decimal

0.101010 binary = 1 × 2−1 + 0 × 2−2 + 1 × 2−3 + 0 × 2−4 + 1 × 2−5 + 0 × 2−6
              = 0.5 + 0 + 0.125 + 0 + 0.03125 + 0
              = 0.65625 decimal

Example 5: Convert 0.001 binary to decimal

0.001 binary = 0 × 2−1 + 0 × 2−2 + 1 × 2−3
           = 0 + 0 + 0.125
           = 0.125 decimal

Example 6: Convert 0.1101101 binary to decimal

0.1101101 binary = 1 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + 1 × 2−5 + 0 × 2−6 + 1 × 2−7
               = 0.5 + 0.25 + 0 + 0.0625 + 0.03125 + 0 + 0.0078125
               = 0.8515625 decimal

Example 7: Convert 0.010101 binary to decimal

0.010101 binary = 0 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + 0 × 2−5 + 1 × 2−6
             = 0 + 0.25 + 0 + 0.0625 + 0 + 0.015625
             = 0.328125 decimal

Example 8: Convert 0.111 binary to decimal

0.111 binary = 1 × 2−1 + 1 × 2−2 + 1 × 2−3
           = 0.5 + 0.25 + 0.125
           = 0.875 decimal

Example 9: Convert 0.00011 binary to decimal

0.00011 binary = 0 × 2−1 + 0 × 2−2 + 0 × 2−3 + 1 × 2−4 + 1 × 2−5
             = 0 + 0 + 0 + 0.0625 + 0.03125
             = 0.09375 decimal

Example 10: Convert 0.10011001 binary to decimal

0.10011001 binary = 1 × 2−1 + 0 × 2−2 + 0 × 2−3 + 1 × 2−4 + 1 × 2−5 + 0 × 2−6 + 0 × 2−7 + 1 × 2−8
                = 0.5 + 0 + 0 + 0.0625 + 0.03125 + 0 + 0 + 0 + 0.00390625
                = 0.59765625 decimal

Converting a binary number to octal number

Converting a binary number to octal involves grouping the binary digits in sets of three and then converting each group to its octal equivalent. The binary digits in sets of three from right to left are grouped, and if the leftmost group has fewer than three digits, add leading zeros to make it a complete group. Then, convert each group to its octal equivalent to obtain the final octal representation. Few examples of binary to octal conversions along with the steps for each conversion are given below:

Example 1: Convert 1101011 from binary to octal

Step 1: Group the binary digits in sets of three, adding leading zeros if necessary: 001 101 011
Step 2: Convert each group to its octal equivalent: 1 5 3
Result: 1101011 (binary) = 153 (octal)

Example 2: Convert 1010110 from binary to octal

Step 1: Group the binary digits in sets of three: 001 010 110
Step 2: Convert each group to octal: 1 2 6
Result: 1010110 (binary) = 126 (octal)

Example 3: Convert 11001010 from binary to octal

Step 1: Group the binary digits in sets of three: 001 100 101 0
Step 2: Convert each group to octal: 1 4 5 0
Result: 11001010 (binary) = 1450 (octal)

Example 4: Convert 101110111 from binary to octal

Step 1: Group the binary digits in sets of three: 001 011 101 110
Step 2: Convert each group to octal: 1 3 5 6
Result: 101110111 (binary) = 1356 (octal)

Example 5: Convert 11110000 from binary to octal

Step 1: Group the binary digits in sets of three: 001 111 000
Step 2: Convert each group to octal: 1 7 0
Result: 11110000 (binary) = 170 (octal)

Example 6: Convert 1101101101 from binary to octal

Step 1: Group the binary digits in sets of three: 001 101 101 101
Step 2: Convert each group to octal: 1 5 5 5
Result: 1101101101 (binary) = 1555 (octal)

Example 7: Convert 100111010 from binary to octal

Step 1: Group the binary digits in sets of three: 100 111 010
Step 2: Convert each group to octal: 4 7 2
Result: 100111010 (binary) = 472 (octal)

Example 8: Convert 101010101010 from binary to octal

Step 1: Group the binary digits in sets of three: 001 010 101 010 101 0
Step 2: Convert each group to octal: 1 2 5 2 5 0
Result: 101010101010 (binary) = 125250 (octal)

Example 9: Convert 110011001101 from binary to octal

Step 1: Group the binary digits in sets of three: 001 100 110 011 010
Step 2: Convert each group to octal: 1 4 6 3 2
Result: 110011001101 (binary) = 14632 (octal)

Example 10: Convert 111111111111 from binary to octal

Step 1: Group the binary digits in sets of three: 111 111 111 111
Step 2: Convert each group to octal: 7 7 7 7
Result: 111111111111 (binary) = 7777 (octal)

Conversion of binary numbers to hexadecimal number

Binary numbers are base-2 numbers, while hexadecimal numbers are base-16 numbers. In binary, each digit represents a power of 2, and in hexadecimal, each digit represents a power of 16. To convert from binary to hexadecimal, you can follow these steps:

  1. Group the binary digits in sets of 4, starting from the right.
  2. If the leftmost group has less than 4 digits, add leading zeros.
  3. Convert each group to its hexadecimal equivalent.
  4. Combine the hexadecimal groups to get the final hexadecimal representation.

Few examples binary numbers to hexadecimal along with the method of conversion are given below:

Example 1:

Binary: 101101
Step 1:   10 | 1101
Step 2: 0010 | 1101
Step 3:    2 |    D
Hexadecimal: 2D

Example 2:

Binary: 110110111
Step 1:    1 | 1011 | 0111
Step 2: 0001 | 1011 | 0111
Step 3:    1 |    B |    7
Hexadecimal: 1B7

Example 3:

Binary: 10010101
Step 1: 1010 | 0101
Step 2: 1010 | 0101
Step 3:   A  |    5
Hexadecimal: A5

Example 4:

Binary: 110010101110
Step 1: 1100 | 1010 | 1110
Step 2: 1100 | 1010 | 1110
Step 3:    C |    A |    E
Hexadecimal: CAE

Example 5:

Binary: 1010101010101010
Step 1: 1010 | 1010 | 1010 | 1010
Step 3:    A |    A |    A |    A
Hexadecimal: AAAA

Example 6:

Binary: 1111110000001111
Step 1: 1111 | 1100 | 0000 | 1111
Step 3:  F   |    C |    0 |    F
Hexadecimal: FC0F

Example 7:

Binary: 1010011101
Step 1:   10 | 1001 | 1101
Step 2: 0010 | 1001 | 1101 
Step 3:    2 |    9 |    D    
Hexadecimal: 29D

Example 8:

Binary: 110111101010101
Step 1:  110 | 1111 | 0101 | 0101
Step 2: 0110 | 1111 | 0101 | 0101
Step 3:    6 |    F |    5 |    5
Hexadecimal: 6F55

Example 9:

Binary: 111000111
Step 1:    1 | 1100 | 0111
Step 2: 0001 | 1100 | 0111
Step 3:    1 |    C |    7
Hexadecimal: 1C7

Example 10:

Binary: 10011001100100
Step 1:   10 | 0110 | 0110 | 0100
Step 2: 0010 | 0110 | 0110 | 0100
Step 3:    2 |    6 |    6 |    4
Hexadecimal: 2664

Decimal to binary conversion

Binary is a base-2 numbering system, meaning it uses only two symbols: 0 and 1. To convert a decimal number to binary, you can use the process of repeated division by 2. Few examples of decimal to binary conversions along with the step-by-step method of conversion are given below:

Example 1: Convert 10 to binary

1. Divide 10 by 2: Quotient = 5, Remainder = 0.
2. Divide  5 by 2: Quotient = 2, Remainder = 1.
3. Divide  2 by 2: Quotient = 1, Remainder = 0.
4. Divide  1 by 2: Quotient = 0, Remainder = 1.

Reading the remainders in reverse order: 1010. So, decimal 10 is equal to binary 1010.

Example 2: Convert 25 to binary

1. Divide 25 by 2: Quotient = 12, Remainder = 1.
2. Divide 12 by 2: Quotient =  6, Remainder = 0.
3. Divide  6 by 2: Quotient =  3, Remainder = 0.
4. Divide  3 by 2: Quotient =  1, Remainder = 1.
5. Divide  1 by 2: Quotient =  0, Remainder = 1.

Reading the remainders in reverse order: 11001. So, decimal 25 is equal to binary 11001.

Example 3: Convert 42 to binary

1. Divide 42 by 2: Quotient = 21, Remainder = 0.
2. Divide 21 by 2: Quotient = 10, Remainder = 1.
3. Divide 10 by 2: Quotient =  5, Remainder = 0.
4. Divide  5 by 2: Quotient =  2, Remainder = 1.
5. Divide  2 by 2: Quotient =  1, Remainder = 0.
6. Divide  1 by 2: Quotient =  0, Remainder = 1.

Reading the remainders in reverse order: 101010. So, decimal 42 is equal to binary 101010.

Example 4: Convert 128 to binary

1. Divide 128 by 2: Quotient = 64, Remainder = 0.
2. Divide  64 by 2: Quotient = 32, Remainder = 0.
3. Divide  32 by 2: Quotient = 16, Remainder = 0.
4. Divide  16 by 2: Quotient =  8, Remainder = 0.
5. Divide   8 by 2: Quotient =  4, Remainder = 0.
6. Divide   4 by 2: Quotient =  2, Remainder = 0.
7. Divide   2 by 2: Quotient =  1, Remainder = 0.
8. Divide   1 by 2: Quotient =  0, Remainder = 1.

Reading the remainders in reverse order: 10000000. So, decimal 128 is equal to binary 10000000.

Example 5: Convert 63 to binary

1. Divide 63 by 2: Quotient = 31, Remainder = 1.
2. Divide 31 by 2: Quotient = 15, Remainder = 1.
3. Divide 15 by 2: Quotient =  7, Remainder = 1.
4. Divide  7 by 2: Quotient =  3, Remainder = 1.
5. Divide  3 by 2: Quotient =  1, Remainder = 1.
6. Divide  1 by 2: Quotient =  0, Remainder = 1.

Reading the remainders in reverse order: 111111. So, decimal 63 is equal to binary 111111.

Example 6: Convert 77 to binary

1. Divide 77 by 2: Quotient = 38, Remainder = 1.
2. Divide 38 by 2: Quotient = 19, Remainder = 0.
3. Divide 19 by 2: Quotient =  9, Remainder = 1.
4. Divide  9 by 2: Quotient =  4, Remainder = 1.
5. Divide  4 by 2: Quotient =  2, Remainder = 0.
6. Divide  2 by 2: Quotient =  1, Remainder = 0.
7. Divide  1 by 2: Quotient =  0, Remainder = 1.

Reading the remainders in reverse order: 1001101. So, decimal 77 is equal to binary 1001101.

Example 7: Convert 200 to binary

1. Divide 200 by 2: Quotient = 100, Remainder = 0.
2. Divide 100 by 2: Quotient =  50, Remainder = 0.
3. Divide  50 by 2: Quotient =  25, Remainder = 1.
4. Divide  25 by 2: Quotient =  12, Remainder = 1.
5. Divide  12 by 2: Quotient =   6, Remainder = 0.
6. Divide   6 by 2: Quotient =   3, Remainder = 0.
7. Divide   3 by 2: Quotient =   1, Remainder = 1.
8. Divide   1 by 2: Quotient =   0, Remainder = 1.

Reading the remainders in reverse order: 11001000. So, decimal 200 is equal to binary 11001000.

Example 8: Convert 500 to binary

1. Divide 500 by 2: Quotient = 250, Remainder = 0.
2. Divide 250 by 2: Quotient = 125, Remainder = 0.
3. Divide 125 by 2: Quotient =  62, Remainder = 1.
4. Divide  62 by 2: Quotient =  31, Remainder = 1.
5. Divide  31 by 2: Quotient =  15, Remainder = 1.
6. Divide  15 by 2: Quotient =   7, Remainder = 1.
7. Divide   7 by 2: Quotient =   3, Remainder = 1.
8. Divide   3 by 2: Quotient =   1, Remainder = 1.
9. Divide   1 by 2: Quotient =   0, Remainder = 1.

Reading the remainders in reverse order: 111110100. So, decimal 500 is equal to binary 111

Conversion of decimal fractions to binary number

Converting decimal fractions to binary involves a process similar to converting whole numbers but applied to the fractional part. Some decimal fractions might not have an exact binary representation and may result in repeating patterns or rounding.

Method of decimal fraction to binary number:

  1. Multiply the fractional part by 2.
  2. The whole number part of the result becomes the next binary digit.
  3. Repeat the process with the fractional part of the result.
  4. Continue until the fractional part becomes zero or until you have the desired number of binary digits. Few examples of converting decimal fractions to binary, along with the method of conversion are given below:

Example 1: Convert 0.25 to binary.

0.25 × 2 = 0.5 ⇒ Binary: 0.0
0.5  × 2 = 1.0 ⇒ Binary: 0.01

So, 0.25 in binary is 0.01.

Example 2: Convert 0.625 to binary.

0.625 × 2 = 1.25 ⇒ Binary: 0.1
0.25  × 2 = 0.5  ⇒ Binary: 0.10

So, 0.625 in binary is 0.101.

Example 3: Convert 0.125 to binary.

0.125 × 2 = 0.25 ⇒ Binary: 0.0
0.25  × 2 = 0.5  ⇒ Binary: 0.00
0.5   × 2 = 1.0  ⇒ Binary: 0.001

So, 0.125 in binary is 0.001.

Example 4: Convert 0.3 to binary.

0.3 × 2 = 0.6 ⇒ Binary: 0.0
0.6 × 2 = 1.2 ⇒ Binary: 0.01
0.2 × 2 = 0.4 ⇒ Binary: 0.010

So, 0.3 in binary is approximately 0.0101 (rounded due to repeating pattern).

Example 5: Convert 0.875 to binary.

0.875 × 2 = 1.75 ⇒ Binary: 0.1
0.75  × 2 = 1.5  ⇒ Binary: 0.11
0.5   × 2 = 1.0  ⇒ Binary: 0.111

So, 0.875 in binary is 0.111.

Example 6: Convert 0.0625 to binary.

0.0625 × 2 = 0.125 ⇒ Binary: 0.0
0.125  × 2 = 0.25  ⇒ Binary: 0.00
0.25   × 2 = 0.5   ⇒ Binary: 0.000
0.5    × 2 = 1.0   ⇒ Binary: 0.0000

So, 0.0625 in binary is 0.0000.

Example 7: Convert 0.7 to binary.

0.7 × 2 = 1.4 ⇒ Binary: 0.1
0.4 × 2 = 0.8 ⇒ Binary: 0.10
0.8 × 2 = 1.6 ⇒ Binary: 0.101
0.6 × 2 = 1.2 ⇒ Binary: 0.1011

So, 0.7 in binary is approximately 0.1011 (rounded due to repeating pattern).

Example 8: Convert 0.15625 to binary.

0.15625 × 2 = 0.3125 ⇒ Binary: 0.0
0.3125  × 2 = 0.625  ⇒ Binary: 0.00
0.625   × 2 = 1.25   ⇒ Binary: 0.001
0.25    × 2 = 0.5    ⇒ Binary: 0.0010

So, 0.15625 in binary is 0.0010.

Example 9: Convert 0.2 to binary.

0.2 × 2 = 0.4 ⇒ Binary: 0.0
0.4 × 2 = 0.8 ⇒ Binary: 0.00
0.8 × 2 = 1.6 ⇒ Binary: 0.001
0.6 × 2 = 1.2 ⇒ Binary: 0.0011

So, 0.2 in binary is approximately 0.0011 (rounded due to repeating pattern).

Example 10: Convert 0.9 to binary.

0.9 × 2 = 1.8 ⇒ Binary: 0.1
0.8 × 2 = 1.6 ⇒ Binary: 0.11

So, 0.9 in binary is approximately 0.11 (rounded due to repeating pattern).

Decimal to octal number conversion (Error in example)

Octal is a base-8 number system, which means it uses digits 0 through 7. To convert a decimal number to octal, you can follow these steps:

  1. Divide the decimal number by 8.
  2. Note down the remainder.
  3. Continue dividing the quotient from the previous step by 8 and noting down the remainders until the quotient becomes 0.
  4. The octal number is formed by writing the remainders in reverse order, i.e., reverse the remainders obtained from the division steps to get the correct octal representation of the decimal number.

Few examples of decimal to octal conversions are given below:

Example 1:

Decimal: 13
Division steps:
13 ÷ 8 = 1 remainder 5
Octal: 15

Example 2:

Decimal: 42
Division steps:
42 ÷ 8 = 5 remainder 2
 5 ÷ 8 = 0 remainder 5
Octal: 52

Example 3:

Decimal: 89
Division steps:
89 ÷ 8 = 11 remainder 1
11 ÷ 8 = 1  remainder 3
 1 ÷ 8 = 0  remainder 1
Octal: 131

Example 4:

Decimal: 255
Division steps:
255 ÷ 8 = 31 remainder 7
 31 ÷ 8 = 3  remainder 7
  3 ÷ 8 = 0  remainder 3
Octal: 377

Example 5:

Decimal: 512
Division steps:
512 ÷ 8 = 64 remainder 0
    ÷ 8 =    remainder 4
    ÷ 8 =    remainder 6
Octal: 640

Example 6:

Decimal: 1024
Division steps:
1024 ÷ 8 = 128 remainder 0
     ÷ 8 =     remainder 0 
     ÷ 8 =     remainder 0
     ÷ 8 =     remainder 1	 
Octal: 1000

Example 7:

Decimal: 4096
Division steps:
4096 ÷ 8 = 512 remainder 0
     ÷ 8 =     remainder 0 
     ÷ 8 =     remainder 0
     ÷ 8 =     remainder 5	 
Octal: 5000

Example 8:

Decimal: 10000
Division steps:
10000 ÷ 8 = 1250 remainder 0
      ÷ 8 =      remainder 5
      ÷ 8 =      remainder 4
      ÷ 8 =      remainder 4
      ÷ 8 =      remainder 1	  
Octal: 14450

Example 9:

Decimal: 78901
Division steps:
78901 ÷ 8 = 9862 remainder 6
9862  ÷ 8 = 1232 remainder 0
1232  ÷ 8 =  154 remainder 5
      ÷ 8 =      remainder 6
      ÷ 8 =      remainder 3
      ÷ 8 =      remainder 2	  
Octal: 236506

Example 10:

Decimal: 65536
Division steps:
65536 ÷ 8 = 8192 remainder 0
Octal: 20000

Decimal fractions to octal number conversion (Error in example)

Converting decimal fractions to octal involves converting the fractional part of the decimal number to its octal equivalent.

Method of Conversion:

  1. Multiply the decimal fraction by 8 (the base of octal).
  2. Record the integer part of the result as the next digit in the octal representation.
  3. Take the fractional part of the result and repeat step 1.
  4. Continue this process until the fractional part becomes zero or until you have obtained the desired number of octal digits.

The factional decimal to octal conversion process might result in a finite number of octal digits or a repeating pattern, depending on the decimal fraction being converted.

Few examples using the method of conversion are given below:

Example 1:

Decimal Fraction: 0.125

1. 0.125 × 8 = 1.0
2. Octal Digit: 1
3. Fractional Part: 0
Octal Equivalent: 0.125 (decimal) = 0.1 (octal)

Example 2:

Decimal Fraction: 0.625

1. 0.625 × 8 = 5.0
2. Octal Digit: 5
3. Fractional Part: 0
Octal Equivalent: 0.625 (decimal) = 0.5 (octal)

Example 3:

Decimal Fraction: 0.3

1. 0.3 × 8 = 2.4
2. Octal Digit: 2
3. Fractional Part: 0.4
4. 0.4 × 8 = 3.2
5. Octal Digit: 3
6. Fractional Part: 0.2
Octal Equivalent: 0.3 (decimal) = 0.23 (octal)

Example 4:

Decimal Fraction: 0.8

1. 0.8 × 8 = 6.4
2. Octal Digit: 6
3. Fractional Part: 0.4
4. 0.4 × 8 = 3.2
5. Octal Digit: 3
6. Fractional Part: 0.2
Octal Equivalent: 0.8 (decimal) = 0.63 (octal)

Example 5:

Decimal Fraction: 0.0125

1. 0.0125 × 8 = 0.1
2. Octal Digit: 0
3. Fractional Part: 0.1
Octal Equivalent: 0.0125 (decimal) = 0.1 (octal)

Example 6:

Decimal Fraction: 0.4

1. 0.4 × 8 = 3.2
2. Octal Digit: 3
3. Fractional Part: 0.2
Octal Equivalent: 0.4 (decimal) = 0.32 (octal)

Example 7:

Decimal Fraction: 0.875

1. 0.875 × 8 = 7.0
2. Octal Digit: 7
3. Fractional Part: 0
Octal Equivalent: 0.875 (decimal) = 0.7 (octal)

Example 8:

Decimal Fraction: 0.6

1. 0.6 × 8 = 4.8
2. Octal Digit: 4
3. Fractional Part: 0.8
4. 0.8 × 8 = 6.4
5. Octal Digit: 6
6. Fractional Part: 0.4
Octal Equivalent: 0.6 (decimal) = 0.46 (octal)

Example 9:

Decimal Fraction: 0.025

1. 0.025 × 8 = 0.2
2. Octal Digit: 0
3. Fractional Part: 0.2
Octal Equivalent: 0.025 (decimal) = 0.2 (octal)

Example 10:

Decimal Fraction: 0.0375

1. 0.0375 × 8 = 0.3
2. Octal Digit: 0
3. Fractional Part: 0.3
Octal Equivalent: 0.0375 (decimal) = 0.3 (octal)

Decimal to hexadecimal conversion (Error in example)

Decimal to hexadecimal conversion involves dividing the decimal number by 16 repeatedly and noting down the remainders at each step. Then, the remainders are converted into their hexadecimal equivalents. The numbers from 10 to 15 are represented as A to F, respectively, in hexadecimal number system.

Few examples with the step-by-step process for each example are given below:

Example 1: Convert 23 in decimal to hexadecimal:

1. Divide 23 by 16: Quotient = 1, Remainder = 7 (23 = 1 × 16 + 7)
2. The remainder 7 in decimal is equivalent to 7 in hexadecimal.
3. Therefore, the hexadecimal representation of 23 is 17.

Example 2: Convert 104 in decimal to hexadecimal:

1. Divide 104 by 16: Quotient = 6, Remainder = 8 (104 = 6 × 16 + 8)
2. The remainder 8 in decimal is equivalent to 8 in hexadecimal.
3. Therefore, the hexadecimal representation of 104 is 68.

Example 3: Convert 255 in decimal to hexadecimal:

1. Divide 255 by 16: Quotient = 15, Remainder = 15 (255 = 15 × 16 + 15)
2. The remainder 15 in decimal is equivalent to F in hexadecimal.
3. Therefore, the hexadecimal representation of 255 is FF.

Example 4: Convert 512 in decimal to hexadecimal:

1. Divide 512 by 16: Quotient = 32, Remainder = 0 (512 = 32 × 16 + 0)
2. The remainder 0 in decimal is equivalent to 0 in hexadecimal.
3. Therefore, the hexadecimal representation of 512 is 200.

Example 5: Convert 789 in decimal to hexadecimal:

1. Divide 789 by 16: Quotient = 49, Remainder = 5 (789 = 49 × 16 + 5)
2. The remainder 5 in decimal is equivalent to 5 in hexadecimal.
3. Therefore, the hexadecimal representation of 789 is 315.

Example 6: Convert 1024 in decimal to hexadecimal:

1. Divide 1024 by 16: Quotient = 64, Remainder = 0 (1024 = 64 × 16 + 0)
2. The remainder 0 in decimal is equivalent to 0 in hexadecimal.
3. Therefore, the hexadecimal representation of 1024 is 400.

Example 7: Convert 4096 in decimal to hexadecimal:

1. Divide 4096 by 16: Quotient = 256, Remainder = 0 (4096 = 256 × 16 + 0)
2. The remainder 0 in decimal is equivalent to 0 in hexadecimal.
3. Therefore, the hexadecimal representation of 4096 is 1000.

Example 8: Convert 1500 in decimal to hexadecimal:

1. Divide 1500 by 16: Quotient = 93, Remainder = 12 (1500 = 93 × 16 + 12)
2. The remainder 12 in decimal is equivalent to C in hexadecimal.
3. Therefore, the hexadecimal representation of 1500 is 5DC.

Example 9: Convert 7689 in decimal to hexadecimal:

1. Divide 7689 by 16: Quotient = 480, Remainder = 9 (7689 = 480 × 16 + 9)
2. The remainder 9 in decimal is equivalent to 9 in hexadecimal.
3. Therefore, the hexadecimal representation of 7689 is 1E09.

Example 10: Convert 65535 in decimal to hexadecimal:

1. Divide 65535 by 16: Quotient = 4095, Remainder = 15 (65535 = 4095 × 16 + 15)
2. The remainder 15 in decimal is equivalent to F in hexadecimal.
3. Therefore, the hexadecimal representation of 65535 is FFFF.