To examine underlying physical concepts of applications of mechanics, we’ll look carefully at three kinds of everyday activities and objects: (1) skating, (2) falling balls, and (3) ramps. In Skating, we see how objects move when nothing pushes on them. In Falling Balls, we find out how that movement can be influenced by gravity. In Ramps, we explore mechanical advantage and how gradual inclines make it possible to lift heavy objects without pushing very hard.
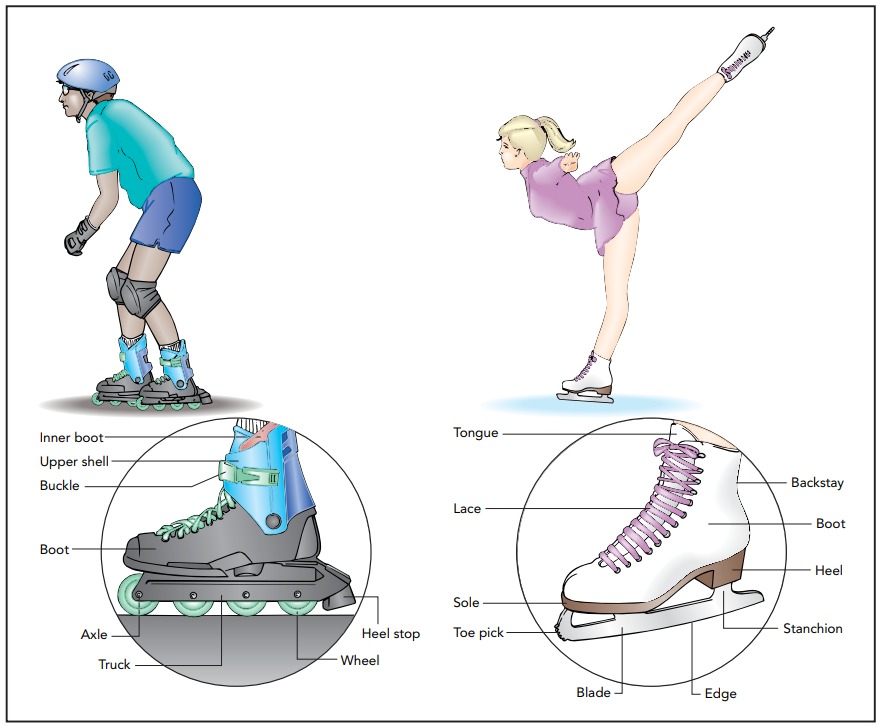
Skating - Inertia
Like many sports, skating is trickier than it appears. If you’re a first-time skater, you’re likely to find yourself getting up repeatedly from the ground or ice, and it will take some practice before you can glide smoothly forward or come gracefully to a stop. But whether you’re wearing ice skates or roller skates, the physics of your motion is surprisingly simple. When you’re on a level surface with your skates pointing forward, you coast!
The correct answer to that apparently simple question eluded people for thousands of years; even Aristotle, perhaps the most learned philosopher of the classical world, was mistaken about it and it took the remarkable Italian astronomer, mathematician, and physicist Galileo Galilei many years of careful observation and logical analysis to answer that question. The solution he came up with, like the question itself, is simple: if the person is stationary, she will remain stationary; if she is moving in some particular direction, she will continue moving in that direction at a steady pace, following a straight-line path. This property of steady motion in the absence of any outside influence is called inertia.
A body in motion tends to remain in motion; a body at rest tends to remain at rest.
The main reason that Aristotle failed to discover inertia, and why we often overlook inertia ourselves, is friction. When you slide across the floor in your shoes, friction quickly slows you to a stop and masks your inertia. To make inertia more obvious, we must get rid of friction. That’s why you’re wearing skates. Skates almost completely eliminate friction, at least in one direction, so that you can glide effortlessly across the ice or roller rink and experience your own inertia.
The five important physical quantities relating to motion and look at their relationships to one another. These quantities are position, velocity, mass, acceleration, and force. When you’re gliding freely, however, with nothing pushing you horizontally, your velocity is particularly easy to describe. Since you travel at a steady speed along a straightline path, your velocity is constant—it never changes. In a word, you coast. And if you happen to be at rest with nothing pushing you horizontally, you remain at rest. Your velocity is constantly zero.
The description of inertia in terms of velocity: an object that is not subject to any outside influences moves at a constant velocity, covering equal distances in equal times along a straight-line path. The outside influences referred to in this law are called forces, a technical term for pushes and pulls. This statement is frequently identified as Newton’s first law of motion, after its discoverer, the English mathematician and physicist Sir Isaac Newton. An object that moves in accordance with Newton’s first law is said to be inertial.
NEWTON’S FIRST LAW OF MOTION: An object that is not subject to any outside forces moves at a constant velocity, covering equal distances in equal times along a straight-line path.
Why does a moving hockey puck continue to slide across an ice rink even though no one is pushing on it?
As you glide forward with nothing pushing you horizontally, what prevents your speed and direction from changing? The answer is your mass. Mass is the measure of your inertia, your resistance to changes in velocity. Almost everything in the universe has mass. Mass has no direction. Because you have mass, your velocity will change only if something pushes on you—that is, only if you experience a force. You’ll keep moving steadily in a straight path until something exerts a force on you to stop you or send you in another direction.
When something pushes on you, your velocity changes; in other words, you accelerate. Acceleration, our fourth vector quantity, measures the rate at which your velocity is changing with time. Any change in your velocity is acceleration, whether you’re speeding up, slowing down, or turning. If either your speed or direction of travel is changing, you’re accelerating!
Acceleration has a magnitude and a direction. To see how these two parts of acceleration work, imagine that you’re at the starting line of a speedskating race, waiting for it to begin. The starting buzzer sounds, and you’re off! You dig your skates into the surface beneath you and begin to accelerate—your speed increases and you cover ground more and more quickly. The magnitude of your acceleration depends on how hard the skating surface pushes you forward. If it’s a long race and you’re not in a hurry, you take your time getting up to full speed. The surface pushes you forward gently and the magnitude of your acceleration is small. Your velocity changes slowly. However, if the race is a sprint and you need to reach top speed as quickly as possible, you spring forward hard and the surface exerts an enormous forward force on you. The magnitude of your acceleration is large, and your velocity changes rapidly. In this case, you can actually feel your inertia opposing your efforts to pick up speed. Even when you’re not trying to speed up or slow down, you can still accelerate. As you steer your skates or go over a bump, you experience sideways or up–down forces that change your direction of travel and thus cause you to accelerate.
Finally the race is over, and you skid to a stop. You’re accelerating again, but this time in the backward direction—opposite your forward velocity. Although we often call this process deceleration, it’s just a special type of acceleration. Your forward velocity gradually diminishes until you come to rest.
Your acceleration depends on the strength of that net force: the stronger the net force, the more you accelerate. However, your acceleration also depends on your mass: the more massive you are, the less you accelerate. Your acceleration is equal to the net force exerted on you divided by your mass.
The net force exerted on an object is equal to that object’s mass times its acceleration.
So far we’ve explored five principles:
1. Your position indicates exactly where you’re located.
2. Your velocity measures the rate at which your position is changing with time.
3. Your acceleration measures the rate at which your velocity is changing with time.
4. To accelerate, you must experience a net force.
5. The greater your mass, the less acceleration you experience for a given net force.
It’s much easier to stop a bicycle traveling toward you at 5 kilometers per hour than an automobile traveling toward you at the same velocity. What accounts for this difference?
While skating alone is peaceful, it’s usually more fun with other skaters around. That way, you have people to talk to and an audience for your athleticism and artistry. However, with several skaters coasting on the ice at once, there’s a question of perspective. As you glide steadily past a friend, the two of you see the world somewhat differently. From your perspective, you are motionless and your friend is moving. From your
friend’s perspective, though, your friend is motionless and you are moving. Who is right?
It turns out that you’re both right and that physics has a way of accommodating this apparent paradox. Each of you is observing the world from a different inertial frame of reference, the viewpoint of an inertial object—an object that is not accelerating and that moves according to Newton’s first law.
Skating - Inertia
Falling Objects - Inertia
We’ve all dropped balls from our hands or seen them arc gracefully through the air after being thrown. These motions are simplicity itself and, not surprisingly, they’re governed by only a few universal rules.
A ball has a weight. Evidently it’s a force, since both the newton (N). To understand what weight is, however—and, in particular, where it comes from—we need to look at gravity. Gravity is a physical phenomenon that produces attractive forces between every pair of objects in the universe. In our daily lives, however, the only object massive enough and near enough to have obvious gravitational effects on us is our planet, Earth. Gravity weakens with distance; the moon and sun are so far away that we notice their gravities only through such subtle effects as the ocean tides.
Earth’s gravity exerts a downward force on any object near its surface. That object is attracted directly toward the center of Earth with a force we call the object’s weight. weight is how hard gravity pulls on a ball, and mass is how difficult that ball is to accelerate. You can lose weight either by reducing your mass or by going someplace, like a small planet, where the gravity is weaker.
Out in deep space, far from any celestial object that exerts significant gravity, would an astronaut weigh anything? Would that astronaut have a mass?
A falling ball is one that has only its weight, the force due to gravity, acting on it. A stone dropped from rest descends faster with each passing second, but you can give it a boost by throwing it downward instead of just letting go.
The longer a stone has been falling, the more its height diminishes with each passing second. However, it won’t overtake a stone that was dropped next to it at an earlier time or dropped from beneath it at the same time.
What happens if you don’t toss the ball exactly straight up? Suppose you throw the ball upward at some angle. When you drop the ball from rest or toss it straight up, its motion is entirely vertical and only the upward components of its position, velocity, and acceleration are important. The ball thrown forward arcs forward with a position specified at each moment by its altitude (its upward component) and its distance downfield (its forward component).

Once you’ve thrown the ball forward and are no longer touching it, its motion can be broken into two parts: its upward motion and its forward motion. Part of the ball’s initial velocity is in the upward direction, and that upward component of velocity determines the object’s ascent and descent. Part of the ball’s initial velocity is in the forward direction, and that forward component of velocity determines the ball’s progress downfield.
Because the ball is accelerating straight downward, the forward component of its acceleration is zero and the forward component of its velocity thus remains constant. The ball travels downfield at a steady rate throughout its flight. Overall, the upward component of the ball’s initial velocity determines how high the ball goes and how long it stays aloft before striking the ground, while the forward component of the initial velocity determines how quickly the ball travels downfield during its time aloft.
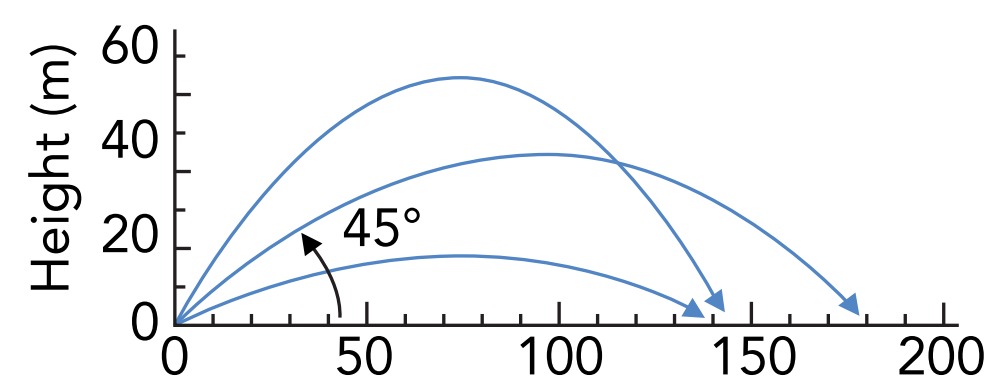
Just before the ball hits the ground it still has its original forward component of velocity, but its upward component of velocity is now negative—the ball is moving downward. The total velocity of the ball is composed of these two components. The ball starts with its velocity directed up and forward, and finishes with its velocity directed down and forward. If you want a ball or shot put to hit the ground as far from your feet as possible, you should keep it aloft for a long time and give it a sizable forward component of velocity; in other words, you must achieve a good balance between the upward and forward components of velocity
Falling Objects - Inertia
Ramps - Mechanical Advantage
Imagine, for example, an object resting on the floor. That object experiences both its downward weight and an upward force from the floor. If the floor is level, the object doesn’t accelerate; but if the floor is tilted, so that it forms a ramp, the object accelerates downhill.
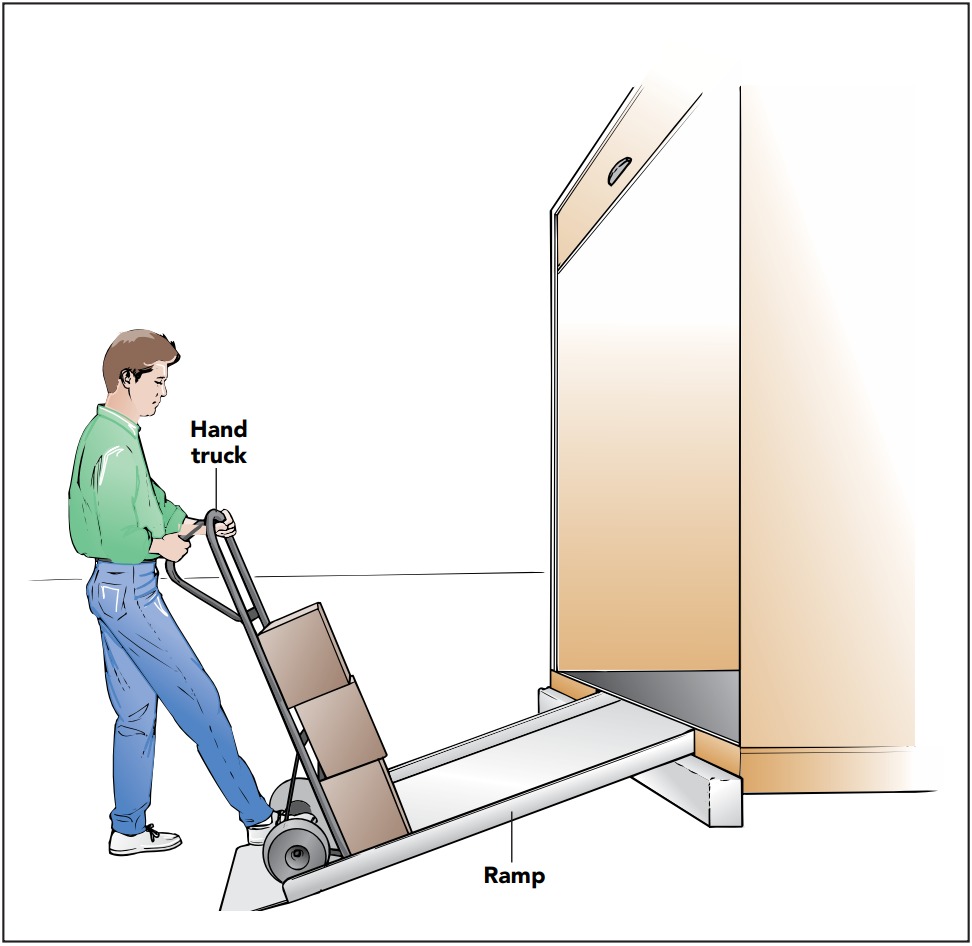
Throughout the ages, ramps, also known as inclined planes, have made tasks to move heavy object uphill possible. Because ramps can exert the enormous upward forces needed to lift stone and steel, they’ve been essential building equipment since the days of the pyramids.
If you push on any object, that object will push back on you with an equal amount of force in exactly the opposite direction. This rule—often expressed as “for every action, there is an equal but opposite reaction”—is known as Newton’s third law of motion, the last of his three laws. The universality of this law is astounding. Whether an object is large or small, hard or soft, stationary or faster than a rocket, if you can push on it, it will push back on you with an equal but oppositely directed force.


To do work on an object, you must push on it while it moves in the direction of your push. The work you do on it is the force you exert on it times the distance it travels along the direction of your force. If you’re not pushing or it’s not moving, then you’re not working. The capacity to make things happen is called energy. The relationship between energy and work is analogous to the relationship between money and spending: money is what is transferred, and spending does the transferring. Sensible, law-abiding citizens don’t create or destroy money; instead, they transfer it among themselves through spending. Just as the most interesting aspect of money is spending it, so the most interesting aspect of energy is doing work with it. We can define money as the capacity to spend, just as we define energy as the capacity to do work.
Unfortunately, you probably can’t carry a grand piano up a ladder by yourself. You need a ramp, both to help you support the piano and to make it easier for you to raise the piano to the second floor. Like the sidewalk, a ramp exerts a support force on the piano to prevent the piano from passing through its surface. However, since the ramp isn’t exactly horizontal, that support force isn’t exactly vertical. The piano’s weight still points straight down, but since the ramp’s support force doesn’t point straight up, the two forces can’t balance one another. There is a nonzero net force on the piano. This net force can’t point into or out of the ramp. If it did, the piano would accelerate into or out of the ramp and the two objects would soon either lose contact or travel through one another. Instead, the net force points exactly along the surface of the ramp—a direction tangent or parallel to the surface. More specifically, it points directly downhill, so the piano accelerates down the ramp!
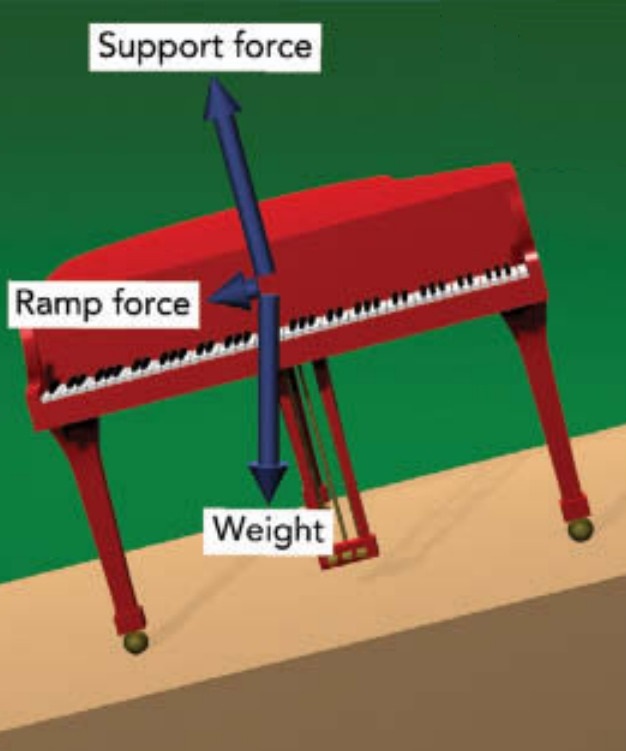
However, because this net force is much smaller than the piano’s weight, the piano’s acceleration down the ramp is slower than if it were falling freely. This effect is familiar to anyone who has bicycled downhill or watched a cup slip slowly off a tilted table. Although gravity is still responsible, these objects accelerate more slowly than they would if falling and in the direction of the downward slope.
Therein lies the beauty of the ramp. By putting the piano on a ramp, you let the ramp support most of the piano’s weight. The piano experiences only a small residual force, (ramp force), pushing it downhill along the ramp. If you now push uphill on the piano with a force that exactly balances that downhill ramp force, the net force on the piano drops to zero and the piano stops accelerating. If you push uphill a little harder, the piano will accelerate up the ramp!
The ramp provides mechanical advantage, the process whereby a mechanical device redistributes the amounts of force and distance that go into performing a specific amount of mechanical work. In moving the piano with the help of the ramp, you’ve performed a task that would normally require a large force over a small distance by supplying a small force over a large distance. You might wonder whether the ramp itself does any work on the piano; it doesn’t. Although the ramp exerts a support force on the piano and the piano moves along the ramp’s surface, this force and the distance traveled are at right angles to one another. The ramp does no work on the piano