The ramp that is only one tool that provides mechanical advantage. In this section, we’ll look at another such device: the type of lever known as a seesaw. Seesaws don’t go anywhere; they rotate.
The Seesaw
Any child who has played on a seesaw with friends of different sizes knows that the toy works best for two children of roughly the same weight. Evenly matched riders balance each other, and this balance allows them to rock back and forth easily. In contrast, when a light child tries to play seesaw with a heavy child, the heavy child’s side of the seesaw drops rapidly and hits the ground with a thud. The light child is tossed into the air.
There are several solutions to the heavy child-light child problem. Of course, two light children could try to balance one heavy child. But most children eventually realize that if the heavy child sits closer to the seesaw’s pivot, the seesaw will balance. The children can then make the seesaw tip back and forth easily, just as it does when two evenly matched children ride at its ends. This is a pretty useful trick, and we’ll explore it later in this section. First, though, we’ll need to look carefully at the nature of rotational motion.
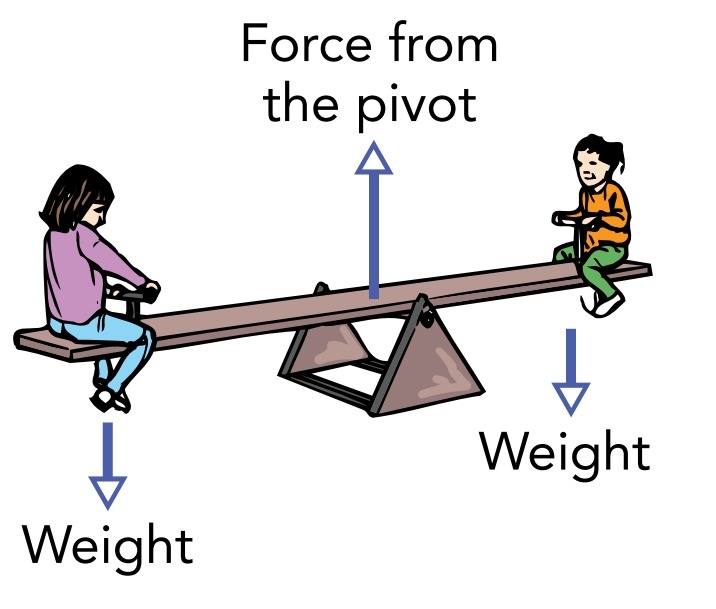
For simplicity, let’s ignore the mass and weight of the seesaw itself. There are then only three forces acting on the occupied seesaw shown in Fig.: two downward forces (the weights of the two children) and one upward force (the support force of the central pivot). Seeing those three forces, we may immediately think about net forces and begin to look for some overall acceleration of this toy and its riders. But we know that the seesaw remains where it is in the playground and isn’t likely to head off for Kalamazoo or the center of Earth anytime soon. Because the seesaw’s fixed pivot always provides just enough upward and sideways force to keep the seesaw from accelerating as a whole, the seesaw always experiences zero net force and never leaves the playground. Overall movement of an object from one place to another is called translational motion. Although the seesaw never experiences translational motion, it can turn around the pivot, and thus it experiences a different kind of motion. Motion around a fixed point (which prevents translation) is called rotational motion.
Rotational motion is what makes a seesaw interesting—the whole point of a seesaw is that it can rotate so that one child rises and the other descends.
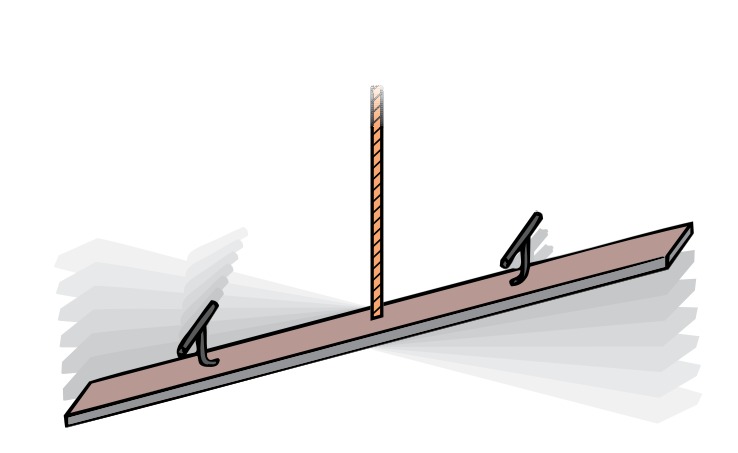
Imagine holding onto the seesaw to keep it level for a moment while the child on the left climbs off the seesaw. Now imagine letting go of the seesaw. As soon as you let go, the seesaw begins to rotate clockwise, and the child on the right descends toward the ground. The seesaw’s motion is fairly slow at first, but it moves more and more quickly until that child strikes the ground with a teeth-rattling thump. We could describe the seesaw being twisted from rest in the following way:
The seesaw starts out not rotating at all. When we release the seesaw, it begins to rotate clockwise. The seesaw’s rate of rotation increases continuously in the clockwise direction until the seesaw strikes the ground.
The Seesaw’s Center of Mass
There’s a special point in or near a free object about which all of its mass is evenly distributed and about which it naturally spins—its center of mass. The axis of rotation passes right through this point so that, as the free object rotates, the center of mass doesn’t move unless the object has an overall translational velocity. The center of mass of a typical ball is at its geometrical center, while the center of mass of a less symmetrical object depends on how the mass of that object is distributed. Center of mass allows us to separate an object’s translational motion from its rotational motion.
For example, your seesaw has been designed with its center of mass located exactly where the pivot will go. As a result, the pivot will prevent any translational motion of the installed seesaw while permitting nearly free rotational motion of the seesaw, at least about one axis. When examining rotational motion, we need to choose the pivot point or center of rotation, the point around which all the physical quantities of rotation are defined. For a free object, the natural pivot point is its center of mass. For a constrained object, the best pivot point may be determined by the constraints—a door, for example, pivots about its hinges. Since your installed seesaw will continue to pivot about its center of mass, that point will remain the best choice for the center of rotation.
If the seesaw is experiencing several torques at once, it can’t respond to them individually. Instead, it undergoes angular acceleration in response to the net torque it experiences, the sum of all the individual torques being exerted on it. There is a simple relationship between the net torque exerted on the seesaw, its rotational mass, and its angular acceleration. The seesaw’s angular acceleration is equal to the net torque exerted on it divided by its rotational mass or, as a word equation,
\[angular~acceleration = \frac{net~torque}{rotational~mass}\]
\[net torque = rotational mass \times angular acceleration\] in symbols: \[\tau_{net} = I.\alpha,\]
where, \(I\) is moment of Inertia and \(\alpha\) is angular acceleration.
and in everyday language: Spinning a marble is much easier than spinning a merry-go-round
Levers and Mechanical Advantage
When two children sit on a motionless horizontal seesaw board, each child pushes down on the board with a force equal to that child’s weight. The force is directed perpendicular to the lever arm from the pivot to the force, so it produces a torque on the board about the pivot. If the children are properly situated on opposite sides of the board, their torques cancel and the seesaw board experiences zero net torque. The seesaw is balanced. Both children still push down on the board and their torques still sum to zero. Now, however, the descending child does work on the board by pushing it downward as it moves downward, and the board does work on the rising child by pushing that child upward as the child moves upward. Because the seesaw is balanced, the work done on the board by the descending child is equal to the work done by the board on the rising child. In effect, the board transfers energy perfectly from the descending child to the rising child.
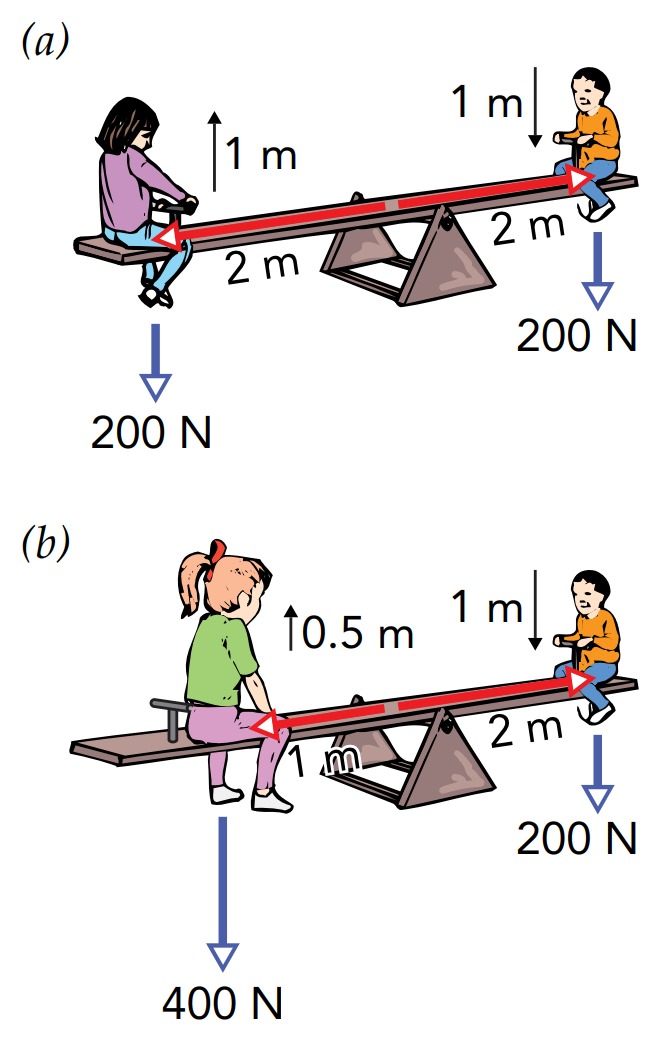
The seesaw’s mechanical advantage allows even the tiniest child sitting at its end to lift the heaviest adult sitting near its pivot. Because the child travels much farther than the adult, the child’s work on the seesaw equals the seesaw’s work on the adult. This effect—a small force exerted for a long distance on one part of a rotating system producing a large force exerted for a short distance elsewhere in that system—is an example of the mechanical advantage associated with levers.
Lever Physics
Wheels
Like ramps and levers, wheels are simple tools that make our lives easier. But a wheel’s main purpose isn’t mechanical advantage, it’s overcoming friction. Up until now, we’ve ignored friction, looking at the laws of motion as they apply only in idealized situations. However, our real world does have friction, and most objects in motion tend to slow down and stop because of it. One of our first tasks in this section will therefore be to understand friction.
Microscopic View of Friction
As the file cabinet slides by itself across the floor, it experiences a horizontal frictional force that gradually brings it to a stop. From where does this frictional force come? The obvious forces on the file cabinet are both vertical, not horizontal; the cabinet’s weight is downward, and the support force from the floor is upward. How can the floor exert a horizontal force on the file cabinet? The answer lies in the fact that neither the bottom of the file cabinet nor the top of the floor is perfectly smooth. They both have microscopic hills and valleys of various sizes. The file cabinet is actually supported by thousands of tiny contact points, where the file cabinet directly touches the floor. As the file cabinet slides, the microscopic projections on the bottom of the file cabinet pass through similar projections on the top of the floor. Each time two projections collide, they experience horizontal forces. These tiny forces oppose the relative motion and give rise to the overall frictional forces experienced by the file cabinet and floor. Because even an apparently smooth surface still has some microscopic surface structure, all surfaces experience friction as they rub across one another. Increasing the size or number of these microscopic projections by roughening the surfaces generally leads to more friction. If you put sandpaper on the bottom of the file cabinet, it would experience larger frictional forces as it slides across the floor. On the other hand, a microscopically smoother “nonstick” surface, like that used in modern cookware, would let the file cabinet slide more easily.
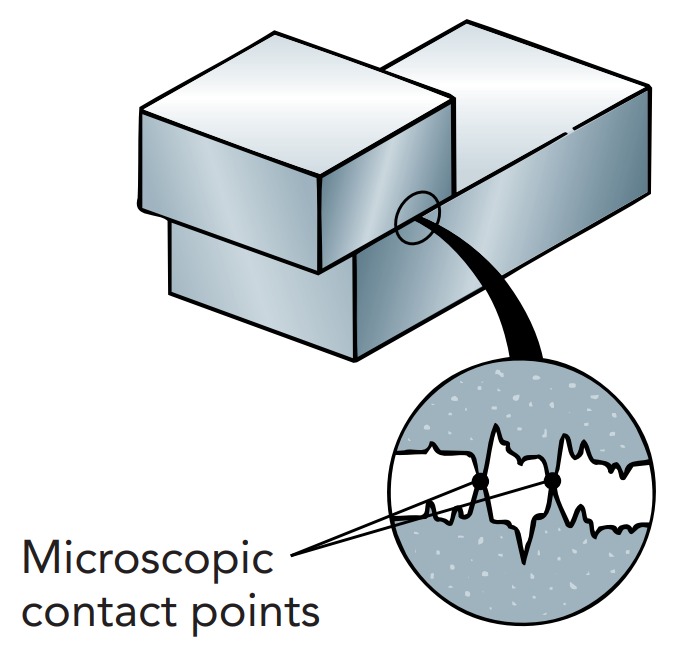
Increasing the number of contact points by squeezing the two surfaces more tightly together also leads to more friction. The microscopic projections simply collide more often. That’s why adding more sheet music to the file cabinet would make it harder to slide. Doubling the file cabinet’s weight would roughly double the number of contact points, making it about twice as hard to move across the floor. A useful rule of thumb is that the frictional forces between two firm surfaces are proportional to the forces pressing those two surfaces together.
Friction also causes wear when the colliding contact points break one another off. With time, this wear can remove large amounts of material so that even seemingly indestructible stone steps are gradually worn away by foot traffic. The best way to reduce wear between two surfaces (other than inserting a lubricant between them) is to polish them so they are extremely smooth. The smooth surfaces will still touch at contact points and experience friction as they slide across one another, but their contact points will be broad and round and will rarely break one another off during a collision.
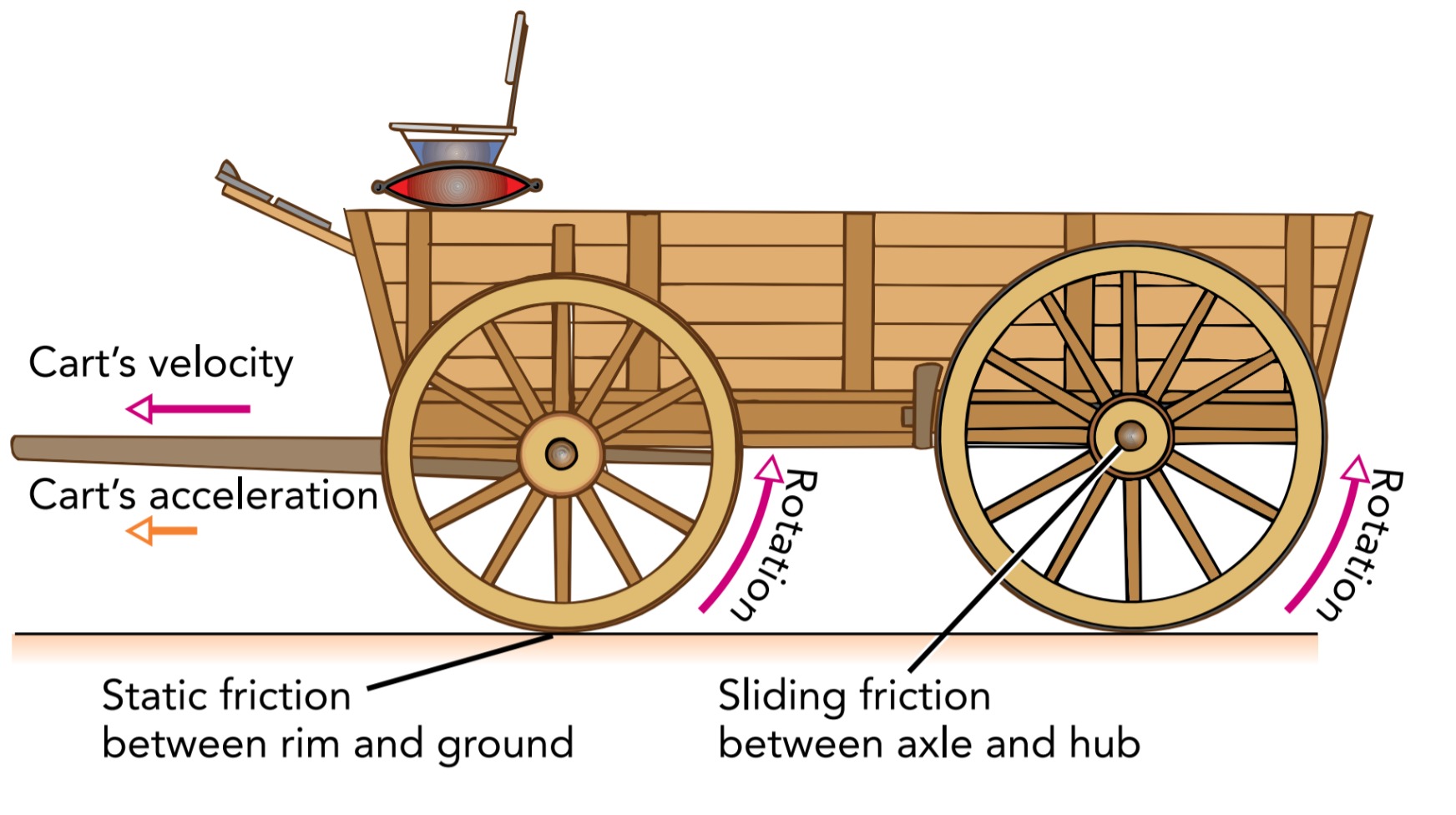
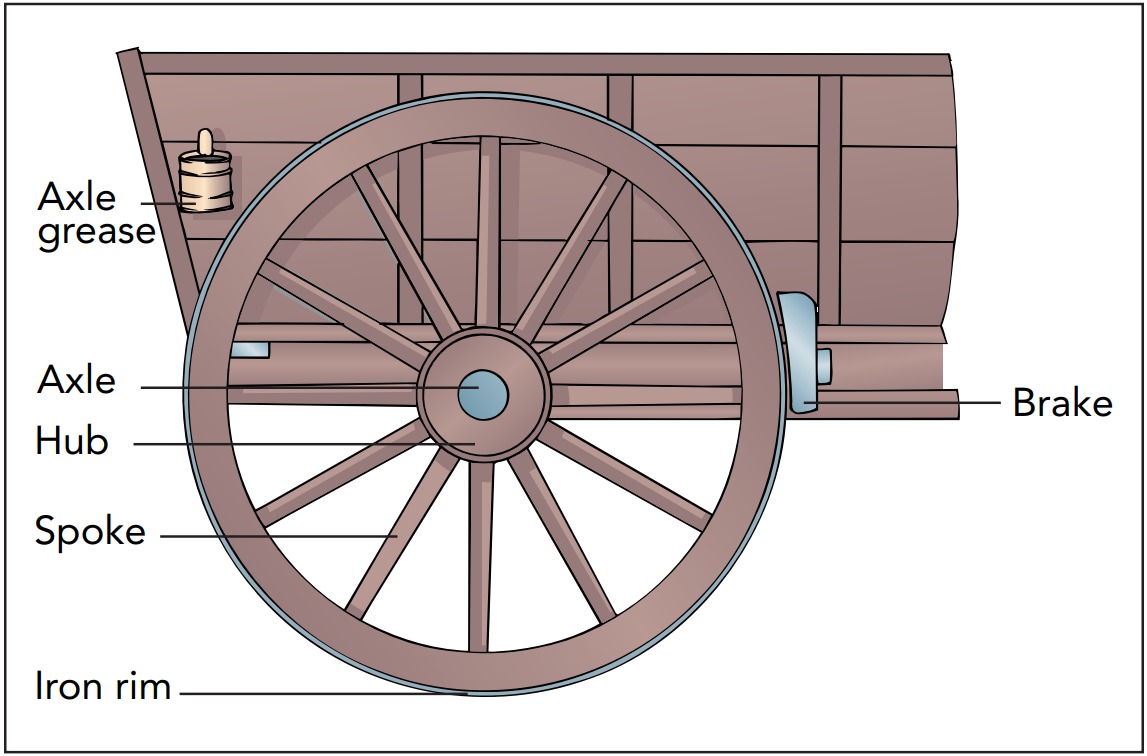
Mechanical systems can help you move one object across another without sliding. The simplest cart rests on fixed poles or axles that pass through central holes or hubs in the four wheels. The ground exerts upward support forces on the wheels, the wheels exert upward support forces on the axles, and the axles support the cart and its contents. As the cart moves forward, its wheels roll. Their bottom surfaces don’t slide or skid across the ground; instead, each wheel lowers a portion of its surface onto the sidewalk, leaves it there briefly so that it may experience static friction, and then raises it back off the sidewalk, with a new portion of wheel surface taking its place. Because of the touch-and-release character of rolling, there is no sliding friction between the cart’s wheels and the ground. Unfortunately, as each wheel rotates, its hub slides across the stationary axle at its center. This sliding friction wastes energy and causes wear to both the hub and axle. However, the narrow hub moves relatively slowly across the axle, so the work and wear done each second are small. Still, this sliding friction is undesirable and can be reduced significantly by lubricating the hub and axle with axle grease.
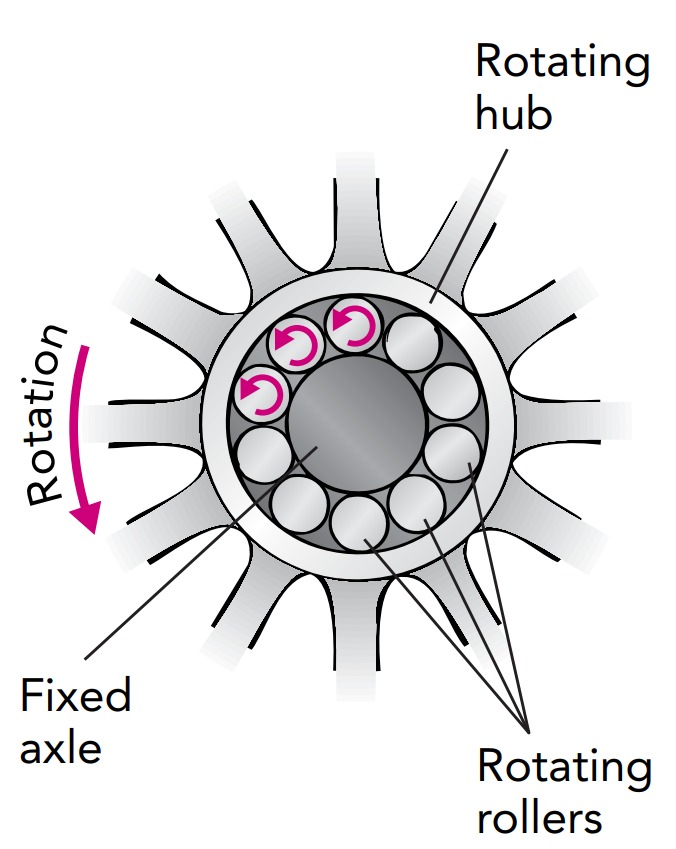
A better solution is to insert rollers between the hub and axle. The result is a roller bearing, a mechanical device that eliminates sliding friction between a hub and an axle. A complete bearing consists of two rings separated by rollers that keep those rings from rubbing against one another. In this case, the bearing’s inner ring is attached to the stationary axle, while its outer ring is attached to the spinning wheel hub. The nondriven wheels of an automobile are supported by roller bearings on essentially stationary axles. The non-driven wheels of lighter vehicles, such as bicycles and wagons, are similarly supported on stationary axles, but their bearings use balls instead of rollers—ball bearings. When a vehicle with free wheels starts forward, static friction from the ground pushes backward on the bottoms of those free wheels to keep them from skidding forward. Those frictional forces also produce torques that cause the wheels to begin turning, and they roll forward.
A car’s engine-powered or driven wheels are also supported by roller bearings, but these bearings act somewhat differently. Because the engine must be able to exert torque on each driven wheel, those wheels are rigidly connected to their axles. As the engine spins these axles, the axles spin their wheels. A bearing prevents each spinning axle from rubbing against the car’s frame. This bearing’s outer ring is attached to the stationary car frame, while its inner ring is attached to the spinning axle. When a vehicle begins to spin its driven wheels, static friction from the ground pushes forward on the bottoms of those driven wheels to keep them from skidding backward. Since those forward frictional forces are the only horizontal forces on the vehicle, the vehicle accelerates forward, and the driven wheels roll forward.