Springs
From day to day, depending on how much you eat, the amount of you stays approximately the same. But how can you tell how much that is? The best measure of quantity is mass: kilograms of gold, grain, or you. Mass is the measure of an object’s inertia and, it doesn’t depend on the object’s environment or on gravity.
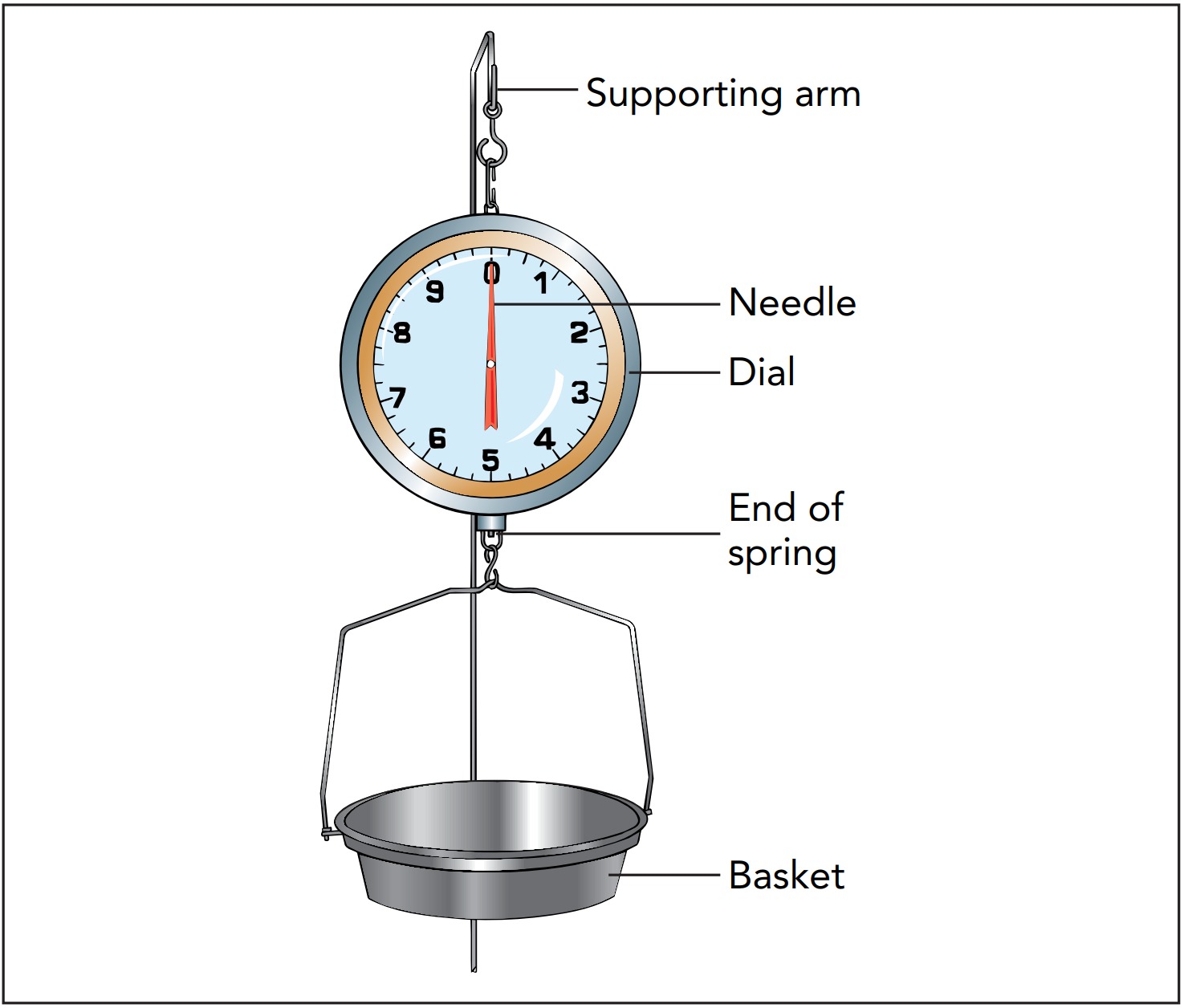
A kilogram box of cookies always has a mass of 1 kilogram, no matter where in the universe you take it. But mass is difficult to measure directly. Moreover, the very concept of mass is only about 300 years old. Consequently, people began quantifying the material in an object by measuring its weight. Spring scales eventually became one of the simplest and most practical tools for accomplishing this task, and they are still found in bathrooms and grocery stores today. They really do contain springs, although these are normally hidden from view.
When you stand on a bathroom scale, the scale doesn’t directly measure your weight. That’s because your weight is a force that Earth’s gravity exerts on you, not on the scale, so it affects the scale only indirectly. What the scale actually reports is how much upward force it exerts on you to keep you from falling. When you’re not falling or otherwise accelerating, the scale pushes you upward just as hard as your weight pulls you downward, so knowing the scale’s force on you is equivalent to knowing your weight.
That subtle difference between your weight and what the scale reports is important, however, because it makes the weighing process sensitive to acceleration. If you’re accelerating, the scale won’t report your true weight. For example, when you jump up and down on the scale, the scale’s reading varies wildly. You accelerate as you jump, so the two forces acting on you—your weight downward and the scale’s push upward— don’t sum to zero. If you want an accurate measurement of your weight, therefore, you have to stand still.
Even when you stand still, weighing is not a perfect way to quantify the amount of material in your body. That’s because your weight depends on your environment. If you always weigh yourself in the same place, the readings will be pretty consistent, as long as you don’t routinely eat a dozen jelly doughnuts for lunch. But if you moved to the moon, where gravity is weaker, you’d weigh only about one-sixth as much as on Earth. Even a move elsewhere on Earth will affect your weight: Earth bulges outward slightly at the equator, and gravity there is about 0.5% weaker than at the poles. That change, together with a small acceleration effect due to Earth’s rotation, means that a scale will read 1.0% less when you move from the north pole to the equator. Obviously, moving south is not a useful weight-loss plan.
Stretching of Spring
At the grocery store, you weigh a melon by placing it in the basket of a spring scale. Like a bathroom scale, the grocery store scale can’t measure the melon’s weight directly; instead, it reports how much upward force it exerts on the melon. As long as the melon isn’t accelerating, the scale’s upward force on the melon is equal but opposite to the melon’s weight, so measuring one force is equivalent to measuring the other.
In keeping with its name, the spring scale uses a spring to push upward on the melon. The beauty of that arrangement is that a simple relationship exists between a spring’s length and the forces it’s exerting on its ends. The spring scale determines how much upward force it’s exerting on the melon by measuring the length of its spring.
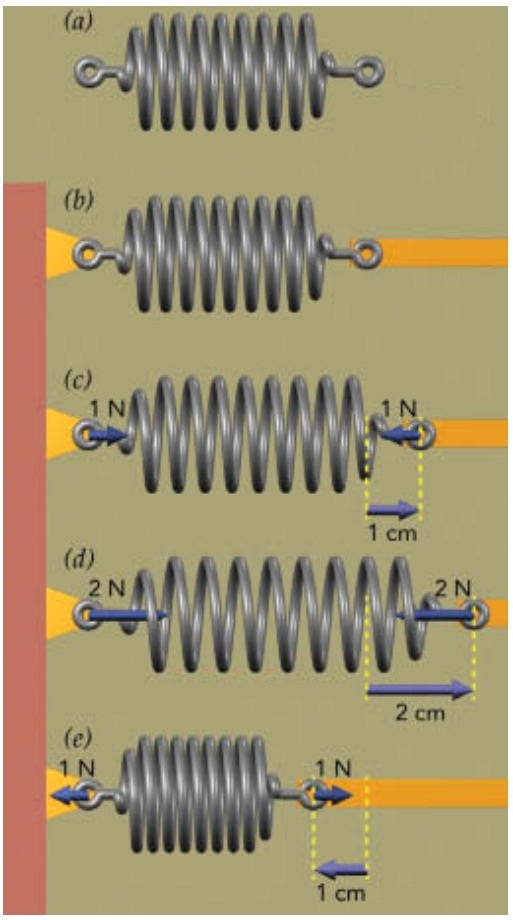
The spring shown in consists of a wire coil that pulls inward on its ends when it’s stretched and pushes outward on them when it’s compressed. When that spring is neither stretched nor compressed, it exerts no forces on its ends. If no other forces act on this relaxed spring, each end is in equilibrium—it experiences zero net force. As the phrase zero net force suggests, equilibrium occurs whenever the forces acting on an object sum to zero so that the object doesn’t accelerate. When you sit motionless in a chair, for example, you are in equilibrium. The relaxed spring is also at its equilibrium length, its natural length when you leave it alone. No matter how you distort this spring, it tries to return to this equilibrium length. The stretched spring now exerts a leftward force on that end, trying to restore it to its original equilibrium position. Because the force that the spring exerts on its end acts to restore that end to equilibrium, we call it a restoring force. The spring actually exerts restoring forces on both of its ends, pulling them equally hard in opposite directions. Remarkably, that restoring force is exactly proportional to how far the the spring is has stretched. The compressed spring exerts a outward force towards its end. Nonetheless, that force is still a restoring force and it is still proportional to the spring’s distortion. In general, whenever a spring is distorted away from its equilibrium length, it exerts a restoring force on its moveable end that is proportional to the distortion and points in the opposite direction. This observation is expressed in Hooke’s law, named after the Englishman Robert Hooke, who discovered it in the late seventeenth century. This law can be written in a word equation:
\[restoring force = −spring constant \times distortion\]
in symbols:
\[F = −k \times x,\]
and in everyday language:
The stiffer the spring and the farther you stretch it, the harder it pulls back.
Here the spring constant, \(k\), is a measure of the spring’s stiffness.
The larger the spring constant—that is, the firmer the spring—the larger the restoring force the spring exerts for a given distortion. The negative signs in these equations indicate that a restoring force always points in the direction opposite the distortion. Springs are distinguished by their stiffness, as measured by their spring constants. Some springs are soft and have small spring constants—for example, you need just one finger to compress the spring in your retractable ballpoint pen. Other springs, like the large ones that suspend an automobile chassis above the wheels, are firm and have large spring constants. But no matter the stiffness, nearly all simple springs obey Hooke’s law.
Hooke’s law is remarkably general and isn’t limited to the behavior of coil springs. Many objects respond to distortion with restoring forces that are proportional to how far you’ve distorted them away from their equilibrium lengths—or, in the case of some complicated objects, their equilibrium shapes. Equilibrium shape is the shape an object adopts when it’s not subject to any outside forces. If you bend a tree branch, it will push back with a force proportional to how far it has been bent. If you pull on a rubber band, it will pull back with a force proportional to how far it has been stretched, up to a point. If you squeeze a mattress, it will push outward with a force proportional to how far it has been compressed. If a heavy truck bends a bridge downward, the bridge will push upward with a force proportional to how far it has been bent.
There is a limit to Hooke’s law, however. If you distort an object too far, it will usually begin to exert less force than Hooke’s law demands. This is because you will have exceeded the object’s elastic limit and will have deformed it permanently in the process. If you stretch a spring too far, it won’t return to its original equilibrium length when you release it; if you bend a tree branch too far, it will break. As long as you stay within the elastic limit, however, a great many things obey Hooke’s law—a rope, a ruler, a tabletop, and a trampoline.
Distorting a spring requires work. When you stretch a spring with your hand, pulling its ends apart as they move apart, you transfer some of your energy to the spring. The spring stores this energy as elastic potential energy. If you reverse the motion, the spring returns most of this energy to your hand; the remainder is converted to thermal energy by frictional effects inside the spring itself. Work is also required to compress, bend, or twist a spring. In short, a spring that is distorted away from its equilibrium shape always contains elastic potential energy.
It contains a coil spring that’s responsible for the weighing process. One end of that spring is suspended from the ceiling, and the other end supports the weighing basket. For the sake of simplicity, let’s suppose the spring and the basket have negligible weights and that the basket is effectively the bottom end of the spring. With the basket empty, the spring adopts its equilibrium length and the basket is in a position of stable equilibrium. If you shift the basket up or down and then let go of it, the spring will push it back to this position. When you place a melon in the basket, the melon’s weight pushes the basket downward and spoils its equilibrium. The basket starts descending and as it does, the spring stretches and begins to exert an upward force on the basket. The more the spring stretches, the greater this upward force so that eventually the spring is stretched just enough so that its upward restoring force exactly supports the melon’s weight. The basket is now in a new stable equilibrium position—again experiencing zero net force. The scale, then, uses Hooke’s law to determine the weight of the melon. When the basket has settled at its new equilibrium position, where the melon’s downward weight is exactly balanced by the spring’s upward restoring force, the amount the spring has stretched is an accurate measure of the melon’s weight.
The scales differ only in the way they measure how far the spring has stretched beyond its equilibrium length. The scale uses a pointer attached to the end of the spring, while, the scale uses a rack and pinion gear system that converts the small linear motion of the stretching spring into a much more visible rotary motion of the dial needle. The rack is the series of evenly spaced teeth attached to the lower end of the spring; the pinion is the toothed wheel attached to the dial needle. As the spring stretches, the rack moves downward, and its teeth cause the pinion to rotate. The farther the rack moves, the more the pinion turns and the higher the weight reported by the needle.
Each of these spring scales reports a number for the weight of the melon you put in the basket. For that number to mean something, the scale has to be calibrated. Calibration is the process of comparing a local device or reference to a generally accepted standard to ensure accuracy. To calibrate a spring scale, the device or its reference components must be compared against standard weights. Someone must put a standard weight in the basket and measure just how far the spring stretches. Each spring is different, although spring manufacturers try to make all their springs as identical as possible.
Spring Physics
Bouncing Ball
If you visit a toy or sporting goods store, you’ll find many different balls—almost a unique ball for every sport or ball game. These balls differ in more than just size and weight. Some are very hard, others very soft; some are smooth, others rough or ridged. A bouncy ball, for example, bounces extraordinarily well, while a foam rubber ball hardly bounces at all. Even balls that appear identical can be very different; a new tennis ball bounces much better than an old one.
The Way the Ball Bounces
What would sports be like without balls? Basketball, baseball, tennis, golf, soccer, volleyball … the list of sports that depend on them is almost endless—and nearly all those ball sports involve bouncing. While most bounces are obvious, others are more subtle. When a baseball hits a bat or a player kicks a soccer ball, those balls are actually bouncing, albeit from moving objects. Why does a ball bounce, and how do its characteristics and circumstances affect its bounce?
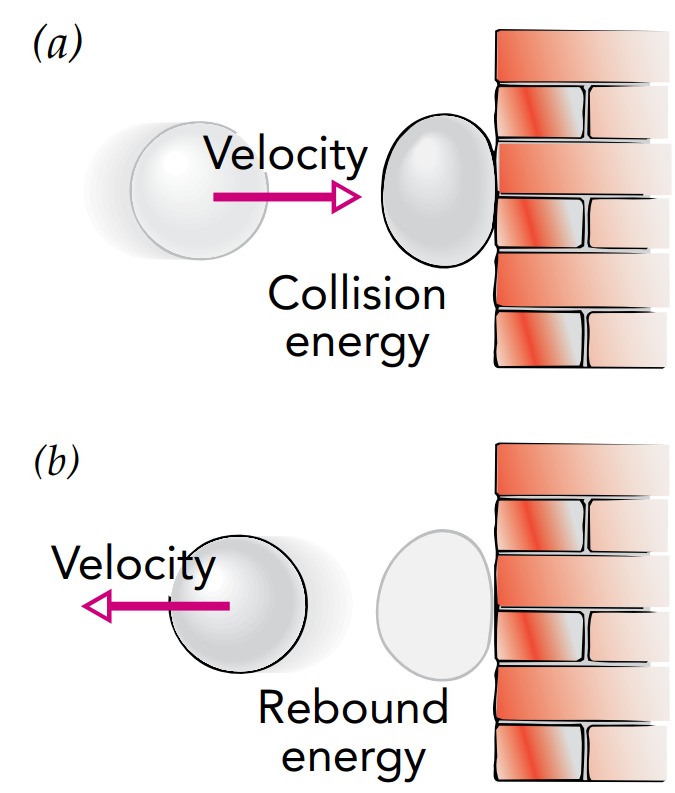
We’ll start by looking at a ball’s shape. When nothing pushes on the ball, it adopts its equilibrium shape, typically a sphere. Both balls and springs store energy as you distort them away from their equilibrium shapes and release that stored energy when you let them return to their equilibrium shapes.
This energy storage and return is evident when a ball bounces off a hard surface. As those two objects collide, the ball’s surface distorts and its elastic potential energy increases. The energy responsible for that distortion is extracted from the kinetic energies of the colliding objects. As the two objects subsequently rebound, the ball’s surface returns toward its equilibrium and its elastic potential energy decreases. That return to equilibrium releases energy that is added to the kinetic energies of the rebounding objects. We’ll call the kinetic energy absorbed during the collision the collision energy and the kinetic energy released during the rebound the rebound energy. In fact, the two energies would be equal except for one important detail: the two objects have changed. Their thermal energies have increased. As it distorts and then returns to equilibrium, the ball wastes some of the collision energy as thermal energy, so the rebound energy is always less than the collision energy. While total energy is conserved during the bounce, individual forms of energy are not. No physical law prevents kinetic energy from becoming thermal energy, and it happens every bounce.
TABLE: Approximate Energy Ratios and Speed Ratios for a Variety of Balls
| Rebound Energy | Rebound Speed† | |
|---|---|---|
| Type of Ball | Collision Energy | Collision Speed |
| Superball | 0.81 | 0.90 |
| Racquet ball | 0.72 | 0.85 |
| Golf ball | 0.67 | 0.82 |
| Basketball | 0.64 | 0.80 |
| Tennis ball | 0.56 | 0.75 |
| Steel ball bearing | 0.42 | 0.65 |
| Baseball | 0.30 | |
| Foam rubber ball | 0.09 | 0.30 |
| “Unhappy” ball | 0.01 | 0.10 |
| Beanbag | 0.002 | 0.04 |
† Known as the coefficient of restitution, this speed ratio can be squared to obtain the energy ratio.
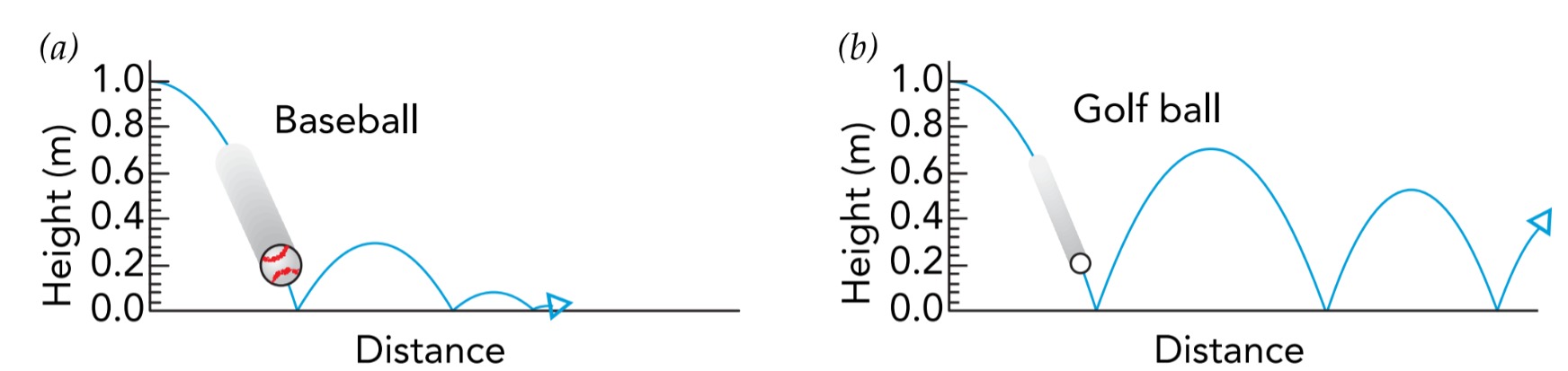
Some balls bounce better than others. A bouncy ball is often called “lively,” and a ball that doesn’t bounce well is said to be “dead.” A lively ball is extremely elastic—it converts most of the collision energy into elastic potential energy during the collision and converts most of that elastic potential energy into rebound energy during the rebound. A dead ball, on the other hand, is barely elastic at all—it converts most of the collision energy into thermal energy during the collision and converts most of what’s left into thermal energy during the rebound.
The ratio of rebound energy to collision energy (Table) determines how high a ball will bounce when you drop it from rest onto a hard floor. Before you drop it, the ball has only gravitational potential energy, which is proportional to its height above the floor. That potential energy becomes kinetic energy as the ball falls and then collision energy when it collides with the floor. The ball’s rebound energy becomes kinetic energy as it rebounds from the floor and then gravitational potential energy as it rises. At its peak, the ball has only gravitational potential energy, which is again proportional to its height. The ratio of the ball’s rebound energy to its collision energy is therefore equal to the ratio of its final height to its initial height. For an ideally elastic ball, these ratios are 1.00; all the collision energy is returned as rebound energy and the ball rebounds to its initial height. Known as elastic collisions, such perfect bounces are common among the tiny atoms in a gas but are unattainable for ordinary objects; there are just too many ways for any large item to divert or dissipate energy, including as thermal energy, sound, vibration, and light.
A real ball experiences inelastic collisions—it wastes some of the collision energy as thermal energy and rebounds to a lesser height. For example, a baseball’s rebound energy is only 0.30 times its collision energy, so it will rebound to only 30% of its original height. Without that dramatic energy loss during a bounce, baseball pitchers would need to wear armor.
While that energy ratio is useful, a ball is traditionally characterized by a speed ratio: its rebound speed divided by its collision speed. Here, the collision speed is how fast the two objects approach one another before the bounce, and the rebound speed is how fast those objects separate after the bounce. The speed ratio is known as the ball’s coefficient of restitution:
\[coefficient ~of~ restitution = \frac{rebound~ speed~ of~ ball}{ collision ~speed~ of~ ball} \]
The larger a ball’s coefficient of restitution, the faster it rebounds from a surface for a given collision speed. For example, a basketball’s coefficient of restitution is 0.80, so when it bounces off the backboard during a foul shoot, its rebound speed is only 0.80 times its collision speed. That decrease in speed makes it easier for the ball to drop into the basket after it bounces than before it bounces.
Since a ball’s kinetic energy is proportional to the square of its speed, its energy ratio is simply the square of its speed ratio.
Balls bounce best when they store energy through compression rather than through surface bending. That’s because most ball materials, such as leather or leather-like plastics, experience lots of wasteful internal friction during bending. Since solid balls involve compression, they usually bounce well, whether they’re made of rubber, wood, plastic, or metal. Air-filled balls, however, bounce well only when properly inflated. A normal basketball, which stores most of its energy in its compressed air, has a high coefficient of restitution. In contrast, an underinflated basketball, which experiences lots of surface bending during a collision, barely bounces at all. Similarly, a tennis ball bounces best when new; after a while, the compressed air inside leaks out, and the ball’s coefficient of restitution drops.
Bouncing Ball - Physics
Carousels and Roller Coasters
As your sports car leaps forward at a green light, you’re pressed firmly back against your seat. It feels as though gravity were somehow pulling you down and backward at the same time. It’s not gravity pulling backward on you, though; it’s your own inertia trying to prevent you from accelerating forward with the car. When this happens, you’re experiencing the feeling of acceleration. We encounter this feeling many times each day, whether through turning in an automobile or riding up several floors in a fast elevator. Nowhere are the feelings of acceleration more acute than at the amusement park. We accelerate up, down, and around on the carousel, back and forth in the bumper cars, and left and right in the scrambler. The ultimate ride, of course, is the roller coaster, which is one big, wild experience of acceleration. When you close your eyes on a straight stretch of highway, you can hardly tell the automobile is moving. When you close your eyes on a roller coaster, however, you have no trouble feeling every last turn in the track. It’s not the speed you feel, but the acceleration. What is often called motion sickness should really be called acceleration sickness.
Carousels and Acceleration
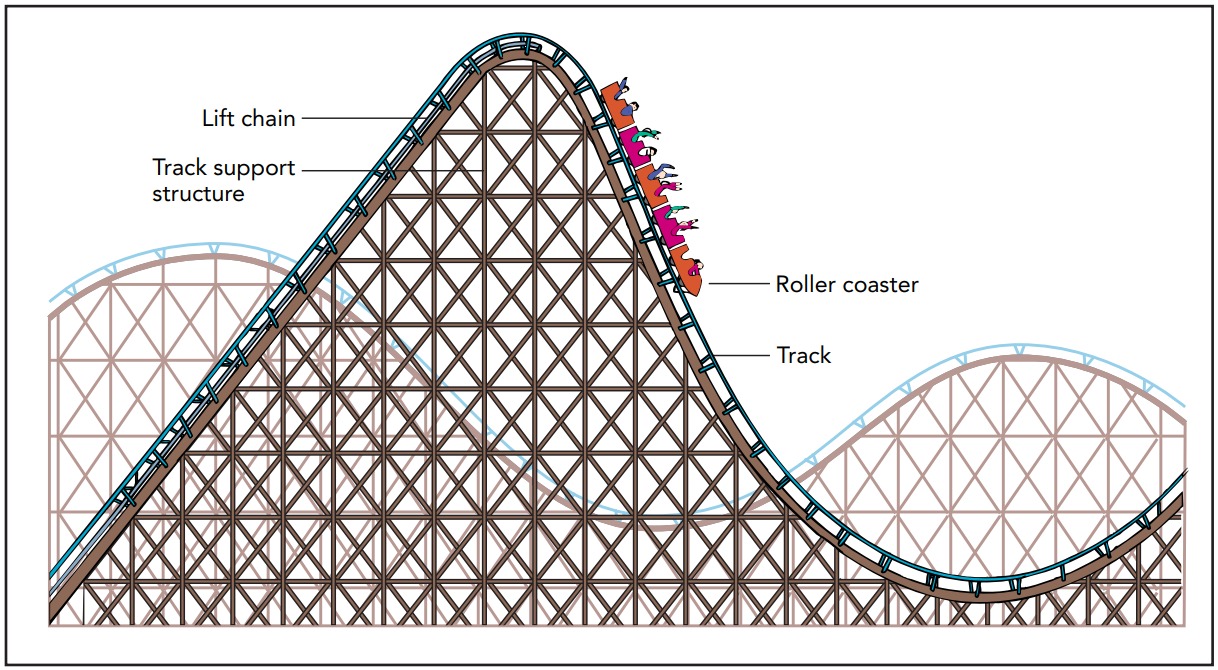
While roller coasters offer interesting visual effects, such as narrowly missing obstacles, and strange orientations, such as running upside down, the real thrill of roller coasters comes from their accelerations. Plenty of other amusement park rides suspend you sideways or upside down so that you feel ordinary gravity pulling at you from unusual angles. But why pay for those when you can stand on your head for free? For a real thrill, you need acceleration to give you the weightless feeling you experience as a roller coaster dives over its first big hill or the intense heaviness you feel as it whips you around a sharp corner. Why do accelerations give rise to these wonderful sensations, and why are they most extreme when you’re sitting in the last car of the roller coaster?

When you ride on a carousel, you travel in a circular path around a central pivot. That’s not the motion of an object that’s simply coasting forward and exhibiting inertia. If you were experiencing zero net force, you would travel in a straight line at a steady pace in accordance with Newton’s first law. However, since your path is circular instead of straight, your direction of travel is changing; you are accelerating and must be experiencing a nonzero net force. Remarkably, you are always accelerating toward the center of the circle. The person sitting in the carousel is always trying to go in a straight line, but the carousel keeps pulling him inward so that he accelerates toward the central pivot. The person is experiencing uniform circular motion. Uniform means that the person is always moving at the same speed, although his direction keeps changing. Circular describes the path the person follows as he moves, his trajectory. An acceleration of this type, toward the center of a circle, is called a centripetal acceleration and is caused by a centrally directed force, a centripetal force. A centripetal force is not a new, independent type of force like gravity but the net result of whatever forces act on the object. Centripetal means “center-seeking,” and a centripetal force pushes the object toward that center. The carousel uses support forces and friction to exert a centripetal force on the boy, and he experiences a centripetal acceleration. Amusement park rides often involve centripetal acceleration.
We can also determine the boy’s acceleration from the carousel’s angular speed and its radius. The faster the carousel turns and the larger the radius of the boy’s circular trajectory, the more he accelerates. His acceleration is equal to the square of the carousel’s angular speed times the radius of his path. We can express these two relationships as word equations:\[ acceleration = \frac{speed^{2}} {radius} = angular speed^{2} \times radius\]
in symbols:
\[a = \frac{v^{2}} {r} = \omega_{2} \times r\],
and in everyday language:
Making a tight, high-speed turn involves lots of acceleration.
Roller Coaster Acceleration
We’re now prepared to look at a roller coaster and understand what you feel when you go over hills and loop-the-loops. Every time the roller coaster accelerates, you experience a feeling of acceleration in the direction opposite your acceleration. That feeling of acceleration gives you an apparent weight that’s different from your actual weight.

A rapid horizontal accelerations tip your apparent weight in the direction opposite your acceleration. A roller coaster, however, can do something a car normally can’t—it can accelerate downward! In that case, the feeling of acceleration you experience is upward and opposes your downward feeling of weight. The two feelings at least partially cancel, so that your apparent weight points weakly downward or perhaps, if the downward acceleration is fast enough, points upward.
There is one more possibility: if you accelerate downward at just the right rate, your upward feeling of acceleration will exactly cancel your downward feeling of weight. Your apparent weight will then be zero, and you’ll feel perfectly weightless. When you’re falling, you feel perfectly weightless. Your apparent weight is zero, and nothing is supporting you. Because your hat and sunglasses are falling with you, nothing is supporting them, either. If they come off your head, they will hover around you as you all fall together.
Similarly, your internal organs don’t need to support one another as they fall, and the absence of internal support forces gives rise to the exhilarating sensation of free fall. Our bodies are very sensitive to even partial weightlessness, and this falling sensation is half the fun of a roller coaster. An astronaut falling freely in space has this disquieting weightless feeling for days on end. No wonder astronauts have such frequent troubles with motion (or, rather, acceleration) sickness.
Because a roller coaster is attached to a track, however, its rate of downward acceleration can actually exceed that of a freely falling object. In those special situations, the track will be assisting gravity in pushing the roller coaster downward. As a rider, you’ll be pushed downward, too, and your apparent weight will point upward, as though the world had turned upside down. What about a roller coaster with more than one car? For the most part, the same rules apply. However, new forces now act on each car—forces exerted by the other cars in the train. The effects of these cars are most pronounced at the top of the first and biggest hill. As the train disconnects from the lift chain and approaches the descent, it is rolling forward slowly and the first cars are well over the crest of the hill before they pick up much speed. They’re pulling hard on the cars behind them, and those cars are pulling back, slowing their descent. By the time the train is moving fast, the first car is well down the hill and the track is beginning to turn upward. The first car’s riders experience mostly upward acceleration and downward feeling of acceleration. That’s why riders in the first few cars of a roller coaster don’t feel much weightlessness.In contrast, the last car is moving at high speed early in its descent. It undergoes a dramatic downward acceleration as it’s yanked over the crest of the first hill by the cars in front of it. As a result, its riders experience large upward feelings of acceleration and quite extreme weightlessness. In fact, the designers of the track must be careful not to make the downward acceleration too rapid or the roller coaster will flick the riders in the last car right out of their seats. Each time the last car crests a hill, it accelerates downhill in a way that no other car on the coaster can match.
Obviously, it does matter where you sit on a roller coaster. The first seat offers the most exciting view, but it provides less than spectacular weightless feelings. The last car almost always offers the best weightless feelings. Probably the dullest seat in the roller coaster is the second; it offers a relatively tame ride and an unchanging view of the people in the front seat.