Introduction
The objects in this section we will be discussing on the objects like (1) bicycles and (2) rockets. In Bicycles, we see how motion and clever design can make an apparently unstable vehicle stable enough to ride easily, even without your hands on the handlebars. In Rockets and Space Travel, we look at the principle of action and reaction, and see how this basic idea makes it possible for spacecraft to leave Earth’s surface and even travel toward the stars.
In Bicycles, we learn about dynamic stability and explore issues that waiters, water-skiers, and warehouse clerks must deal with all the time. We also encounter gyroscopes and their peculiar responses to torques. In Rockets and Space Travel, we see how gravity causes objects to orbit one another, giving rise to the intricate motions of the planets, moons, and comets. We also look at new physics that appears near the extremes of speed and gravity.
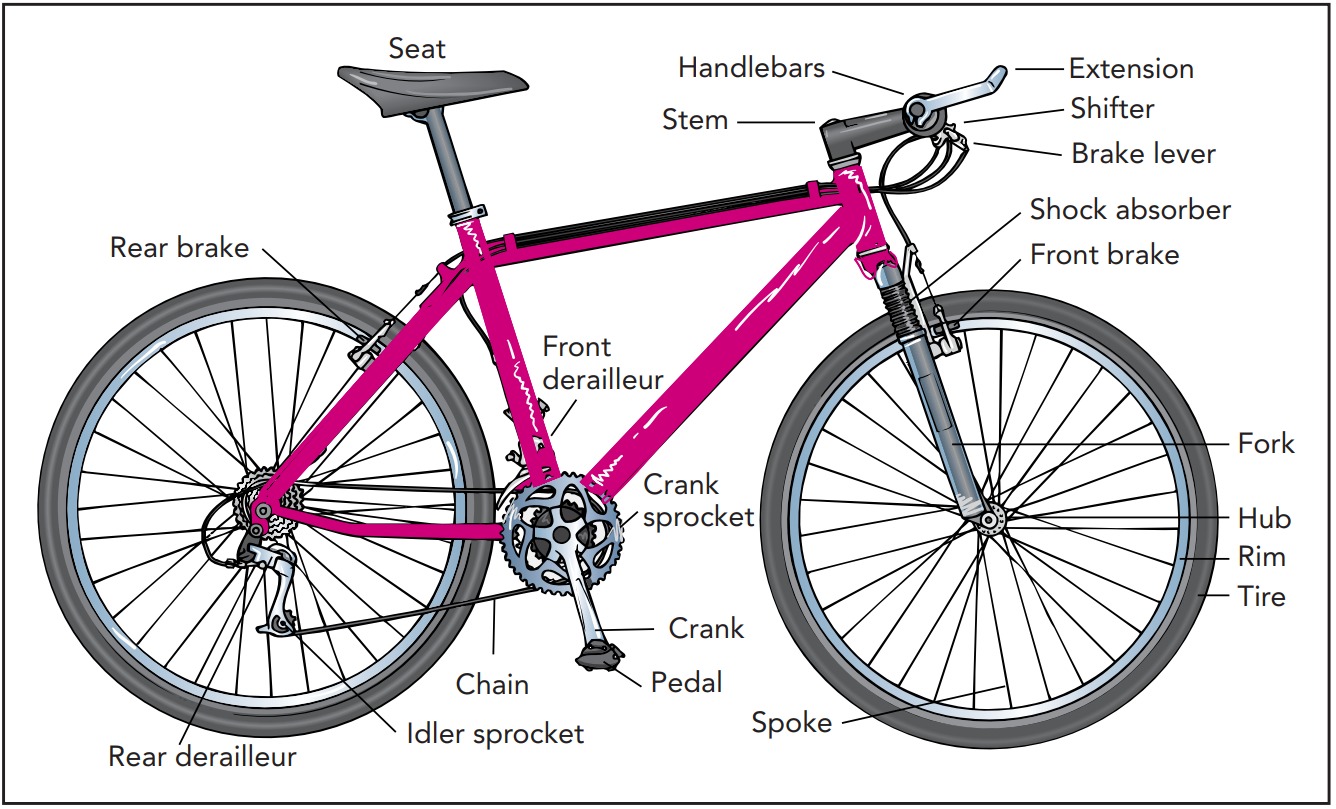
Bicycle
A bicycle is a wonderfully energy-efficient, human-powered vehicle. Its wheels allow its rider to coast forward easily on level surfaces and accelerate effortlessly down hills. Compare the easy motion of a bicycle to that of walking, which requires effort every step of the way. Bicycles are very simple machines, and most of their moving parts are quite visible: the pedals, sprockets, brakes, and steering mechanisms, to name a few. Their simplicity and visibility make bicycles relatively easy to fix, even for a novice.
Bicycles have a stability problem. With only two wheels to support them, stationary bicycles tip over easily. Why then do we use two-wheeled bicycles for transportation?
Static stability is the stability of an objects at rest. To have static stability, an object needs a stable equilibrium. Equilibrium means zero net force or torque, but near a stable equilibrium an object experiences restoring influences—forces and/or torques—that push it back toward that equilibrium. Aided by such influences, a statically stable object returns to its stable equilibrium after being displaced slightly.
A marble in a bowl exhibits static translational stability—when displaced from its equilibrium position at the bottom of the bowl, it experiences restoring forces that act to return it to the bottom of the bowl. In contrast, a stool exhibits static rotational stability—when displaced from its upright equilibrium orientation it experiences restoring torques that act to return it to upright.
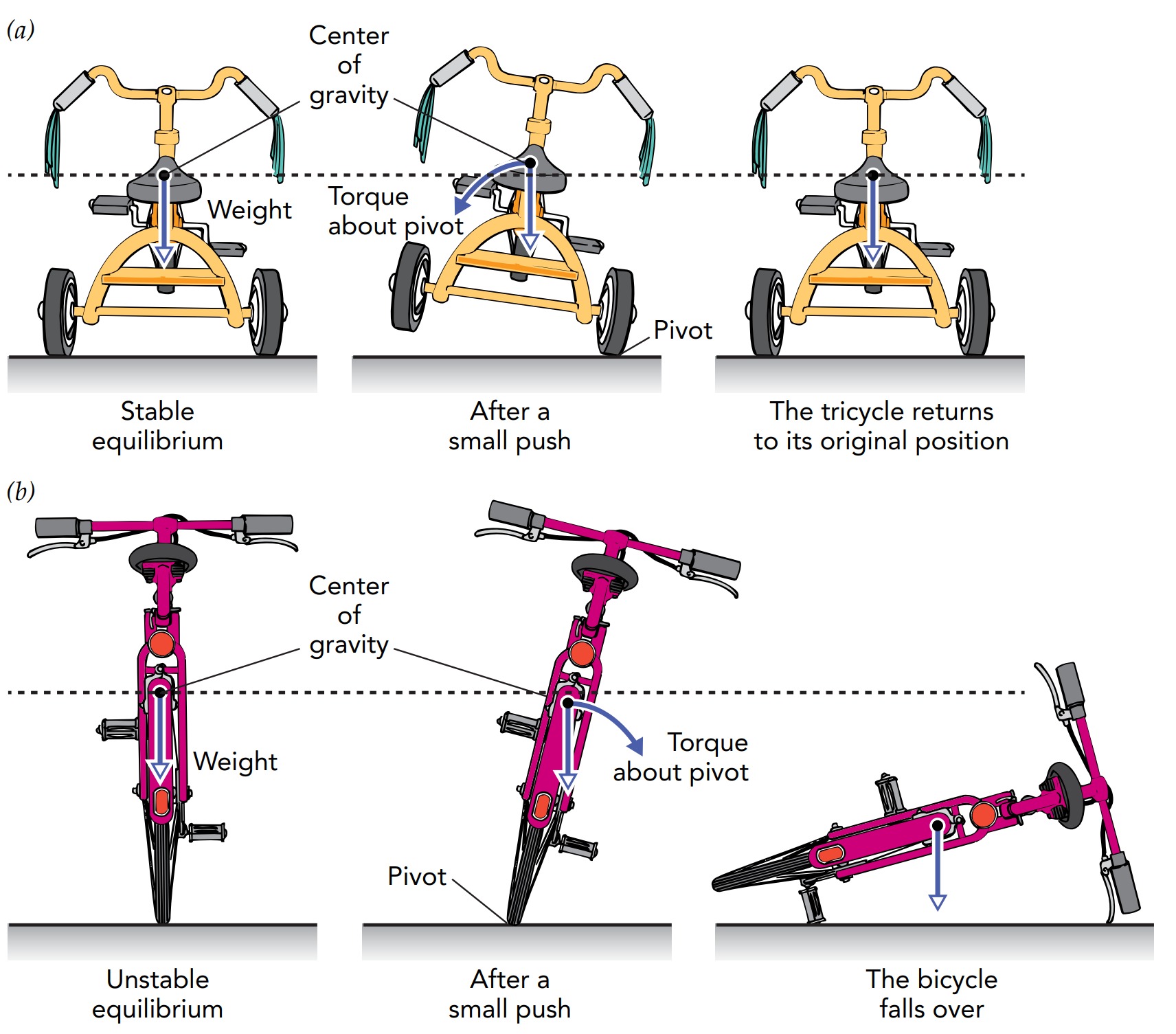
An upright tricycle has static rotational stability because it experiences restoring torques following a tip. But, bicycles don’t exhibit static translational or rotational stability.
an object accelerates in whichever direction reduces its total potential energy as quickly as possible. In this case, the tricycle undergoes angular acceleration in whichever rotational direction reduces its total potential energy as quickly as possible. Since small tips always raise the tricycle’s center of gravity and thus increase its gravitational potential energy, the tipped tricycle can reduce its total potential energy by rotating back to upright. The upright tricycle is thus in a stable rotational equilibrium—it will return spontaneously to that upright equilibrium after being tipped slightly.
No wonder children love tricycles!. This relationship between static stability and total potential energy is universal. That useful rule applies not only to static rotational stability and tricycles but also to static translational stability and everything from canoes to bridge spans to decorative mobiles. If you want an object to be stable at rest, ensure that any small displacement increases its total potential energy.
That general observation underlies a simple rule of thumb: an object resting on a surface is in a stable rotational equilibrium if a vertical line passing through its center of gravity also passes through the interior of its base of support—the polygon defined by its contact points with the ground. This rule follows from geometry: if a vertical line through the object’s center of gravity passes within its base of support, then tipping it always raises its center of gravity and increases its gravitational potential energy. Assuming that no other potential energies are significant, the tipped object will undergo angular acceleration back toward its original orientation, making that orientation a stable rotational equilibrium.
Geometry also sets the limits of the object’s static rotational stability. If the vertical line passing through its center of gravity also passes through the edge of its base of support, there are three possibilities. If its center of gravity is below the edge, the object is in a stable rotational equilibrium. If its center of gravity is exactly on the edge, the object is in a neutral equilibrium—it remains in rotational equilibrium even when you tip it about that edge.
If the object’s center of gravity is above the edge, however, it is in an unstable equilibrium—that is, when displaced slightly in certain directions, the object will experience anti-restoring torques that cause angular acceleration away from equilibrium. Tipping the object in those directions lowers its center of gravity and decreases its gravitational potential energy, so it undergoes angular acceleration away from equilibrium and tips over. If the rider of a tricycle leans out so far that their combined center of gravity is located above the edge of the triangular base of support, they’ll be in an unstable equilibrium and in danger of tipping over.
A bicycle has no stable equilibrium. Its base of support is a line defined by its two wheels and a line has only an edge, no interior. Although the rider of a bicycle can achieve rotational equilibrium by locating their combined center of gravity above that edge. As such, the bycycle is in unstable equilibrium and the slightest displacement to the side will tip them over.
Bicycles and Dynamic Stability
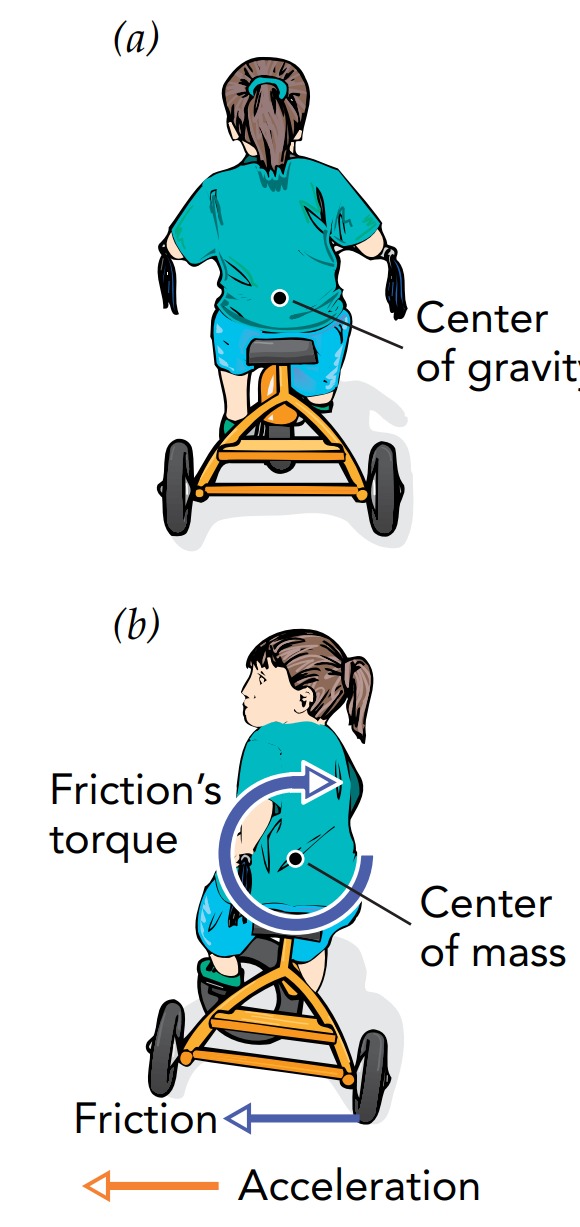
Static rotational stability matters most to people who have difficulty balancing. That’s why children learn to ride tricycles first. But when a tricycle is moving, static rotational stability doesn’t guarantee safety. If a child rolls down a steep hill and then makes a sudden sharp turn, he or she will probably flip over.
The tricycle flips because it can’t handle the enormous torque that friction exerts on it during a sharp turn. Because the horizontal frictional force that turns the tricycle is exerted well below the tricycle and rider’s combined center of mass, it produces a torque about that center of mass. If this torque is small, the tricycle’s static rotational stability will provide enough restoring torque in the opposite direction to prevent any angular acceleration. If the turn is too sharp, the huge frictional torque will overwhelm the limited restoring torque and the tricycle and rider will flip over. During high-speed turns, the tricycle is dynamically unstable.
while a bicycle lacks static stability, a moving bicycle is remarkably stable. Its dynamic stability is so good that it’s almost hard to tip over and can even be ridden without any hands on the handlebars.
As British physicist David Jones discovered, the bicycle’s incredible dynamic stability results from its tendency to steer automatically in whatever direction it’s leaning. For example, if the bicycle begins leaning to the left, the front wheel will automatically steer toward the left so as to return the bicycle to an upright position. Although a stationary bicycle falls over when it’s displaced from its unstable equilibrium, a forward-moving bicycle naturally drives under the combined center of mass and returns to that unstable equilibrium.
There are two physical mechanisms acting together to produce this automatic steering effect: one involving rotation and one involving potential energy. The first is based on the wheels alone: they behave as gyroscopes. Because each wheel is spinning, it has angular momentum and tends to continue spinning at a constant angular speed about a fixed axis in space. Since a wheel’s angular momentum can be changed only by a torque, it naturally tends to keep its upright orientation.
It prompts the bicycle to steer automatically by way of gyroscopic precession, the pivoting of a gyroscope’s rotational axis caused by a torque exerted perpendicular to its angular momentum. When a bicycle is upright, the pavement’s upward support force points toward the front wheel’s center of mass and produces no torque on that wheel. But when the bicycle leans to the left, the pavement’s upward support force no longer points at the wheel’s center of mass and it therefore produces a torque on the wheel. That torque is perpendicular to the wheel’s angular momentum, so the wheel precesses; its axis of rotation pivots toward the left and thereby steers the bicycle to safety
Assisting gyroscopic precession in this automatic steering process is a second effect due to potential energy. Because of the shape and angle of the fork supporting its front wheel, a leaning bicycle can lower its center of gravity and reduce its total potential energy by steering its front wheel in the direction that the bicycle is leaning. When the bicycle leans to the left, its front wheel steers toward the left to reduce the bicycle’s total potential energy as quickly as possible. Once again the bicycle automatically steers in the direction that it’s leaning and avoids falling over. These self-correcting effects explain why a riderless bicycle stays up so long when you roll it forward or down a hill.
Leaning While Turning
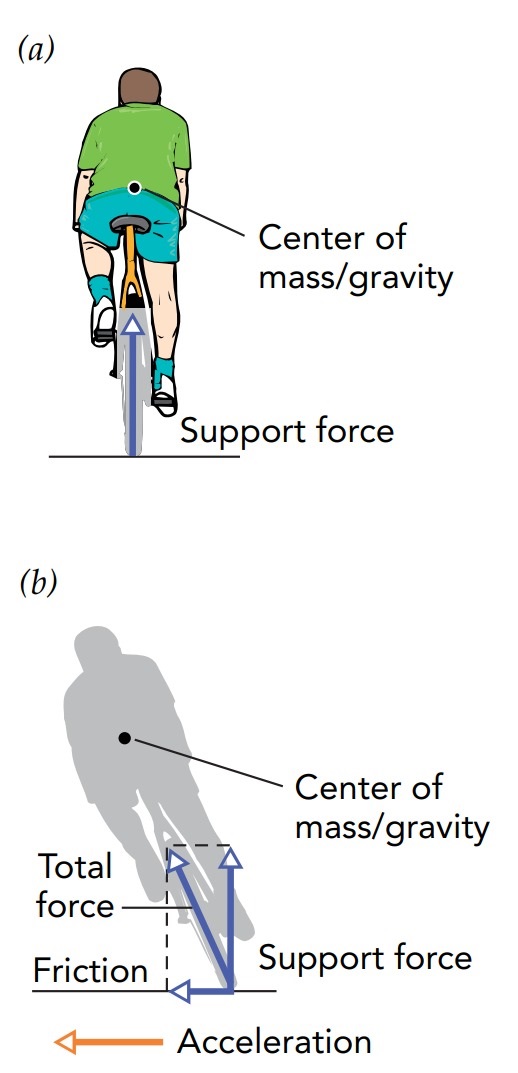
leaning can balance out the torque that friction exerts on him during the turn, the same frictional torque that flipped our unfortunate tricycle rider. With the proper lean, the bicyclist can safely complete even the sharpest turn.
As he rides along, the bicyclist tries to keep himself and the bicycle in rotational equilibrium. Since they experience a frictional torque about their combined center of mass each time they turn, the bicyclist balances that torque by leaning them toward the inside of the turn. The pavement’s upward support force then produces a torque on them about their center of mass that opposes the frictional torque. When those two torques sum to zero, the bicyclist and bicycle are safely in rotational equilibrium.
Bicycle
Rockets and Space Travel
Despite the complexity of modern spacecraft, the rocket is one of the simplest of all machines. It’s based on the principle that every action has a reaction. A rocket is propelled forward by pushing material out of its tail. As simple as rockets are, however, people have been developing better rockets for over 700 years. They’re used for such pursuits as space exploration, weaponry, rescue operations, and amusement.
Rocket Propulsion
Among a rocket’s most impressive features are its ability to propel itself forward even in the complete isolation of space and its capacity to reach astonishing speeds using that propulsion. It somehow manages to push itself forward without any outside help and to use that forward push to accelerate seemingly without limits. Of course, a rocket can’t really push itself forward, any more than you can lift yourself up by your boots, and it can’t accelerate forever. In reality, it obtains a forward force, a thrust force, by pushing against its own limited store of fuel, and when that fuel runs out, it stops accelerating.
At room temperature, the molecules in air are traveling about 1800 km/h (1100 mph). When gas molecules are heated to roughly 2800 ºC (5000 ºF), as they are in a liquid-fuel rocket engine, they move about three times that fast. If you throw something in one direction at that kind of speed, you receive quite a lot of momentum in the other direction.
That’s what a conventional rocket engine does. It uses a chemical reaction to create very hot exhaust gas from fuels contained entirely within the rocket itself. What started as chemical potential energy in those fuels becomes thermal energy during the reaction and then mostly directed kinetic energy as the hot gas rushes out of the rocket engine in a plume of incandescent exhaust.

The rocket engine exerts a tremendous backward force on the gas, accelerating that gas to exhaust velocities measured in kilometers per second or miles per second. The gas pushes forward equally hard on the rocket engine. Propelled by such rocket engines, spacecraft can reach astonishing heights and speeds.
Achieving those amazing exhaust velocities requires carefully designed nozzles, the bell-shaped nozzles through which the exhaust flows. Each nozzle allows the rocket to obtain as much forward momentum as possible from its exhaust by directing that exhaust backward and accelerating it to the greatest possible speed. The nozzles allow gases to convert their various internal energies into kinetic energy and are ideally suited for directing and accelerating gases. In the case of rocket exhaust, the most effective nozzle shape is a converging-diverging one, called a de Laval nozzle after its Swedish inventor, Carl Gustaf de Laval.
Inside the rocket and before the de Laval nozzle, the hot exhaust gas is tightly packed and its pressure is enormous. Like the gas in a spray bottle, this exhaust gas accelerates rapidly through the nozzle toward the lower pressure environment outside. The narrowing throat of that nozzle aids its acceleration, up to a point. When the gas reaches the narrowest part of the nozzle, it’s traveling at the speed of sound and its characteristics begin to change dramatically. To coax the supersonic exhaust gas to accelerate still further, the nozzle stops narrowing and begins to widen. The tightly packed exhaust gas expands in volume as it flows through that widening bell and thereby prepares to enter the more open environment outside the nozzle.
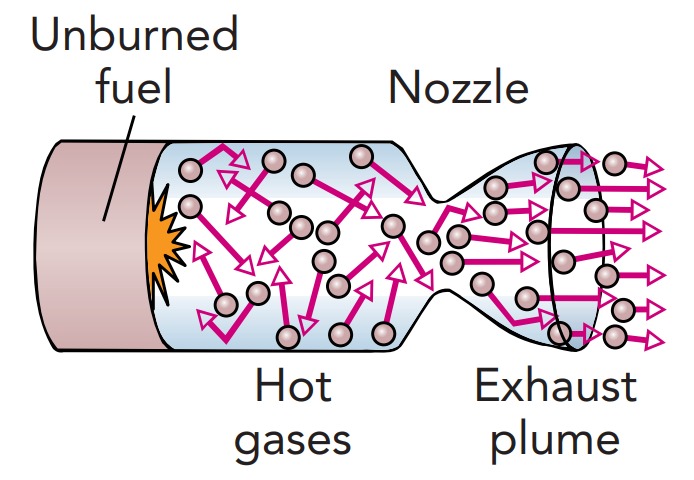
By the time the gas reaches the end of the de Laval nozzle, it has converted most of its original energy into kinetic energy, with its velocity directed away from the nozzle. In fact, because the gas actually continues to burn even as it flows through the nozzle, its kinetic energy and speed keep rising until they reach fantastic levels. With the help of the de Laval nozzle, exhaust gas leaves the rocket’s engine at an exhaust velocity, or backward-directed flow speed, of between 10,000 and 16,000 km/h (6000 and 10,000 mph).
As it creates this plume of exhaust, the rocket pushes the gas backward and gives it backward momentum. The gas completes the momentum transfer by pushing the rocket forward. The very act of ejecting the exhaust is all that’s required to obtain forward thrust; the rocket doesn’t need anything external to push and will operate perfectly well in empty space When it pushes hard enough on its exhaust, the rocket not only can support its own weight, it can even accelerate upward.
The Ultimate Speed of a Spacecraft
At rest on the launchpad, a rocket consists principally of a spacecraft and a supply of fuel. Once the rocket’s engine begins to fire, exhaust from the burned fuel accelerates backward and the spacecraft accelerates forward. The fuel is gradually consumed until eventually it runs out and the spacecraft coasts along on its own. For the spacecraft to reach speeds in excess of its exhaust speed, however, the rocket must push the majority of its initial mass backward as exhaust.
Unfortunately, that simple analysis overestimates the spacecraft’s speed. Because the rocket accelerates forward while its engine is firing, only the first portion of its exhaust travels backward at the full exhaust speed. As the rocket picks up speed in the forward direction, its exhaust moves less rapidly in the backward direction. When the rocket’s forward speed exceeds its exhaust speed, the exhaust actually ends up moving forward!
Despite this problem, a spacecraft can still travel forward faster than the exhaust speed; it just needs more fuel. If we neglect air resistance and weight, the spacecraft’s final speed is given by the rocket equation:
\[ spacecraft~ speed = exhaust~ speed · log_{e}\left( \frac{mass_{spacecraft} + mass_{fuel}}{mass_{spacecraft}} \right)\]
For a rocket that is 90% fuel and 10% spacecraft at launch, its spacecraft can reach 2.3 times the speed of its exhaust gas. If it is more than 90% fuel, it can go even faster.
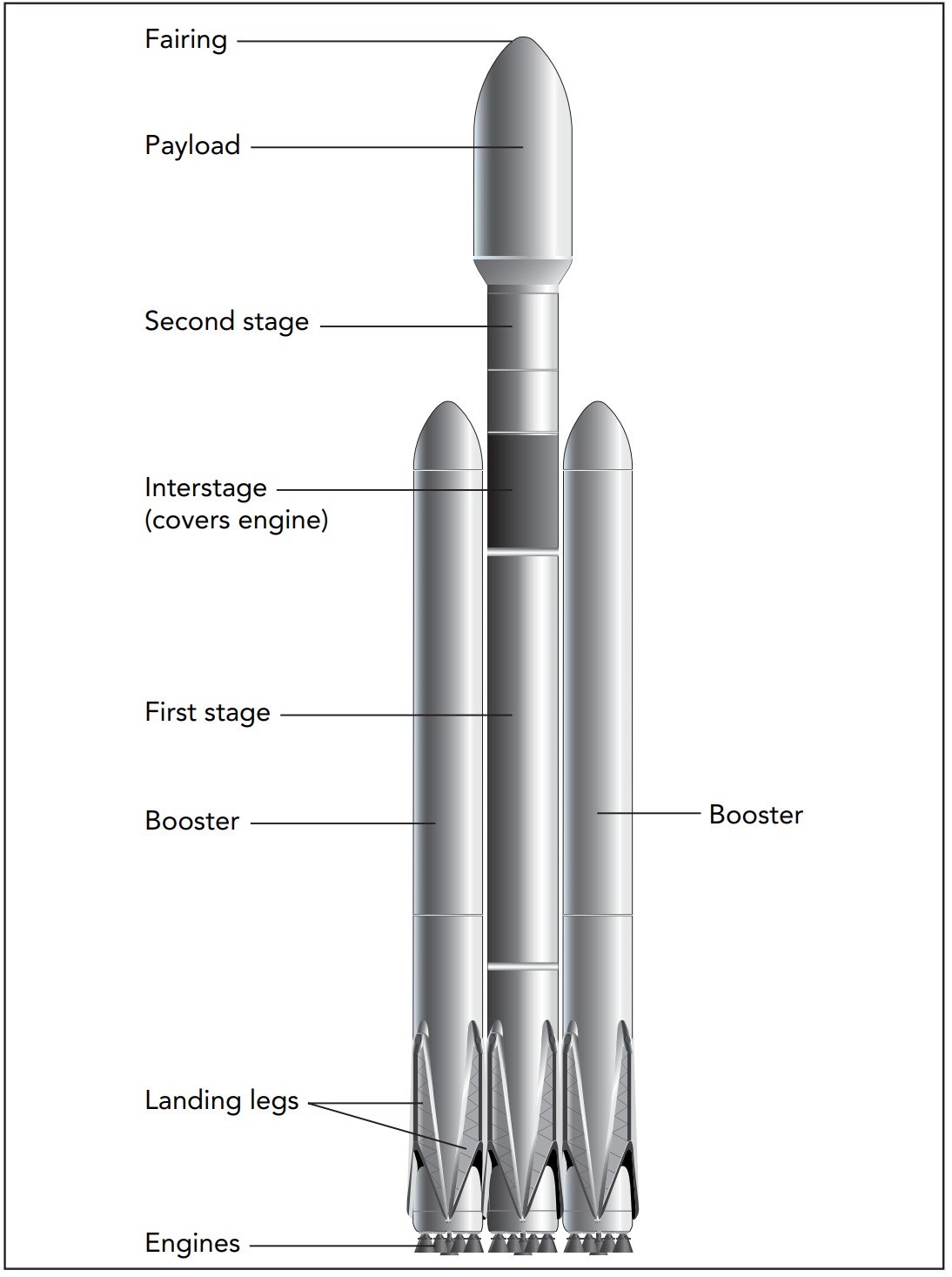
A space-bound rocket is typically a stack of several separate rocket stages, each stage much smaller than the previous stage. Once the first stage has used up all its fuel, the whole stage is discarded and the next rocket stage begins to operate. In this manner, the rocket behaves as though it’s ejecting almost all its mass as rocket exhaust. With the help of several stages and lots of fuel, rockets can travel substantially faster than their exhaust velocities and reach Earth orbit or the solar system beyond.
Rockets
Orbiting Earth
If the spacecraft were heading straight up when it ran out of fuel, it would either fall back to the ground or leave Earth forever (more on that later). But if it were heading primarily horizontally when its engine turned off, it might find itself circling Earth endlessly. With no atmosphere to affect it, the spacecraft follows a path determined only by inertia and gravity, and since the spacecraft’s weight causes it to accelerate toward the center of Earth, its trajectory can bend into a huge elliptical loop around Earth.
The spacecraft is following an orbit around Earth. An orbit is the path an object takes as it falls freely around a celestial object. Although the spacecraft accelerates directly toward Earth’s center at every moment, its huge horizontal speed prevents it from actually hitting Earth’s surface. Instead, Earth’s curved surface bends away from it so rapidly that the fast-moving spacecraft falls around Earth rather than into it . To orbit Earth just above the atmosphere, a spacecraft must travel at the enormous horizontal speed of 7.9 km/s (about 17,800 mph) and will circle Earth once every 84 minutes.
The farther the spacecraft’s orbit is from Earth’s surface, however, the longer its orbital period, the time it takes to complete one orbit. That longer period is due in part to the increased distance the spacecraft must travel when completing a larger orbit, but it’s also due to an important characteristic of gravity: Earth’s gravity becomes weaker as distance from Earth’s center of mass increases.
An object’s weight is equal to its mass times 9.8 N/kg, the acceleration due to gravity. That relationship, however, is only an approximation, valid for an object near Earth’s surface. As the object’s altitude increases, both the acceleration due to gravity and the object’s weight decrease—you truly weigh less on a mountaintop than you do in the valley nearby
To determine orbits around Earth and other celestial bodies, scientists and engineers use a more general formula that relates the gravitational forces between two objects to their masses and the distance separating them. These forces are equal to the gravitational constant times the product of the two masses, divided by the square of the distance separating them. This relationship, discovered by Newton and called the law of universal gravitation, can be written as a word equation:
\[ force = gravitational~ constant \frac {mass_{1} ~ mass_{2}}{(distance ~between~ masses)^{2}}\]
in symbols:
\[F = G \frac{m_{1}m_{2}}{r^{2}}\]
and in common language:
The pull of gravity is strongest between massive objects but diminishes rapidly as distance increases
The force on \(mass_{1}\) is directed toward \(mass_{2}\) and the force on \(mass_{2}\) is directed toward \(mass_{1}\). Those two forces are equal in magnitude but oppositely directed. The gravitational constant is a fundamental constant of nature, with a measured value of \(6.6720\) \(\times 10^{−11}\) \(Nm^{2}/kg^{2}\)
THE LAW OF UNIVERSAL GRAVITATION
Every object in the universe attracts every other object in the universe with a force equal to the gravitational constant times the product of the two masses, divided by the square of the distance separating the two objects
For a spacecraft orbiting Earth just above its atmosphere, that distance is roughly Earth’s radius of 6378 km (3964 miles). For a spacecraft far above the atmosphere, however, the distance is larger and the force of gravity is weaker; that spacecraft experiences a smaller acceleration due to gravity. To give it the additional time it needs for its path to bend around in a circle, the high-altitude spacecraft must travel more slowly than the low-altitude spacecraft. This reduced speed explains the long orbital periods of highaltitude spacecraft.
At 35,900 km (22,300 miles) above Earth’s surface, the orbital period reaches 24 hours. A satellite traveling eastward in such an orbit turns with the Earth and is said to be geosynchronous. If a geosynchronous satellite orbits Earth around the equator, it’s also geostationary—it always remains over the same spot on Earth’s equator. Such a fixed orientation is useful for communications and weather satellites.
Not all orbits are circular. The orbits of some spacecraft are elliptical, so their altitudes vary up and down once per orbit. At apogee, its greatest distance from Earth’s center, a spacecraft travels relatively slowly because it has converted some of its kinetic energy into gravitational potential energy. At perigee, its smallest distance from Earth’s center, the spacecraft travels relatively rapidly because it has converted some of its gravitational potential energy into kinetic energy.
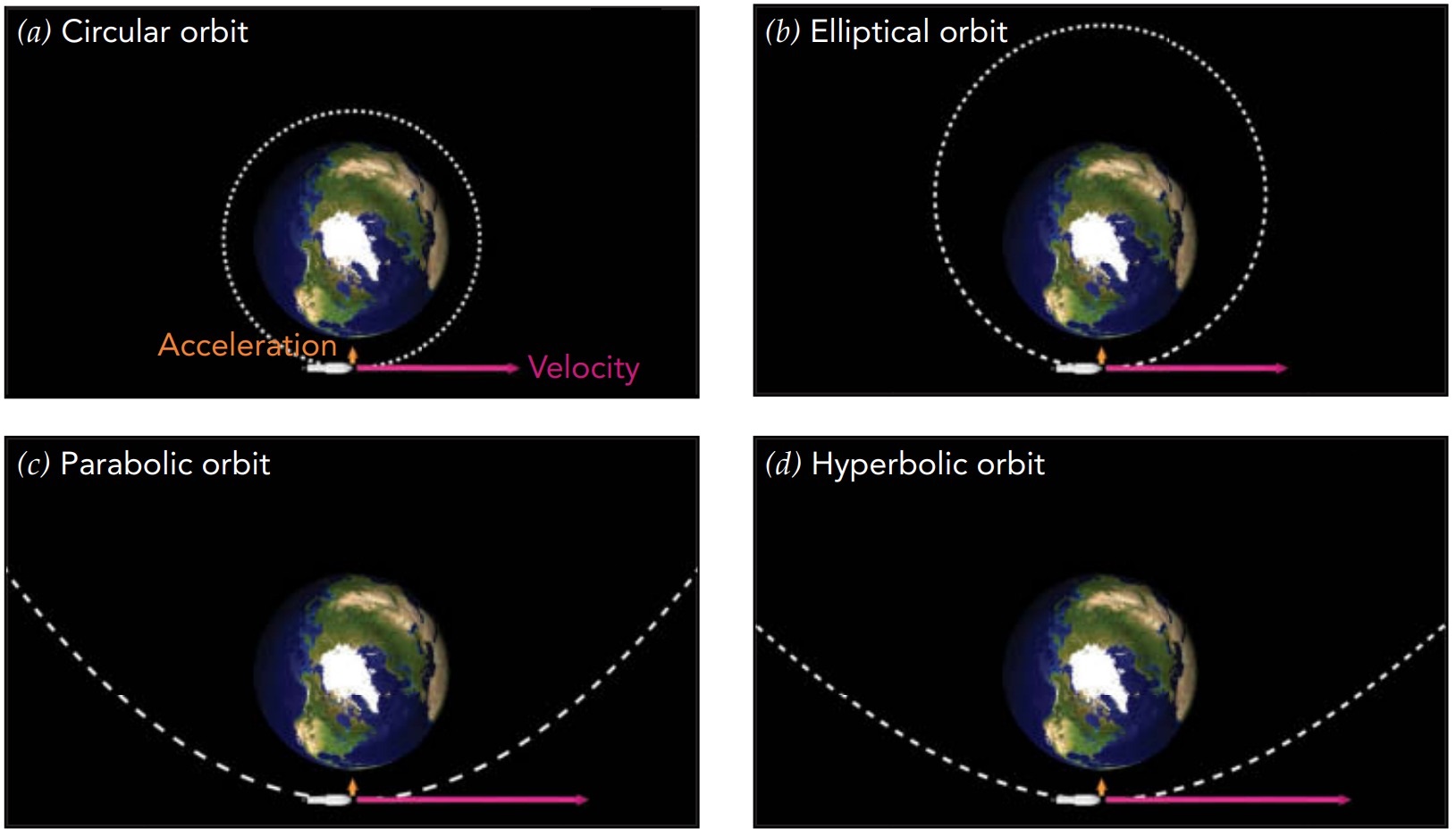
The greater a spacecraft’s total energy, the farther its orbit extends from Earth. If the spacecraft has too much total energy, Earth’s gravity will be unable to bend its path into a closed loop and the spacecraft will coast off into interplanetary space. The spacecraft’s path near Earth is then a parabola or hyperbola. The spacecraft follows this parabolic or hyperbolic path only once and then drifts away from Earth forever.
A spacecraft usually enters parabolic or hyperbolic orbit by firing its rocket engine. It starts in an elliptical orbit around Earth and uses its rocket engine to increase its kinetic energy. The spacecraft then arcs away from Earth, and its kinetic energy gradually transforms into gravitational potential energy. But Earth’s gravity becomes weaker with distance, and the spacecraft’s gravitational potential energy slowly approaches a maximum value even as its distance from Earth becomes infinite. If the spacecraft has enough kinetic energy to reach this maximum gravitational potential energy, it will be able to escape completely from Earth’s gravity. If its kinetic energy approaches zero as it escapes, it’s in a parabolic orbit. If it retains excess kinetic energy after the escape, it’s in a hyperbolic orbit.
The speed that a spacecraft needs to escape from Earth’s gravity is called the escape velocity. This escape velocity depends on the spacecraft’s altitude and is about 11.2 km/s (25,000 mph) near Earth’s surface. A spacecraft traveling at more than the escape velocity follows a hyperbolic orbital path and heads off toward the other planets or beyond.
Orbiting the Sun: Kepler’s Laws
Once it escapes from Earth’s gravity and again turns off its rocket engine, the spacecraft behaves like a tiny planet and orbits the sun. If you watch it patiently as it travels and compare its orbital motion with the motions of the planets themselves, you may begin to notice three universal features of all these solar orbits. First recognized by German astronomer Johannes Kepler (1571–1630) through his careful analysis of the extensive observational data collected by Danish astronomer Tycho Brahe, those three orbital behaviors are known as Kepler’s laws.
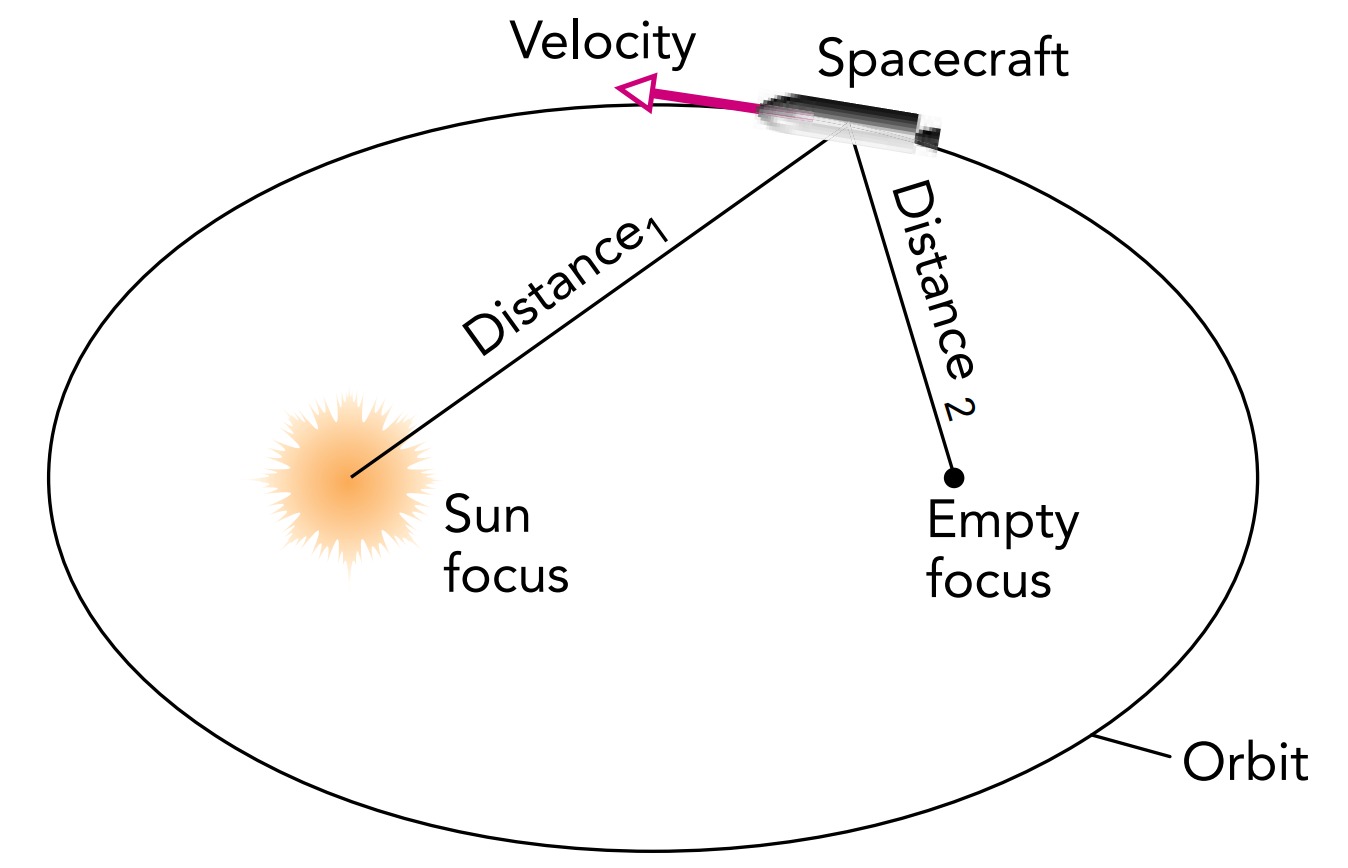
This law describes the shape of the spacecraft’s looping orbit around the sun; it’s an ellipse, with the sun at one focus of that ellipse. An ellipse isn’t an arbitrary oval; it’s a planar curve with two foci and a rule stating that the sums of the distances between each point on the curve and the two foci are the same. In this case, one focus is occupied by the sun, and the other focus is usually empty. If you add the distance from the spacecraft to the sun and the distance from the spacecraft to the empty focus, that sum will remain constant as the spacecraft orbits the sun. A circular orbit around the sun is a particularly simple elliptical one; its two foci coincide and the sun occupies them both.
KEPLER’S FIRST LAW: ORBITS
All planets move in elliptical orbits, with the sun at one focus of the ellipse
Kepler’s second law describes the area swept out by a line stretching from the sun to the spacecraft: that line sweeps out equal areas in equal times. Regardless of how circular or elongated the spacecraft’s orbit is, or where the spacecraft is along that orbit, the area marked off each second by that moving line is always the same.
This observation demonstrates another physical law—conservation of angular momentum. Since the sun’s gravity pulls the spacecraft directly toward the sun, it exerts no torque on the spacecraft and the spacecraft’s angular momentum about the sun is constant. Remarkably, the rate at which this line sweeps out area is proportional to the spacecraft’s angular momentum, so the steadiness of that sweep demonstrates the constancy of the spacecraft’s angular momentum about the sun
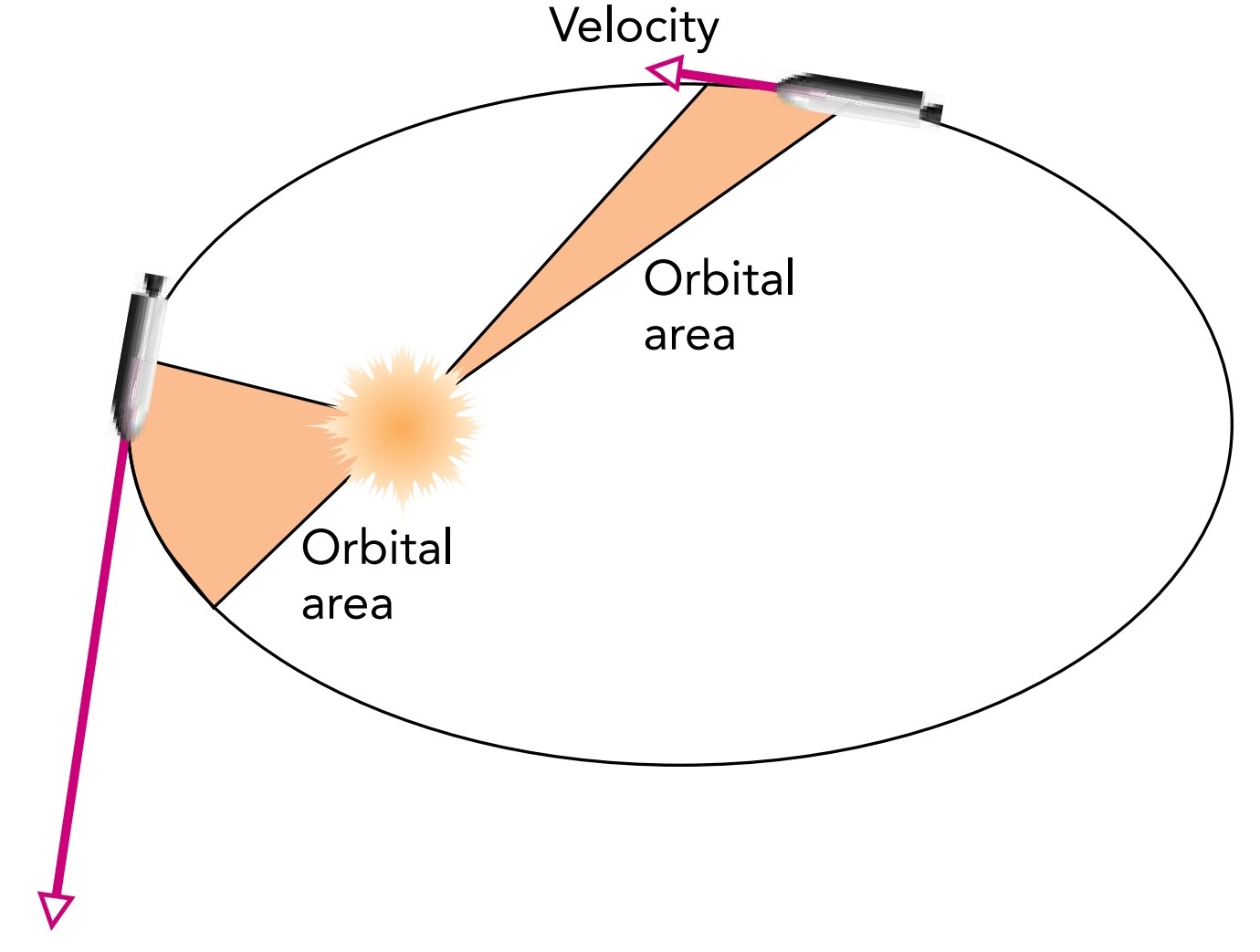
KEPLER’S SECOND LAW: AREAS
A line stretching from the sun to a planet sweeps out equal areas in equal times
Kepler’s third law describes the spacecraft’s orbital period around the sun: the square of its orbital period is proportional to the cube of its mean distance from the sun, that is, the average of its maximal and minimal distances from the sun. This relationship can be derived from the law of universal gravitation, the equations describing centripetal acceleration, and Newton’s second law.
KEPLER’S THIRD LAW: PERIODS
The square of a planet’s orbital period is proportional to the cube of that planet’s mean distance from the sun.

Travel to the Stars: Special Relativity
Despite formidable challenges, it may one day be possible for human-crewed spacecraft to venture away from the solar system and travel to the stars. The distances involved are so vast that the only way to cover them in an astronaut’s lifetime would be to move at fantastic speeds, speeds comparable to that of light itself.
Should spacecraft one day be able to attain such enormous speeds, they’ll find that the basic laws of motion, the Galilean and Newtonian laws that we have been learning up to this point, are incomplete. Although extremely accurate at ordinary speeds, those laws falter near the speed of light (exactly 299,792,458 m/s). They turn out to be low-speed approximations for the more accurate laws of motion developed by Einstein in 1905.
Built on the observation that light always travels at the same speed, regardless of an observer’s inertial frame of reference, these relativistic laws of motion are accurate at any speed. They are part of Einstein’s special theory of relativity, the conceptual framework that describes space, time, and motion in the absence of gravity. Special relativity recognizes that those observers can also disagree on the distance and time separating two events.

Special relativity has many consequences for high-speed space travel, but we’ll concentrate on how relativity alters two familiar conserved quantities: momentum and energy. At low speeds, our spacecraft’s momentum takes its usual Newtonian value: mass times velocity. But with increasing speed, a new relativistic factor enters the picture: \((1 − speed^{2}/light speed^{2})^{−1/2}\).
Relativistic momentum is equal to the object’s mass times its velocity times that factor. This relationship can be written as a word equation:
\[ relativistic momentum = \frac{mass \times velocity} {\sqrt{1 − \frac{speed^{2}} {light ~speed^{2}}}}\]
in symbols:
\[p = \frac{m v}{\sqrt{1 − \frac{v^{2}}{c^{2}}}}\]
and in common language:
For a spacecraft to reach the speed of light, its momentum would have to be infinite
At ordinary speeds, the relativistic factor is so nearly equal to 1 that this relativistic relationship is beautifully approximated by the Newtonian one. However, as the spacecraft’s speed begins to approach that of light itself, the relativistic factor spoils the simple proportionality between momentum and velocity. Momentum then increases more rapidly than velocity. One result of this change is that it becomes impossible to reach the speed of light, let alone exceed it. Even if the spacecraft’s thrust increases its forward momentum at a steady rate, its speed will increase less and less quickly. It will approach—but never reach—the speed of light
A similar change happens to the spacecraft’s energy as it approaches the speed of light. At low speeds, our isolated spacecraft’s kinetic energy takes its usual Newtonian value: Half its mass times the square of its speed. At high speeds, however, we must begin using relativistic energy. Relativistic energy is equal to the object’s mass times the square of the speed of light times the relativistic factor. This relationship can be written as a word equation:
\[relativistic~ energy = \frac{mass \times light~speed^{2}}{\sqrt{1 − \frac{speed^{2}} {light~ speed^{2}}}}\]
in symbols:
\[E = {m c^{2}}{\sqrt{1 − \frac{v^{2}}{c^{2}}}}\]
and in common language:
A spacecraft starts with a rest energy and its energy grows toward infinity as its speed approaches the speed of light
At ordinary speeds, the spacecraft’s relativistic energy can be approximated as:
\[relativistic energy = mass \times light ~speed^{2} + \frac{1}{2} ~ mass ~ speed^{2}\]
The usual Newtonian kinetic energy appears at the right in this approximation, but to its left is a new energy that we’ve never seen before. Called the rest energy, it’s present even when the spacecraft is motionless. Because the rest energy is constant, it doesn’t affect low-speed motion and was overlooked in the Newtonian laws. The relativistic version of energy has two implications for our spacecraft. First, the spacecraft’s energy increases so quickly as it nears the speed of light that it can never reach that speed. Second, the spacecraft’s initial store of energy before launch is associated with its initial mass.
Visiting the Stars: General Relativity
In its travels near stars and other massive celestial objects, our spacecraft is likely to encounter another surprise: the Newtonian view of gravity is also an approximation! Near extremely dense, massive objects, gravity is no longer accurately described by Newton’s law of universal gravitation. Instead, understanding gravity requires a new conceptual framework that Einstein first presented in 1916, the general theory of relativity.
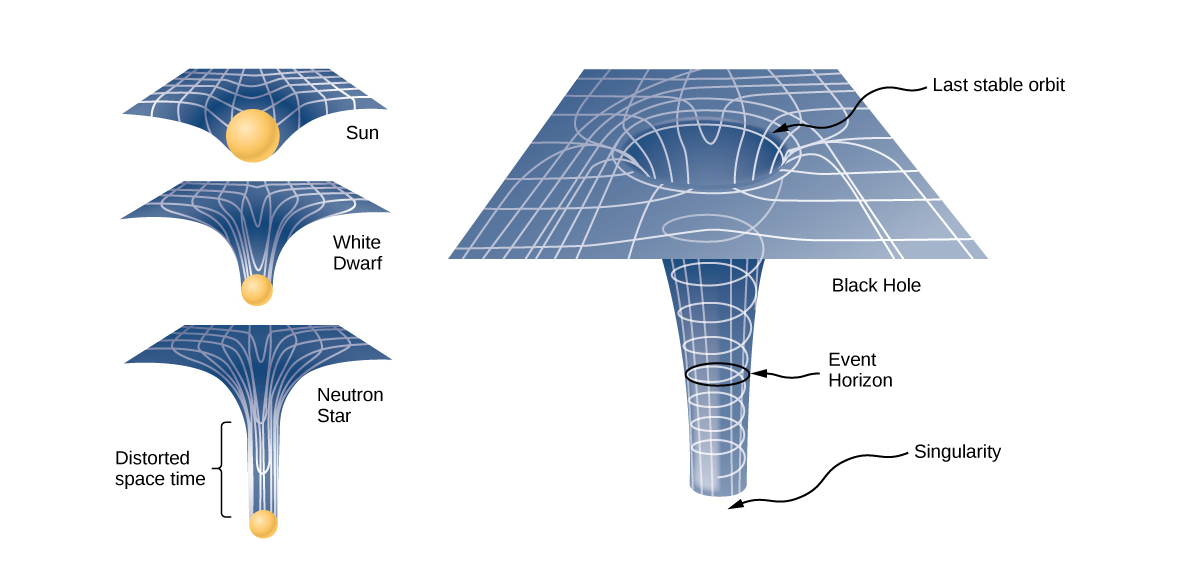
This new framework is based on the observation that you can’t distinguish between downward gravity and upward acceleration. They feel exactly the same. For example, if you feel heavy as you stand inside a closed spacecraft, you can’t be sure whether you’re experiencing a weight due to downward gravity or a feeling of acceleration due to upward acceleration. In fact, the spacecraft’s scientific instruments can’t help you because they can’t distinguish the effects of gravity from those of-acceleration either. No matter how hard you try, you can’t tell the difference.
We have seen mass play two apparently different roles that we can refer to as gravitational mass and inertial mass. When you’re experiencing a weight, your gravitational mass is acting together with gravity to make you feel heavy. When you’re experiencing a feeling of acceleration, your inertial mass is acting together with acceleration to make you feel heavy. an object that has a large inertial mass and is therefore difficult to shake back and forth also has a large gravitational mass and is therefore hard to support against gravity. In fact, the two masses seem to be the same. That observation led Einstein to propose the principle of equivalence, that these two masses, gravitational and inertial, are truly identical and therefore that no experiment you perform inside your spacecraft can distinguish between free fall and the absence of gravity. The general theory of relativity is based on this principle of equivalence.
As long as your spacecraft stays in regions of weak gravity, Newton’s law of universal gravitation will adequately describe its motion. At the extremes of gravity, however, the general theory of relativity is necessary. That theory describes a universe in which massive objects distort the structure of nearby space and time, and in which extreme masses produce extreme distortions. One of the most startling predictions of this theory is the existence of objects so radical in their gravitational warping of nearby space and time that they are black holes, spherical or nearly spherical surfaces from which not even light can escape. A number of black holes have been discovered, including an enormous one at the center of our galaxy. You might want to avoid them.