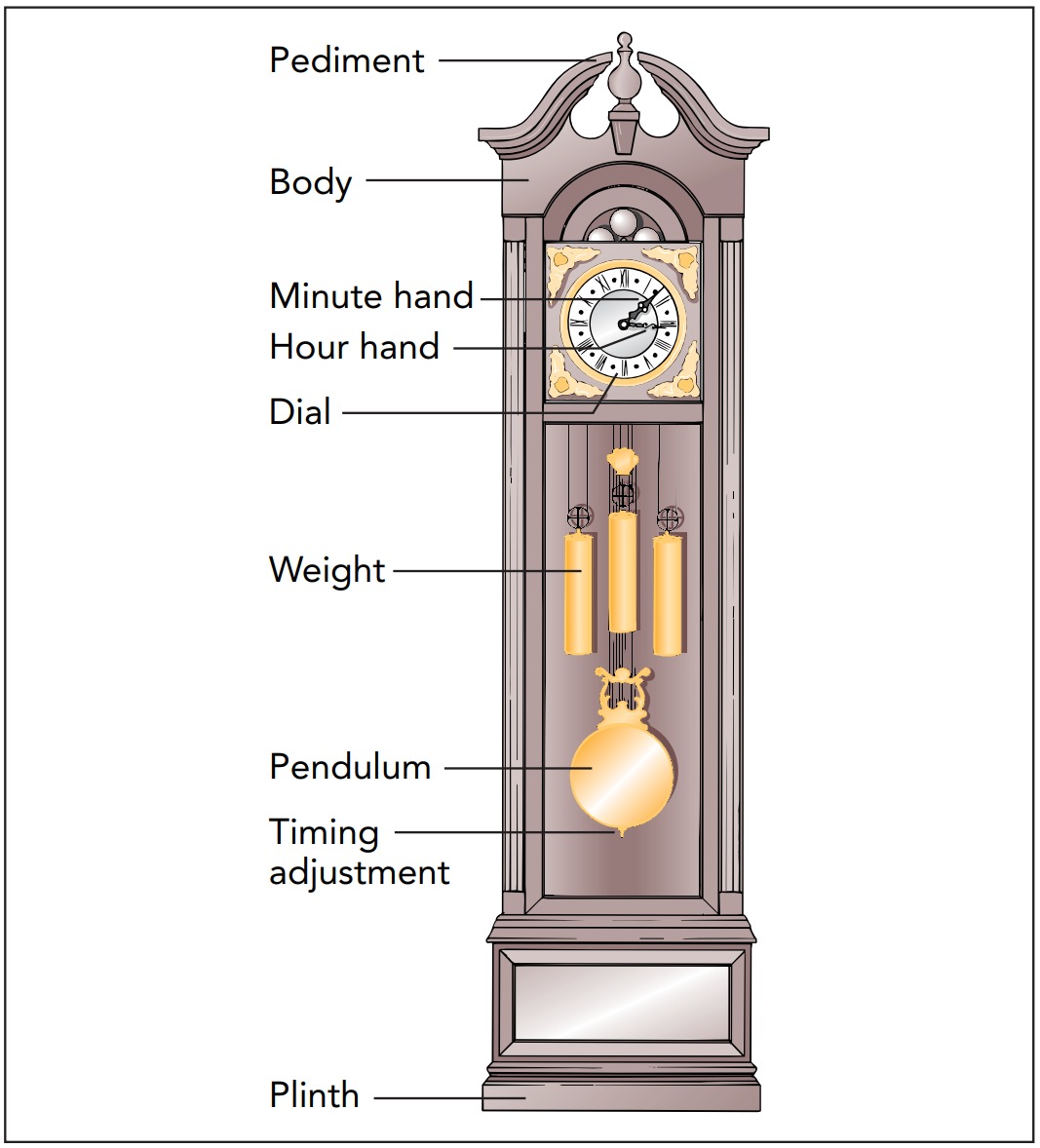
Introduction
Our lives are filled with cycles, from the sun’s daily passage overhead to a pond’s undulating ripples on a rainy day. These cyclic motions are governed by the physical laws and steadily mark our journey through time and space. Some of these cycles structure our lives out of necessity or tradition, while others are simply there to be observed. Still other cycles have become part of our everyday world because they’re useful or enjoyable. In this chapter, we cover those three possibilities by examining cyclic motions in three contexts: in clocks, in musical instruments, and at the seashore.
The wineglass’s vibration is an example of a natural resonance, a cyclic motion of the glass itself. Whether you tap the glass gently with a spoon or rub it with your finger, you’re causing it to undergo this characteristic motion.
Clocks
People measure their lives according to the sky, dividing existence into days, months, and years according to the celestial motions of the sun, moon, and stars. On the less romantic scale of daily life, the sky offers little help. Since it provides no easy way to measure short periods of time, people invented clocks. Early clocks were based on the time it took to complete simple processes—the flow of sand or water, or the burning of candles. However, these clocks had limited accuracy and required constant attention. Better clocks measure time with repetitive motions such as swinging or rocking. In this section, we’ll examine the workings of modern clocks based on repetitive motions.
Natural Resonances
An ideal timekeeping motion should offer both accuracy and convenience. The sun, moon, and stars keep excellent time but fail the Sure, conservation of energy, momentum, and angular momentum so convenience test dominate their motions that these celestial bodies move steadily and predictably through the heavens, century after century, but what do you do on a cloudy day? And while simple interval timers like sandglasses and burning candles are easy to make and use, they’re not very accurate. Besides, who’s going to stay up all night lighting fresh candles just to keep the “clock” running?
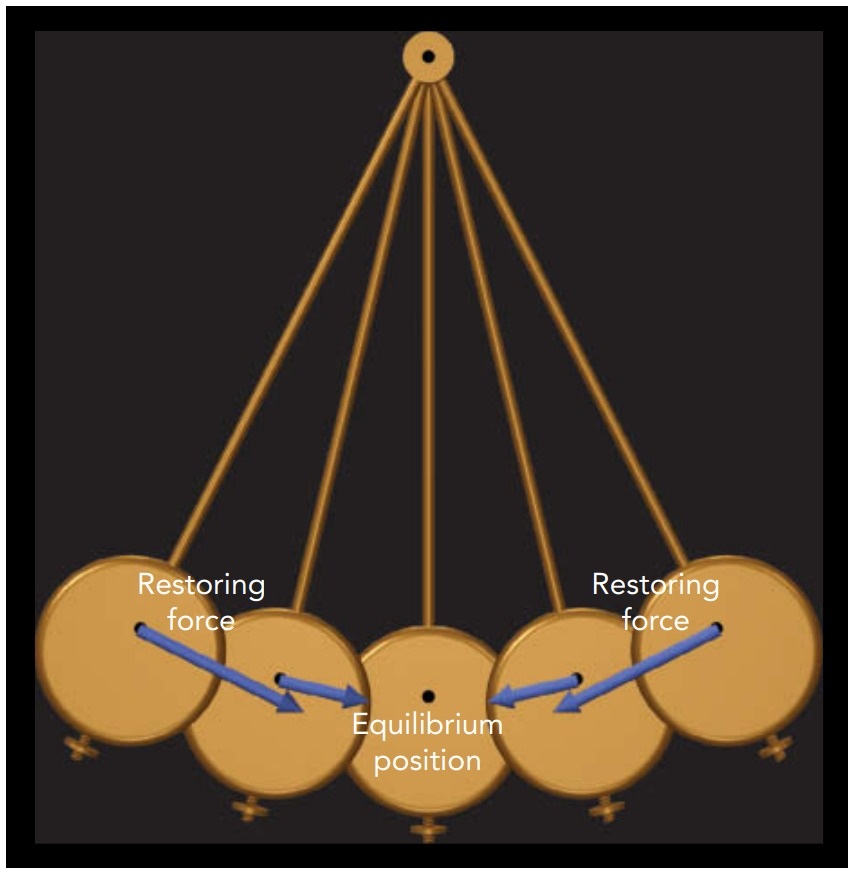
Practical clocks are based on a particular type of repetitive motion called a natural resonance. In a natural resonance, the energy in an isolated object or system of objects causes it to perform a certain motion over and over again. Many objects in our world exhibit natural resonances, from tipping rocking chairs to sloshing basins of water to waving flagpoles, and those natural resonances usually involve motion about a stable equilibrium. An object that has been displaced from its stable equilibrium accelerates toward that equilibrium but then overshoots; it coasts right through equilibrium and must turn around to try again. As long as it has excess energy, this object continues to glide back and forth through its equilibrium and thus exhibits a natural resonance
Pendulums and Harmonic Oscillators
One of the first natural resonances to find its way into clocks is the swing of a pendulum, a weight hanging from a pivot. When the pendulum’s center of gravity is directly below its pivot, it’s in a stable equilibrium. Its center of gravity is then as low as possible, so displacing it raises its gravitational potential energy and a restoring force begins pushing it back toward that equilibrium position.
For geometrical reasons, this restoring force is almost exactly proportional to how far the pendulum is from equilibrium. As you displace the pendulum steadily from equilibrium, the restoring force on it also increases steadily. When you release the displaced pendulum, its restoring force accelerates it back toward equilibrium. Instead of stopping, however, the pendulum swings back and forth about its equilibrium position in a repetitive motion called an oscillation. As it swings, its energy alternates between potential and kinetic forms. When it swings rapidly through its equilibrium position in the middle of a swing, its energy is all kinetic. When it stops momentarily at the end of a swing, its energy is all gravitational potential. This repetitive transformation of excess energy from one form to another is part of any oscillation and keeps the oscillator—the system experiencing the oscillation—moving back and forth until that excess energy is either converted into thermal energy or transferred elsewhere.

The pendulum isn’t just any oscillator, though. Because its restoring force is proportional to its displacement from equilibrium, the pendulum is a harmonic oscillator—the simplest and best understood mechanical system in nature. As a harmonic oscillator, the pendulum undergoes simple harmonic motion, a regular and predictable oscillation that makes it a superb timekeeper.
The period of any harmonic oscillator, the time it takes to complete one full cycle of its motion, depends only on how stiffly its restoring force pushes it back and forth, and on how strongly its inertia resists the accelerations of that motion. Stiffness is the measure of how sharply the restoring force increases as the oscillator is displaced from equilibrium; stiff restoring forces are associated with firm or hard objects, while less stiff restoring forces are associated with soft objects. The stiffer the restoring force, the more forcefully it pushes the oscillator back and forth and the shorter the oscillator’s period. On the other hand, the larger the oscillator’s mass, the less it accelerates and the longer its period.
However, the most remarkable and important characteristic of a harmonic oscillator is not that its period depends on stiffness and mass, but that its period doesn’t depend on amplitude, its furthest displacement from equilibrium. Whether that amplitude is large or small, the harmonic oscillator’s period remains exactly the same. This insensitivity to amplitude is a consequence of its special restoring force, a restoring force that is proportional to its displacement from equilibrium. At larger amplitudes, the oscillator travels farther each cycle, but the forces accelerating it through that cycle are stronger as well. Overall, the harmonic oscillator completes a large cycle of motion just as quickly as it completes a small cycle of motion.
Any harmonic oscillator can be thought of as having a restoring force component that drives the back and forth motion and an inertial component that resists that motion. Their competition determines the oscillator’s period. Harmonic oscillators with stiff restoring forces and little inertia have short periods, while those with soft restoring forces and great inertia have long periods. Their amplitudes of oscillation simply don’t affect their periods, which is why harmonic oscillators are so ideal for timekeeping. Because practical clocks can’t control the amplitudes of their timekeeping oscillators perfectly, virtually all of them are based on harmonic oscillators.
A pendulum’s period does, however, depend on its length and on gravity. When you reduce the pendulum’s length, the distance from its pivot to its center of mass, you stiffen its restoring force and shorten its period. Similarly, when you strengthen gravity (perhaps by traveling to Jupiter), you increase the pendulum’s weight, stiffen its restoring force, and reduce its period. Though we won’t try to prove it, the period of a pendulum is
\[period ~of ~pendulum = 2\pi \sqrt{\frac{length~ of~ pendulum}{acceleration~ due ~to~ gravity}} \]
Thus a short pendulum swings more often than a long one, and any pendulum swings more often on Earth than it would on the moon.
On Earth’s surface, a 0.248 m pendulum has a period of 1 s, making it suitable for a wall clock that advances its second hand by 1 s each time the pendulum completes a cycle. Since a pendulum’s period increases as the square root of its length, a 0.992-m pendulum (four times as tall as a 0.248 m pendulum) takes 2 s to complete its cycle and is appropriate for a floor clock that advances its second hand by 2 s per cycle.
Because a pendulum’s period depends on its length and gravity, a change in either one causes trouble. A simple pendulum slows down as it heats up because materials expand with increasing temperature. A more accurate pendulum is thermally compensated by using several different materials with different coefficients of loudness expansion to ensure that its center of mass remains at a fixed distance from its pivot. Although gravity doesn’t change with time, it does vary slightly from place to place. To correct for differences in gravity between the factory and a clock’s final destination, its pendulum has a threaded adjustment knob. This knob allows you to change the pendulum’s length to fine-tune its period.
Pendulum Clocks
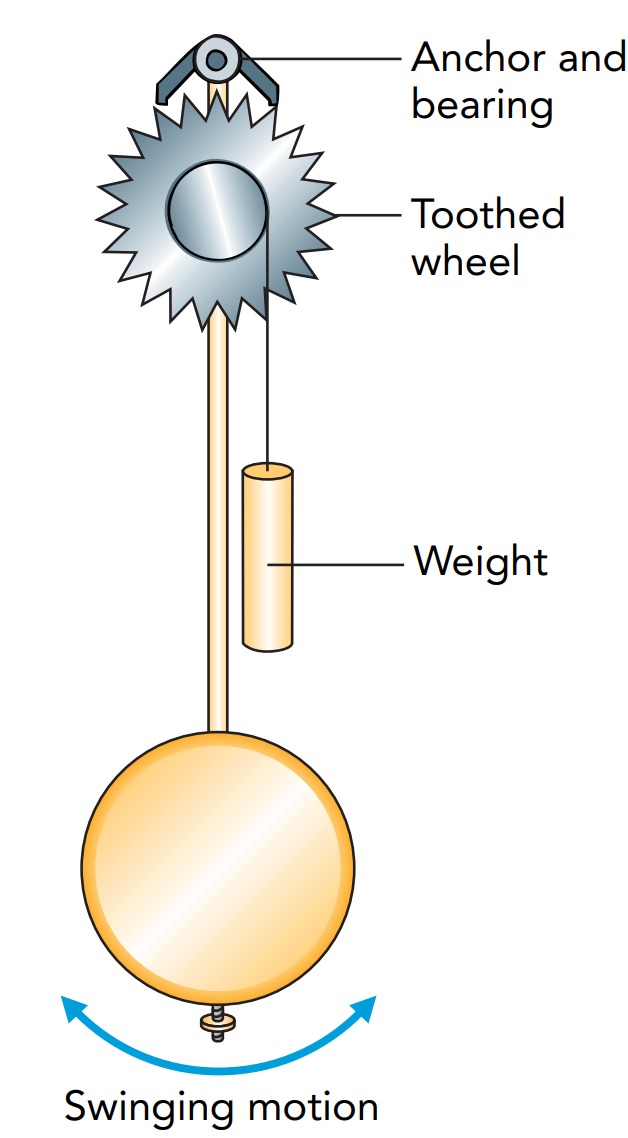
Although a pendulum maintains a steady beat, it’s not a complete clock. Something must keep the pendulum swinging and use that swing to determine the time. A pendulum clock does both. It sustains the pendulum’s motion with gentle pushes, and it uses that motion to advance its hands at a steady rate.
The toothed wheel also keeps the pendulum moving by giving the anchor a tiny forward push each time the pendulum completes a swing. Since the anchor moves in the direction of the push, the wheel does work on the anchor and pendulum, and replaces energy lost to friction and air resistance. This energy comes from the weighted cord, which releases gravitational potential energy as its weight descends. When you wind the clock, you rewind this cord around the shaft, lifting the weight and replenishing its potential energy. The most accurate timekeepers are those that can oscillate without any assistance or energy replacement for thousands or millions of cycles. These precision timekeepers need only the slightest pushes to keep them moving and thus have extremely precise periods.
Electronic Clocks
The potential accuracy of pendulum and balance clocks is limited by friction, air resistance, and thermal expansion to about 10 s per year. To do better, a clock’s timekeeper must avoid these mechanical shortcomings. Many modern clocks use quartz oscillators as their timekeepers.
A quartz oscillator is made from a single crystal of quartz, the same mineral found in most white sand. Like many hard and brittle objects, a quartz crystal oscillates strongly after being struck. Since their restoring forces are proportional to displacement from equilibrium, both systems are harmonic oscillators. Because of its exceptional hardness, a quartz crystal’s restoring forces are extremely stiff. Even a tiny distortion leads to huge restoring forces. Since the period of a harmonic oscillator decreases as its spring becomes stiffer, a typical quartz oscillator has an extremely short period. Its motion is usually called a vibration rather than an oscillation because vibration implies a fast oscillation in a mechanical system.


Because of its rapid vibration, a quartz oscillator’s period is a small fraction of a second. We normally characterize such a fast oscillator by its frequency, the number of cycles it completes in a certain amount of time. The SI unit of frequency is the cycle per second, also called the hertz (abbreviated Hz) after German physicist Heinrich Rudolph Hertz. Period and frequency are reciprocals of one another, frequency = 1 period , so an oscillator with a period of 0.001 s has a frequency of 1000 Hz. Because the vibrating crystal isn’t sliding across anything or moving quickly through the air, it loses energy slowly and vibrates for a long, long time. Also, because quartz’s coefficient of thermal expansion is extremely small, the crystal’s period is nearly indepen-dent of its temperature. With its exceptionally steady period, a quartz oscillator can serve as the timekeeper for a highly accurate clock, one that loses or gains less than a tenth of a second per year.
The quartz crystal in this wristwatch is located inside the silver cylinder at the bottom. Carefully polished to vibrate at a precise frequency, the crystal keeps the watch accurate to a few seconds a month.
Of course, a quartz crystal isn’t a complete clock. Like the pendulum and balance, it needs something to keep it vibrating and to use that vibration to determine the time. Because of this coupling between its mechanical and electrical behaviors, crystalline quartz is known as a piezoelectric material and is ideal for electronic clocks. The clock’s circuitry uses electrical stresses to keep the quartz crystal vibrating. Just as carefully timed pushes keep a child swinging endlessly on a playground swing, carefully timed electrical stresses keep the quartz crystal vibrating endlessly in its holder. Because the crystal loses so little energy with each vibration, only a tiny amount of work is required each cycle to maintain its vibration. The clock also detects the crystal’s vibrations electrically. Each time its halves move in or out, the crystal experiences mechanical stress and emits a pulse of electricity. These pulses may control an electric motor that advances clock hands or may serve as input to an electronic chip that measures time by counting the pulses.
Shaped like a tiny tuning fork, this watch crystal vibrates almost exactly 32,768 times per second. Burn marks at its tips were created when its vibrational frequency was tuned by a laser beam.
Clock
Sea Surfing
The sea is never still. If you’ve visited the seashore, you’ve probably noticed two of the sea’s most important motions: tides and surface waves.
The Tides
If you watch the sea for a few days, you’ll notice the tides. In a cycle as old as the oceans themselves, the water level rises for about 6¼ hours to reach high tide, drops for about 6¼ hours to arrive at low tide, and then begins rising again. The tides are caused by Earth’s rotation, the moon’s gravity, and, to a lesser extent, the sun’s gravity.
On Earth, the moon’s gravity is so weak that we normally don’t notice it. The moon is far away, and gravity diminishes with distance. But this dependence on distance also means that the moon’s gravity is stronger on one side of Earth than the other; you experience a stronger pull when you’re on the side of Earth nearest the moon than you do when you’re on the side opposite it. Although you can’t feel these variations in moon gravity yourself, Earth’s oceans respond to them. The oceans are deformed by the moon’s gravity , and this deformation produces the tides.
The differences between the moon’s gravity at particular locations on Earth and its average strength for the entire Earth give rise to tidal forces, residual gravitational forces that act to displace those locations relative to Earth as a whole. The near side of Earth is pulled toward the moon more strongly than average, so it experiences a tidal force toward the moon. The far side of Earth is pulled less strongly than average, so it experiences a tidal force away from the moon.
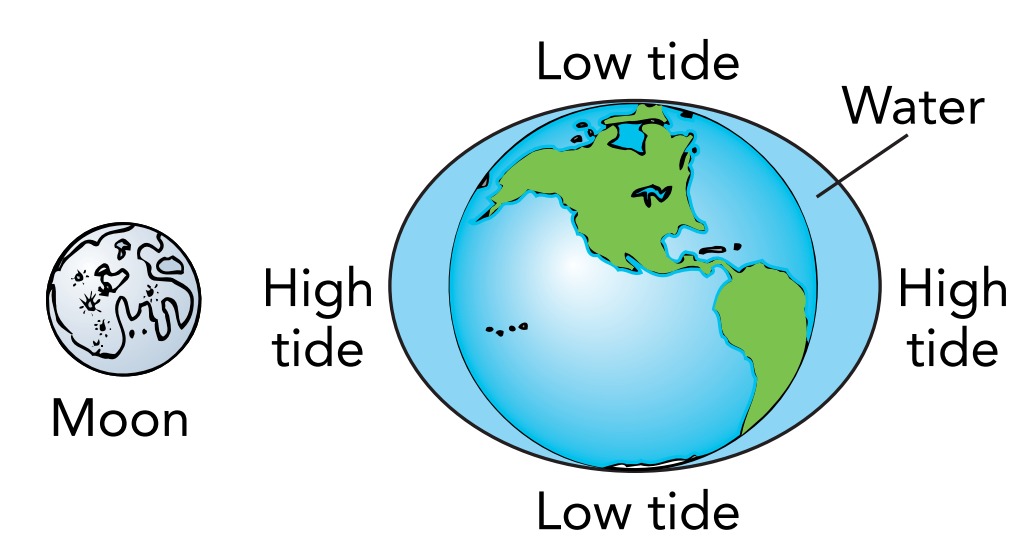
If Earth were less rigid, these tidal forces would stretch it into an egg shape. The near side of Earth would bulge outward toward the moon, while the far side of Earth would bulge outward away from the moon. But while Earth itself is too stiff to deform much, the oceans are not and they bulge outward in response to the tidal forces. Two tidal bulges appear: one closest to the moon and one farthest from the moon. The near-side bulge develops because the water there tries to fall toward the moon faster than Earth does as a whole. The far-side bulge forms because water there tries to fall toward the moon slower than Earth does as a whole. A beach located in one of these tidal bulges experiences high tide, while one in the ring of ocean between the bulges experiences low tide.
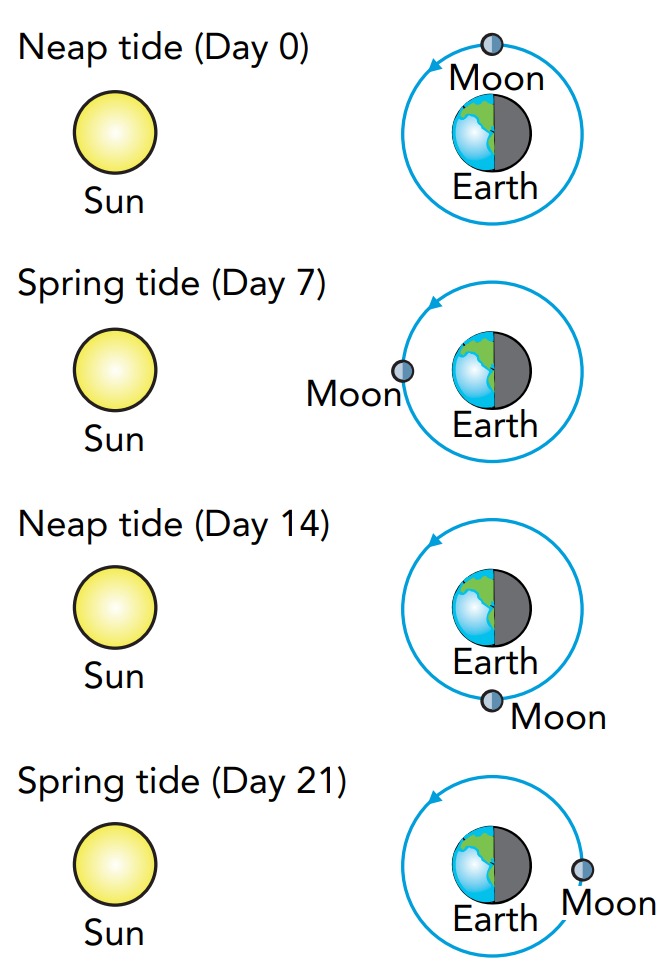
The moon isn’t the only source of tidal forces on Earth’s oceans. Although the sun is much farther away from Earth than the moon is, it’s so massive that the tidal forces it exerts are almost half as large as those exerted by the moon. The sun’s principal effect is to increase or decrease the strength of the tides caused by the moon. When the moon and the sun are aligned with one another, their tidal forces add together and produce extra large tidal bulges. When the moon and the sun are at right angles to one another, their tidal forces partially cancel and produce tidal bulges that are unusually small. Twice each lunar month, the tides are particularly strong. These spring tides occur whenever the moon and sun are aligned with one another (full moon and new moon). Twice each lunar month the tides are particularly weak. These neap tides occur whenever the moon and sun are at right angles to one another (half moon). The tides vary over a lunar month. They’re strongest when the sun and the moon are aligned (spring tides) and weakest when they are at 90° from one another (neap tides).
You can observe standing gravity waves on the surface of a large cup of coffee. As you walk with the cup in hand and jostle it back and forth rhythmically, you’ll produce gravity waves on the coffee’s surface. If you time your walking motion so that it’s synchronized with the natural rhythm of a particular standing wave, you’ll build up the amplitude of that wave by resonant energy transfer and may find yourself needing a change of clothes.
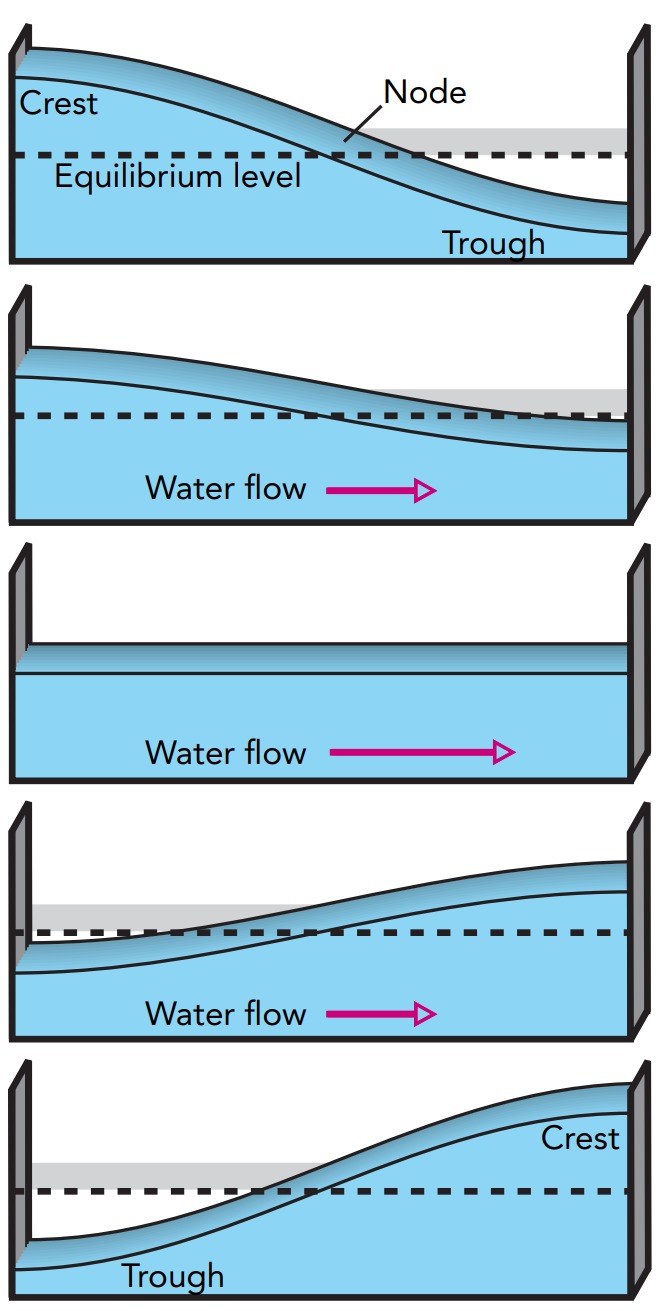
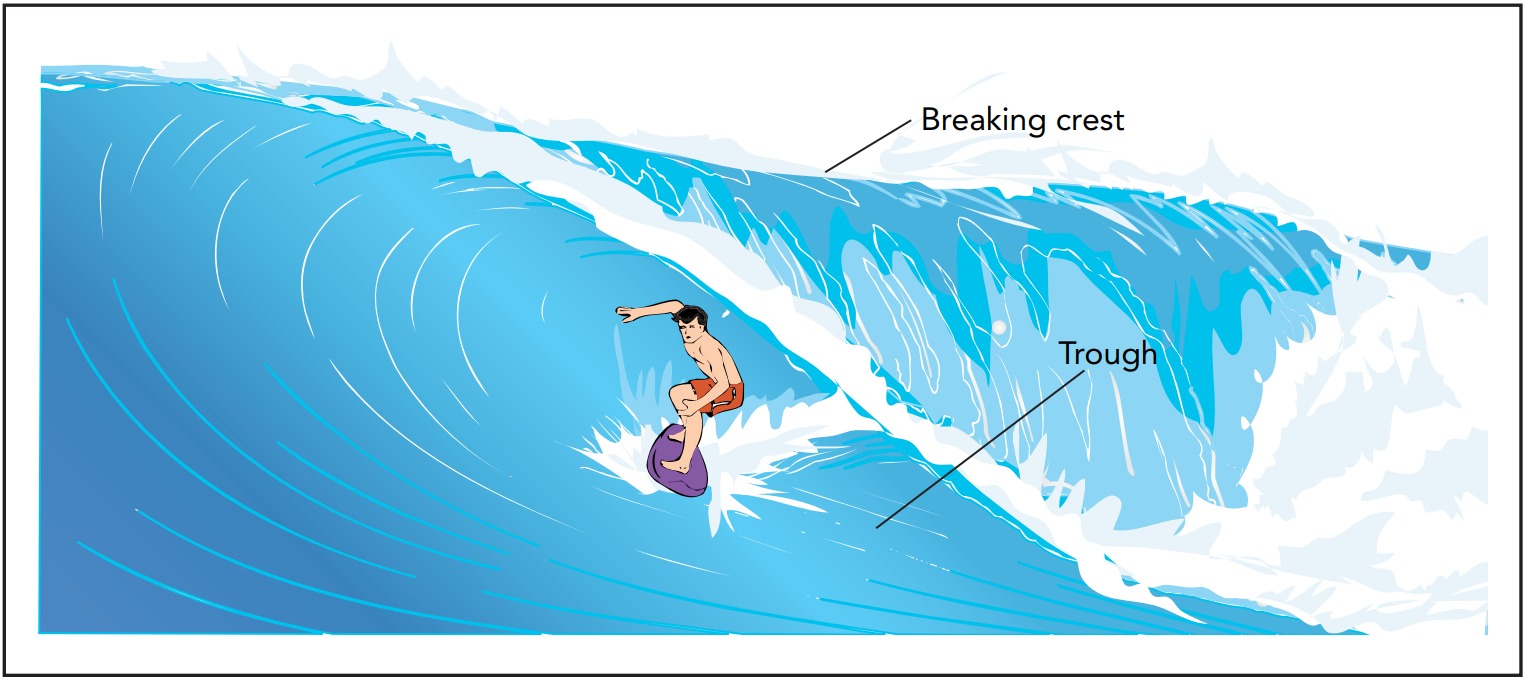
Standing surface waves on water are transverse—the water’s vertical surface vibrations are perpendicular to the horizontal waves themselves. In a basin, the fundamental vibrational mode has a node along the middle of the basin and antinodes at either end. At one antinode, water arcs up to a crest—a maximum upward displacement from equilibrium. At the other antinodes, water arcs down to a trough—a maximum downward displacement from equilibrium. Over time, the crest drops to become a trough, while the trough rises to become a crest. That process reverses and then repeats, over and over again until the sloshing water turns all its vibrational energy into thermal energy or transfers it elsewhere.
the basic modes of oscillation on a channel or lake are standing surface waves—the simplest waves on that limited surface. In a standing wave, the water’s surface oscillates up and down vertically, with its crests and troughs interchanging periodically: crests become troughs and troughs become crests. The standing wave’s pattern of crests and troughs doesn’t move anywhere; it simply flips up and down in place at a certain frequency.
Traveling Waves on the Surface of Water
As you sit at the seashore on a cloudless day, enjoying a warm, steady breeze, you can’t help but notice that the sea in front of you is covered with ridges. These ridges move steadily toward land and finally crash on the beach. Though it’s customary to think of each breaking swell as a separate wave, we’ll find it useful to view the entire moving pattern of evenly spaced ridges as a single wave—a traveling surface wave on water.
Traveling surface waves are the basic modes of oscillation on the open ocean, the simplest waves on that effectively limitless surface. Despite their steady progress across the water, these traveling waves actually involve oscillation. You can see this oscillation by watching a fixed point on the water’s surface. That point fluctuates up and down as the crests and troughs of a traveling wave pass through it. The period of this oscillation is the time required for one full cycle of rise and fall, and the frequency is the number of crests passing through that fixed point each second. Giant tides occur through resonant energy transfer when the cycle of the tides gradually builds up the amplitude of a suitable standing wave in a channel.
The ocean’s surface can host an incredible variety of traveling waves, each moving in its own direction with its own period and frequency. Moreover, these basic waves can coexist, adding together on the ocean’s surface to create ever more complicated patterns. When the ocean is rough and its surface features are ripples layered on swells layered on broad undulations, you’re seeing this superposition of “pure tone” traveling waves in all its glory
Both standing and traveling water surface waves carry energy—energy that they typically obtain from the wind, the tide, and occasionally seismic activity. Each wave’s energy consists of kinetic energy in moving water and gravitational potential energy in water that has been displaced from its level equilibrium. In a standing wave, the energy of the entire wave fluctuates back and forth between kinetic and gravitational potential; the wave’s kinetic energy peaks as the surface rushes through its level equilibrium, and its potential energy peaks as the surface stops to turn around at its maximum displacement from equilibrium. A traveling wave’s crests and troughs move steadily forward, so the water is never level or motionless. The energy in a traveling wave is therefore always an even mixture of kinetic and potential energies. Also, because of its directed motion, a traveling wave carries momentum pointing in the same direction as the wave velocity
The Structure of a Water Wave
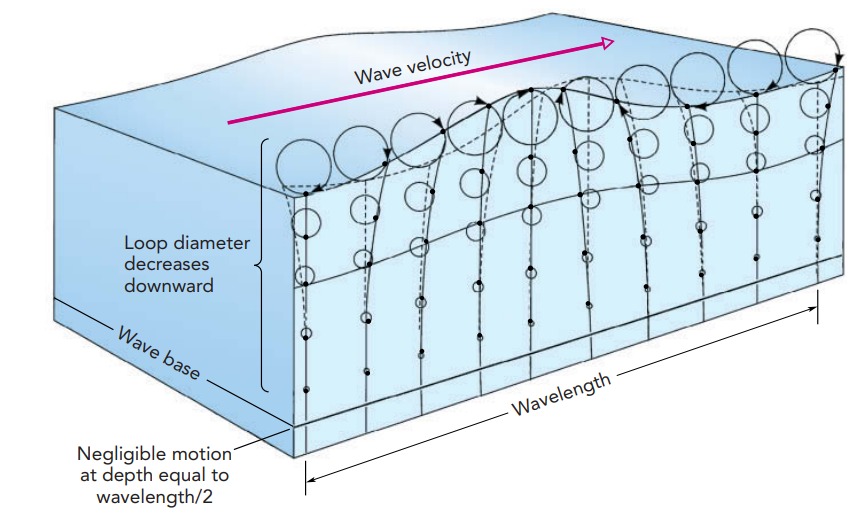
Let us watch a bottle floating on the water’s surface As a wave passes it. The bottle rises and falls with the crests and troughs, but it makes no overall progress in any direction. Instead, the bottle travels in a circle. Like the bottle, the water itself doesn’t actually move along with the passing wave. Although this water bunches up to create each crest and spreads out to create each trough, it returns to its starting point once the wave has left.

A patch of water on the ocean’s surface moves in a circular pattern as a traveling wave passes. Water that starts out on top of a crest moves down and forward as the crest departs. It moves down and backward as the trough arrives, then up and backward as the trough departs, and finally up and forward as the next crest arrives. When it reaches the top of the arriving crest, this water is back where it started on the ocean’s surface. The water at the top of a crest always moves in the same direction as the wave itself. water beneath the surface also circles. However, the circles diminish in radius gradually with depth and become negligible at a depth roughly equal to half the wave’s wavelength. Thus although it’s called a surface wave, it has a depth to it and therefore a sensitivity to shallow water.
These surface waves speed increases with wavelength. Such dependence of wave speed on wavelength is known as dispersion. It occurs in this case because water’s surface is surprisingly stiff when carrying long-wavelength waves. water’s surface uses its weight to oppose long-wavelength disturbances almost as vigorously as it opposes short-wavelength ones. That heightened stiffness for long-wavelength waves boosts their frequencies and therefore increases their wave speeds.
Little ripples have short wavelengths and travel slowly, while large ocean swells have long wavelengths and travel much more rapidly. Giant waves produced by earthquakes and volcanic eruptions, known as tsunamis, have extremely long wavelengths and can travel at hundreds of kilometers per hour. Because these giant waves travel so fast and move water so deep in the ocean, they carry enormous amounts of energy and momentum and are potentially disastrous to shore areas.
Waves at the Shore
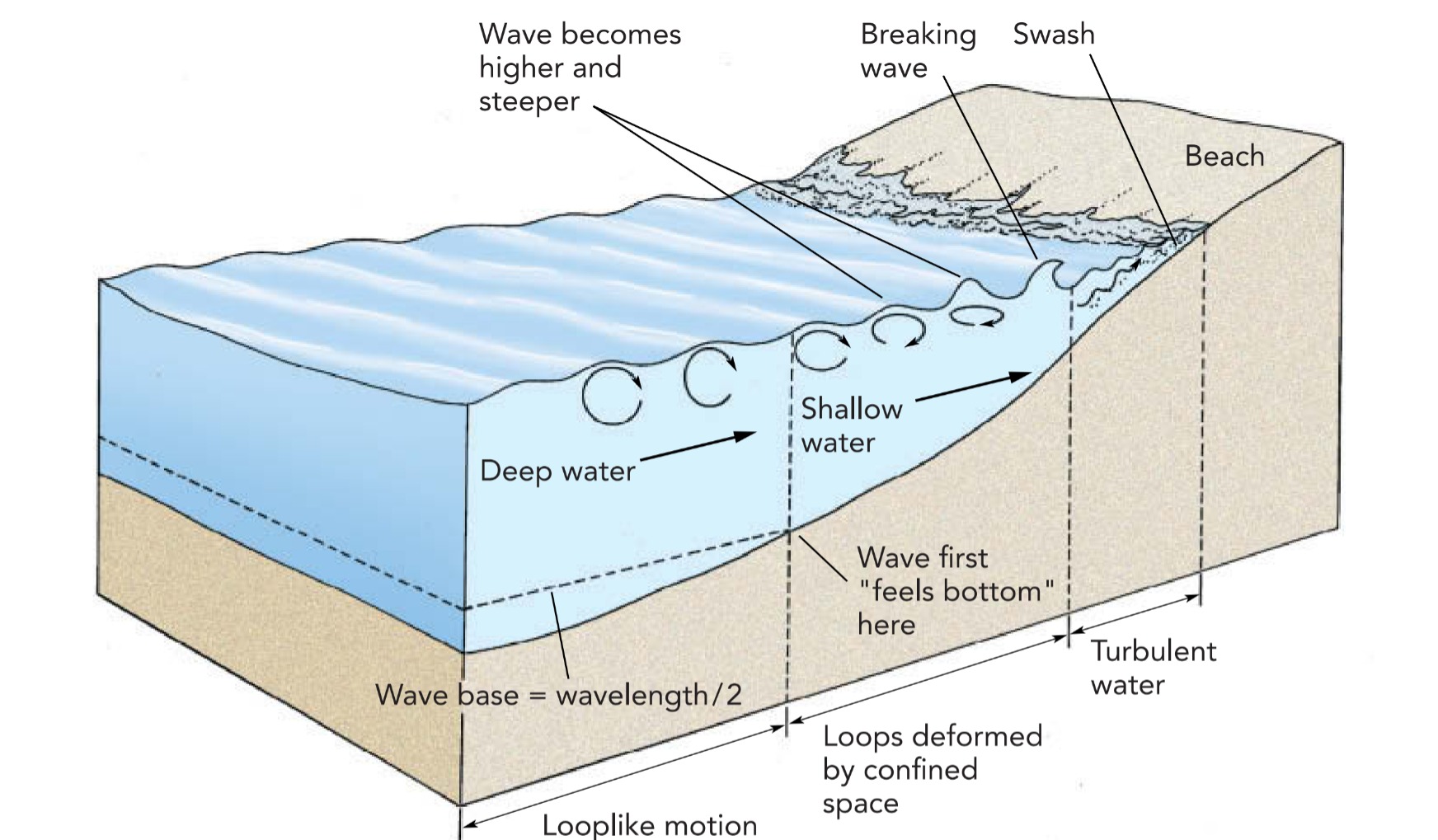
As a wave approaches the shore, it begins to travel through shallow water. Since the water’s circular motion extends below the surface, there comes a point at which the wave begins to encounter the seabed. Once the water is shallower than half the wavelength of the wave, the seabed distorts the water’s circular motion so that it becomes elliptical.
That change has a number of interesting effects on the wave. First, its wave speed gradually decreases so that the crests begin to bunch together. Second, its amplitude (the height of its crests and depth of its troughs) increases as the wave acts to keep its overall forward momentum constant despite its decrease in speed. These two effects explain why waves that look broad and gradual on the open ocean look quite steep and dangerous nearer the beach. Their crests have bunched together and grown taller, so the slopes between crests and troughs really have become steeper.
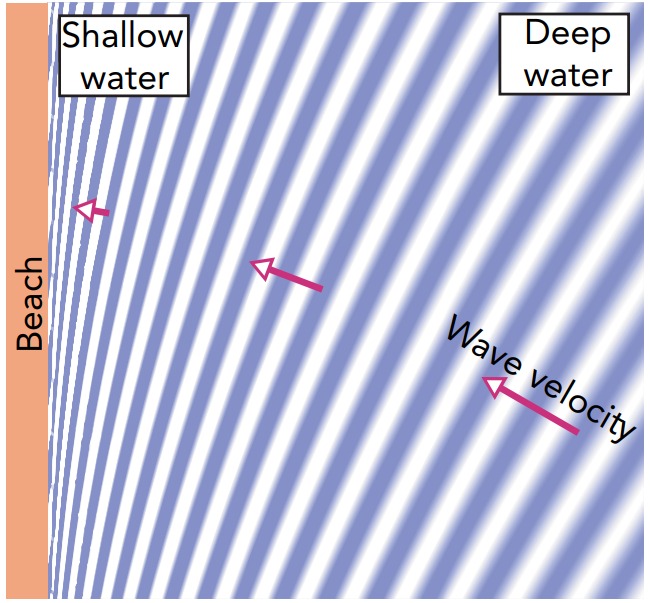
A third effect of the shallowing water is a gradual change in the wave’s direction of travel. Known as refraction, this bending occurs whenever a wave’s speed changes as it passes from one environment to another. Since a water surface wave slows as it approaches the shore, that wave refracts—it bends—so as to head more directly toward the shore. Because of refraction, waves approach the beach almost perpendicular to it, even if they were traveling at relatively oblique angles far from shore.
A fourth and final effect is the destruction of the wave—it eventually runs out of water and crashes onto the beach. The wave builds each of its crests using local water. When the crest enters very shallow water, there isn’t enough water in front of it to construct its forward side. The crest becomes incomplete and begins to “break.” The form of its demise depends on the slope of the seabed. If that slope is gradual, the wave breaks slowly to form a smooth, rolling, “boiling” surf. However, if the slope of the seabed is steep, the wave breaks quickly by having the top of its crest plunge forward over the trough in front of it. The steep slope essentially prevents the forward half of the crest from forming. The rearward half continues through its normal circular motion and dives over the missing half-crest in front of it.
Less severe changes in how a wave travels on opposite sides of a boundary can also make that wave reflect from the boundary, if only partially. Thus when a water surface wave passes over a sandbar or coral reef and its wave speed changes, it may experience both partial reflection and refraction. These effects contribute to the complicated dynamics of waves near the shore.
The Rhythm of the Surf: Wave Interference
If the ocean were carrying only one pure traveling wave toward shore, every breaking swell would look and sound the same. However, there is often a complicated rhythm to the crashing surf; its loudness fluctuates with an overall pattern known as surf beat. Surf beat is a sign that the ocean’s surface is a busy place; it’s actually carrying more than one traveling wave at a time, and these various waves all contribute to the surf. To understand how multiple traveling waves produce surf beat, let’s consider a simple case. Suppose that two traveling waves are heading toward shore and that they have equal amplitudes but different wavelengths. Such a situation can easily arise when winds over two portions of the ocean produce two different traveling waves that later overlap. Since they are sharing the ocean’s surface, they are superposed on one another.
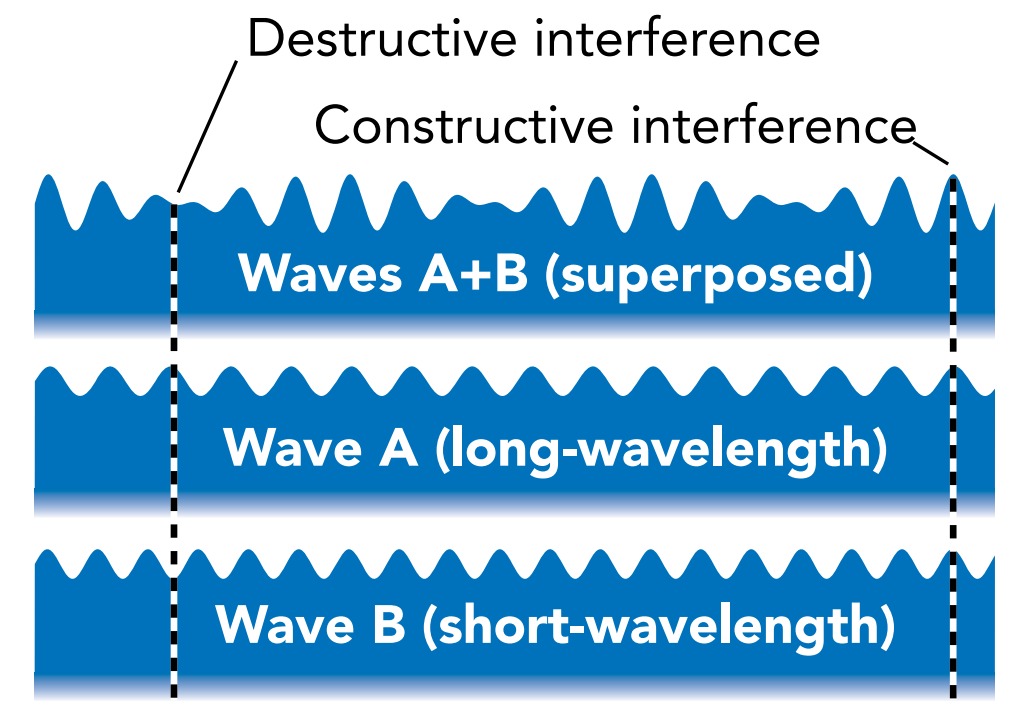
Because these traveling waves are different, their patterns of crests and troughs can’t coincide everywhere. Instead, these waves experience interference, their overlying patterns enhance one another at some locations and cancel one another at other locations. Wherever the two waves are in phase, that is, whenever their crests or troughs coincide, they experience constructive interference—the waves act together to produce enormous crests or troughs. Wherever the two waves are out of phase, that is, whenever the crest of one wave coincides with the trough of the other wave, they experience destructive interference—the waves oppose one another to produce muted or absent crests or troughs. The result is an interference pattern, an intricate structure that spreads across space and time when waves are superposed. This interference pattern on the ocean’s surface moves and evolves as the traveling waves head toward shore, and it leaves its impression on the crests that eventually break on the beach. Since these crests are no longer equal in height, they exhibit the complicated rhythm of surf beat. When you listen to that beat, you’re hearing the consequence of superposition and the interference of waves.