Musical Instruments
Music is an important part of human expression. Although what qualifies as music is a matter of taste, it always involves sound and often involves instruments.
Sound and Music
To understand how instruments work, we need to know a bit more about sound and music. In air, sound consists of density waves, patterns of compressions and rarefactions that travel outward rapidly from their source. When a sound passes by, the air pressure in your ear fluctuates up and down about normal atmospheric pressure. Even when these fluctuations have amplitudes less than a millionth of atmospheric pressure, you hear them as sound.

When the fluctuations are repetitive, you hear a tone with a pitch equal to the fluctuation’s frequency. Pitch is the frequency of a sound. A bass singer’s pitch range extends from 80 to 300 Hz, while that of a soprano singer extends from 300 to 1100 Hz. Musical instruments can produce tones over a much wider range of pitches, but we can hear only those between about 30 and 20,000 Hz, and that range narrows as we get older.
Most music is constructed around intervals, the frequency ratio between two different tones. This ratio is found by dividing one tone’s frequency by that of the other. Our hearing is particularly sensitive to intervals, with pairs of tones at equal intervals sounding quite similar to one another. For example, a pair of tones at 440 and 660 Hz sounds similar to a pair at 330 and 495 Hz because they both have the interval 3/2.
The most important interval in virtually all music is 2/1, or an octave. Tones that differ by a factor of 2 in frequency sound. The octave is so important that it structures the entire range of audible pitches. Most of the subtle interplay of tones in music occurs in intervals of less than an octave, less than a factor of 2 in frequency. Thus most traditions build their music around the intervals that lie within a single octave, such as 5/4 and 3/2. They pick a particular standard pitch and then assign notes at specific intervals from this standard pitch. This arrangement repeats at octaves above and below the standard pitch to create a complete scale of notes.
A Violin’s Vibrating String
The tones produced by a violin begin as vibrations in its strings. On their own, these strings are limp and shapeless so they rely on the violin’s rigid body and neck for structure. The violin subjects its strings to tension, outward forces that act to stretch it, and this tension gives each string an equilibrium shape—a straight line.
To see that a straight violin string is in equilibrium, think of it as being composed of many individual pieces that are connected together in a chain. Tension exerts a pair of outward forces on each piece of the string; its neighboring pieces are pulling that piece toward them. Since the string’s tension is uniform, these two outward forces sum to zero; they have equal magnitudes but point in opposite directions. With zero net force on each of its pieces, the straight string is in equilibrium.
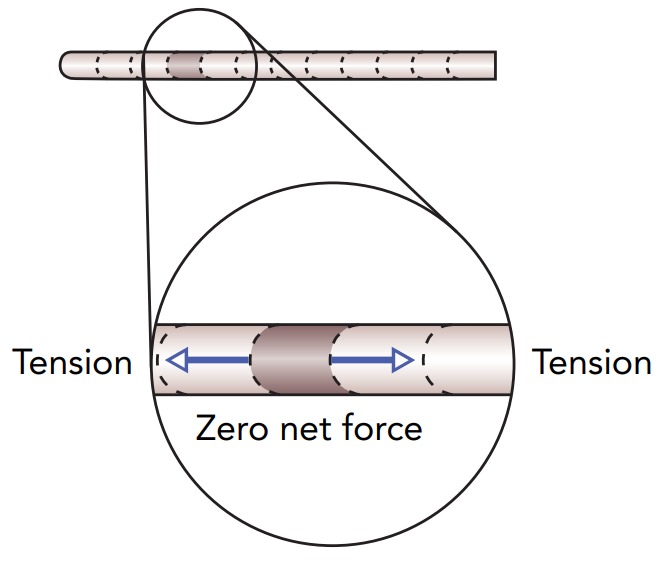
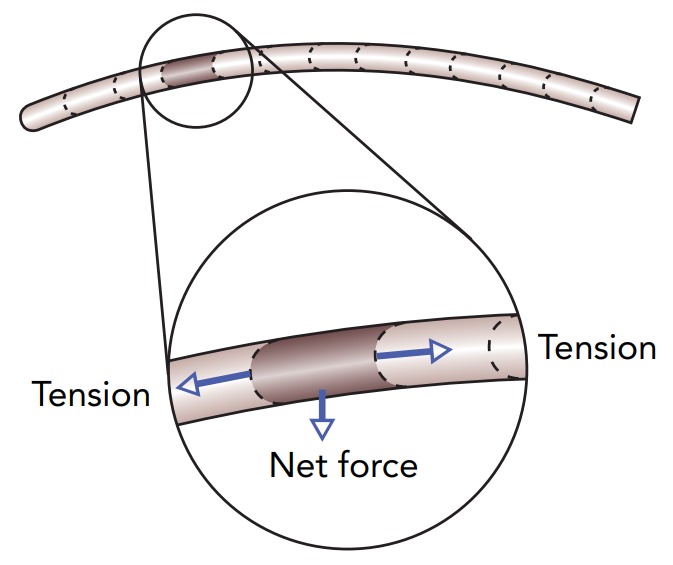
When the string is curved, however, the pairs of outward forces no longer sum to zero. Although those outward forces still have equal magnitudes, they now point in slightly different directions. As a result, each piece experiences a small net force. The net forces on its pieces are restoring forces because they act to straighten the string. If you distort the string and release it, these restoring forces will cause the string to vibrate about its straight equilibrium shape in a natural resonance. The string’s restoring forces are special; the more you curve the string, the stronger the restoring forces on its pieces become. In fact, the restoring forces are springlike forces—they increase in proportion to the string’s distortion—so the string is a form of harmonic oscillator!
It can bend and vibrate in many distinct modes, or basic patterns of distortion, each with its own period of vibration. Nonetheless, the string retains the most important feature of a harmonic oscillator: the period of each vibrational mode is independent of its amplitude. Thus a violin string’s pitch doesn’t depend on how hard it’s vibrating.
In this fundamental mode, the violin string behaves as a single harmonic oscillator. As with any harmonic oscillator, its vibrational period depends only on the stiffness of its restoring forces and on its inertia. Either stiffening the violin string or reducing its mass will quicken its fundamental vibration and increase its fundamental pitch.
A violin has four strings, each with its own stiffness and mass, and therefore with its own fundamental pitch. In a tuned violin, the notes produced by these strings are G3 (196 Hz), D4 (294 Hz), A4 (440 Hz), and E5 (660 Hz). The G3 string, which vibrates rather slowly, is the most massive. It’s usually made of gut, wrapped in a coil of heavy metal wire. The E5 string, on the other hand, must vibrate quite rapidly and so needs to have a low mass. It’s usually a thin steel wire.
You tune a violin by adjusting the tension in its strings using the pegs in its neck and tension adjusters on the tailpiece. Tightening the string stiffens it by increasing both the outward forces on its pieces and the net forces they experience during a distortion. A string’s fundamental pitch also depends on its length. Shortening the string both stiffens it and reduces its mass, so its pitch increases. That stiffening occurs because a shorter string curves more sharply when it’s displaced from equilibrium and therefore subjects its pieces to larger net forces. This dependence on length allows you to raise a string’s pitch by pressing it against the fingerboard in the violin’s neck and effectively shortening it. Part of a violinist’s skill involves knowing exactly where on the string to press it against the fingerboard to produce a particular note.
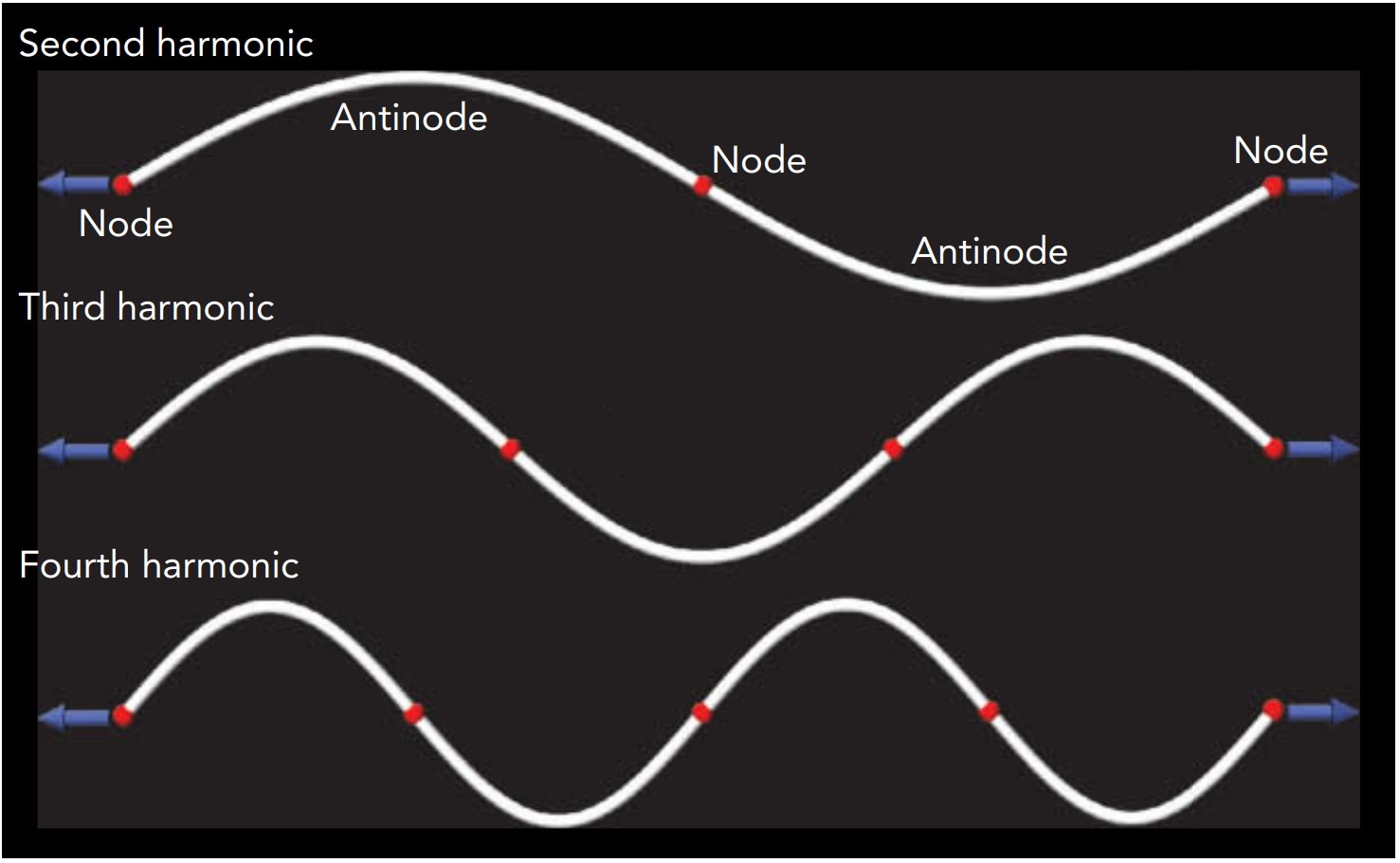
The string’s fundamental mode is a particularly simple wave, a standing wave, which is a wave with fixed nodes and antinodes. A standing wave’s basic shape doesn’t change with time; it merely scales up and down rhythmically at a particular frequency and amplitude (its peak extent of motion). Most important, the standing wave. Although this wave extends along the string, its associated oscillation is perpendicular to the string and therefore perpendicular to the wave itself. A wave in which the underlying oscillation is perpendicular to the wave itself is called a transverse wavedoesn’t travel along the string.

The fundamental vibrational mode isn’t the only way in which a violin string can vibrate. The string also has higher-order vibrational modes in which the string vibrates as a chain of shorter strings arcing in alternate directions. Each of these higher-order vibrational modes is another standing wave, with a fixed shape that scales up and down rhythmically at its own frequency and amplitude. a string’s vibrational frequency is inversely proportional to its length, so halving its length doubles its frequency. Frequencies that are integer multiples of the fundamental pitch are called harmonics, so this half-string vibration occurs at the second harmonic pitch and is called the second harmonic mode. The violin’s sound is thus a rich mixture of the fundamental tone and the harmonics known as timbre.
When a violin string is vibrating in several modes at once, its shape and motion are complicated. The individual standing waves add on top of one another, a process known as superposition. Each vibrational mode has its own amplitude and therefore its own loudness contribution to the string’s timbre.
You play a violin by drawing a bow across its strings. The bow consists of horsehair, pulled taut by a wooden stick and coated with rosin, a sticky substance based on pine sap. This coated horsehair exerts frictional forces on the strings as it moves across them. Most important, however, is that it exerts much larger static frictional forces than sliding ones. As the sticky bow hairs rub across a string, they grab the string and push it forward with static friction. Eventually the string’s restoring force overpowers static friction, and the string suddenly starts sliding backward across the hairs. Because the hairs exert little sliding friction, the string completes half a vibrational cycle with ease. As it stops to reverse direction, however, the hairs grab the string again and begin pushing it forward. This process repeats over and over.
Each time the bow pushes the string forward, it does work on the string and adds energy to the string’s vibrational modes. This process is an example of resonant energy transfer, in which a modest force doing work in synchrony with a natural resonance can transfer a large amount of energy to that resonance. The amount of energy the bow adds to each vibrational mode depends on where it crosses the violin string. When you bow the string at the usual position, you produce a strong fundamental vibration and a moderate amount of each harmonic. Bowing the string nearer its middle reduces the string’s curvature, weakening its harmonic vibrations and giving it a more mellow sound. Bowing the string nearer its end increases the string’s curvature, strengthening its harmonic vibrations and giving it a brighter sound.

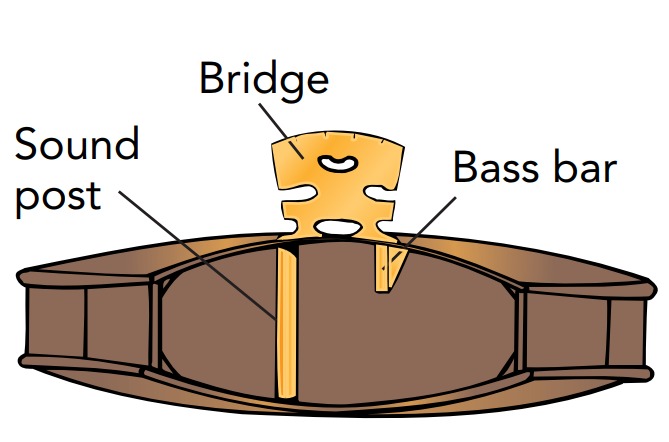
As a bowed string vibrates across the violin’s belly, it exerts a torque on the bridge about the sound post. The bridge rotates back and forth, causing the bass bar and belly to move in and out. The belly’s motion produces most of the violin’s sound. Some of this sound comes directly from the belly’s outer surface, and the rest comes from its inner surface and must emerge through its S-shaped hole
Musical Instruments
Sonometry (Acoustics)
Landmines were first used during the first World War to stop tanks from rolling right over their battle lines. Explosive material, TNT was developed by the second World War, in 1939 and was deployed to develop much better antitank mines. However, advancing troops soon found they could remove the antitank mines by hand. This leads to the development of mines designed to explode under the pressure of a human foot. These mines were laid close to the antitank mines to protect them. During the early 1960s, United States began using new, smaller, remotely delivered antipersonnel mines, which could be dropped by thousands from airplanes over a broad region. These mines were used to stop the flow of soldiers and supplies between North and South Vietnam . These methods of delivery means that, mine locations could not be mapped. The same method of randomly scattering mine was used by the Soviet Union during the its invasion of Afghanistan in the 1980s.
Nowadays, The use of landmines during the armed conflict is one of the most dangerous problems that facing the Human being, since they have a devastating impact on the individual lives. They kill innocent civilian people and cause a severe social and economic consequences, particularly for a country attempting to rebuild after the end of the war. The presence of mines can leave large portions of the land unusable. Farmlands, grazing pastures and other food–producing areas my be rendered in accessible and , as a result, the ability of a community to feed itself is impaired . Mine clearance , although essential, is slow, dangerous and an expensive process. According to official figures, more than 110 million landmine have been laid in several countries, among them is Egypt, with about 23 million landmine lie buried in the Northern parts of the Western desert and Northern and Western parts of the Sinai. Recently, mines become also a weapon of choice in smaller skirmishes and civil war, largely because they are so cheap and easy to obtain. Instead of being used to protect military positions, mines are often used to terrorize and demoralize civilians. Bosnia and Crotia now have millions to deal with many of them planted around wells, rivers, power sources, buildings and other high-traffic areas. Detecting of mines is the real problem before defusing them. Rarely, if ever armies leave accurate maps of locations of mines. Detectors based on metal detection pick up mines made of metal , but , most modern mines are made of plastics. Their size (some are as small 2.5 cm wide) also makes them difficult to pinpoint. Others based on visible and infrared observation , on microwave detection and on nuclear techniques are able to detect a mines from one of its characteristics

Conventional ultrasound detection involves the emission of a sound wave with a frequency higher than 20 KHZ into a medium. This sound wave reflects on boundaries between material with different acoustical properties. Therefore, ultrasound systems effectively penetrate very wet and heavy ground such as clay, rendering them complementary to CPR. However, ultrasound system counter problems at interface of air and ground. Ultrasound detectors are used to detect AP mines submerged in water, a simulation of mines thrown into rice fields. The above mentioned techniques are mainly used for detecting trace explosives, interest is growing in techniques for detecting bulk explosives. These techniques are used in security or nondestructive testing . Applying these techniques to mine detection, which requires:
- One-sided sensor configuration,
- Operator security ,
- Equipment portability , and
- Extensive soil penetration .
Acoustic/seismic methods
Acoustic/seismic methods look for mines by “vibrating” them with sound or seismic waves that are introduced into the ground. This process is analogous to tapping on a wall to search for wooden studs: materials with different properties vibrate differently when exposed to sound waves. These methods are unique among detection methods that identify the mine casing and components in that they are not based on electromagnetic properties.
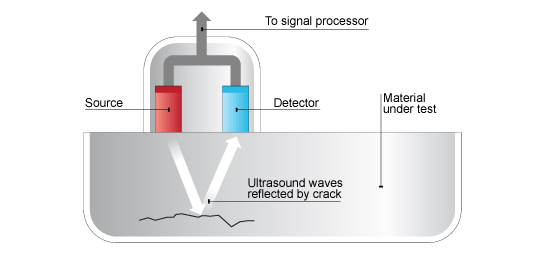
Acoustic/seismic mine detection systems typically generate sound (above ground) from an off-the-shelf loudspeaker, although there are many possible configurations. Some of the acoustic energy reflects off the ground surface, but the rest penetrates the ground in the form of waves that propagate through the soil. When an object such as a mine is buried, some of the energy reflects upward toward the ground surface, causing vibration at the surface. Specialized sensors can detect these vibrations without contacting the ground. A variety of different kinds of sensors (laser Doppler vibrometers, radars, ultrasonic devices, microphones) have been tried. Researchers have field tested acoustic/seismic methods for landmine detection on approximately 300 buried antitank and antipersonnel mines and several hundred square meters of clutter locations at Army field sites in Virginia and Arizona. Initial tests focused on antitank mines and yielded high probabilities of detection and low false alarm rates. For example, in one test, the acoustic system identified 18 of 19 mines buried in dirt and gravel, yielding a probability of detection of 95 percent. There was only one false alarm in the test, even though the test site was seeded with clutter items that had confounded a GPR system. When the system was modified with advanced signal-processing algorithms, the false alarm rate dropped to zero.
Acoustic-to-seismic (A/S) coupling–based mine detection is based on the ability of sound to penetrate the ground and excite resonances in buried compliant objects. Sound produced in the air efficiently couples into the first 0.5 m of the soil because of the porous nature of weathered ground resulting in acoustic vibrations that are sensitive to the presence of buried mines. This phenomenon has been termed “acoustic-to-seismic coupling” in the research literature. Off-the-shelf loudspeakers are used as the sound source and readily available laser Doppler vibrometers (LDVs) are used to measure the increased ground vibrations due to the presence of the buried mine. The use of airborne acoustics for mine detection exploits three new phenomena that previously have not been explored for the purpose of buried mine detection. First, a landmine is a man-made, acoustically compliant object that is much more compliant than soils. This results in a high-vibration contrast between soils and buried mines that does not occur because of the presence of rocks, roots, and other man-made solid objects, such as concrete and metal. Second, the mine is a nonporous object that offers additional contrast to the porous soil in the presence of coupled sound. Third, the interface between a mine and the soil has been shown to be nonlinear; the interface between the soil and the mine is not continuous when vibrating. This phenomenon results from the strong acoustic compliance of the mine compared with soil. This nonlinear phenomenon allows for unique measurements that are in theory absolutely free of false alarms.
The essence of the acoustic/seismic approach is to excite low frequency (typically below 1,000 Hz) vibration of a buried mine and measure surface “vibration signature” above the mine using remote sensors. Excitation of a mine and surrounding soil is achieved by using airborne (acoustic) and/or solid-borne (seismic) waves. Remote sensing is achieved with laser Doppler, microwave, or ultrasonic vibrometers. The technique does not depend on the material from which the mine is fabricated, whether it be metal, plastic, wood, or any other material. It depends on the fact that a mine is a “container” whose purpose is to contain explosive materials and associated detonation apparatus. The mine container is in contact with the soil in which it is buried. The container is an acoustically compliant article whose compliance is notably different from the compliance of the surrounding soil. Dynamic interaction of the compliant container and the soil on top of it leads to specific linear and nonlinear effects used for mine detection and discrimination. The mass of the soil on top of a compliant container creates a classical mass-spring system with a well-defined resonance response. In addition, the connection between mass (soil) and spring (mine) is not elastic (linear) but rather nonlinear because of the separation of the soil/mine interface in the tensile phase of applied dynamic stress. These two effects, constituting the mine’s “vibration signature,” have been measured in numerous laboratory and field tests, which proved that the resonance and nonlinear responses of a mine/soil system can be used for detection and discrimination of buried mines. Thus, the fact that the mine is buried is turned into a detection advantage. Because the seismo-acoustic technique intrinsically detects buried “containers,” it can discriminate mines from noncompliant false targets, such as rocks, tree roots, chunks of metal, bricks, etc. This was also confirmed experimentally in laboratory and field tests.
Strengths
Acoustic/seismic sensors are based on completely different physical effects than any other sensor. For example, they sense differences in mechanical properties of the mine and soil, while GPR and EMI sensors detect differences in electromagnetic properties. Thus, acoustic/ seismic sensors would complement existing sensors well. Acoustic/seismic systems also have the potential for very low false alarm rates. In experiments to date, false alarms from naturally occurring clutter, such as rocks and scrap metal, have been extremely low (although such hollow clutter items as soda bottles and cans would cause false alarms because the resonance patterns of these objects are similar to those of mines). An additional strength is that, unlike GPR systems, these sensors are unaffected by moisture and weather, although frozen ground may limit the sensor’s capability.
Limitations
The greatest limitation of acoustic/seismic systems is that they do not detect mines at depth because the resonant response attenuates significantly with depth. With current experimental systems, mines deeper than approximately one mine diameter are difficult to find. Also problematic is the slow speed of existing systems. Speed currently is limited by the displacement sensor, which senses the vibrations at the surface caused by the sound waves. These displacements are very small (less than 1 µm) and are thus difficult to measure quickly in the adverse conditions of a minefield. The required scan time for locating antipersonnel mines may range from 125 to 1,000 seconds per square meter. However, a number of methods are being investigated to speed up the detection process. For example, an array of N sensors will speed the system by a factor of N. Small prototypes of such arrays have been developed and can be expanded and improved with further work. An additional limitation of existing systems is that moderate to heavy vegetation can interfere with the laser Doppler vibrometers that are commonly used to sense the vibrations at the ground surface. A new type of sensor could be developed, however, to overcome this flaw.