Pressure plays an important role in aerosol cans, steam engines, firecrackers, and even the weather; buoyancy supports ships on the water and keeps oil above vinegar in a bottle of salad dressing.
First, we examine two things from the world around us: (1) balloons and (2) water distribution. In Balloons, we explore how the concepts of pressure and buoyancy help explain how Earth’s atmosphere keeps hot-air and helium balloons from falling to the ground. In Water Distribution, we see both how pressure propels water through plumbing and the ways in which water can contain energy.
Balloons
Because gravity gives every object near Earth’s surface a weight proportional to its mass, objects fall when you drop them. Why then does a helium-filled balloon—which, after all, is just another object with a mass and a weight—sail upward into the sky when you let go of it?
The layer of air that sits atop Earth’s surface and is held in place by gravity. Since this air is difficult to see and moves out of our way so easily, we often forget that it’s there. But air sometimes makes itself noticeable. When you ride a bicycle, you feel its forces; when you blow up a beach ball, you see that it takes up space. And when you release a helium balloon, air lifts the balloon upward.
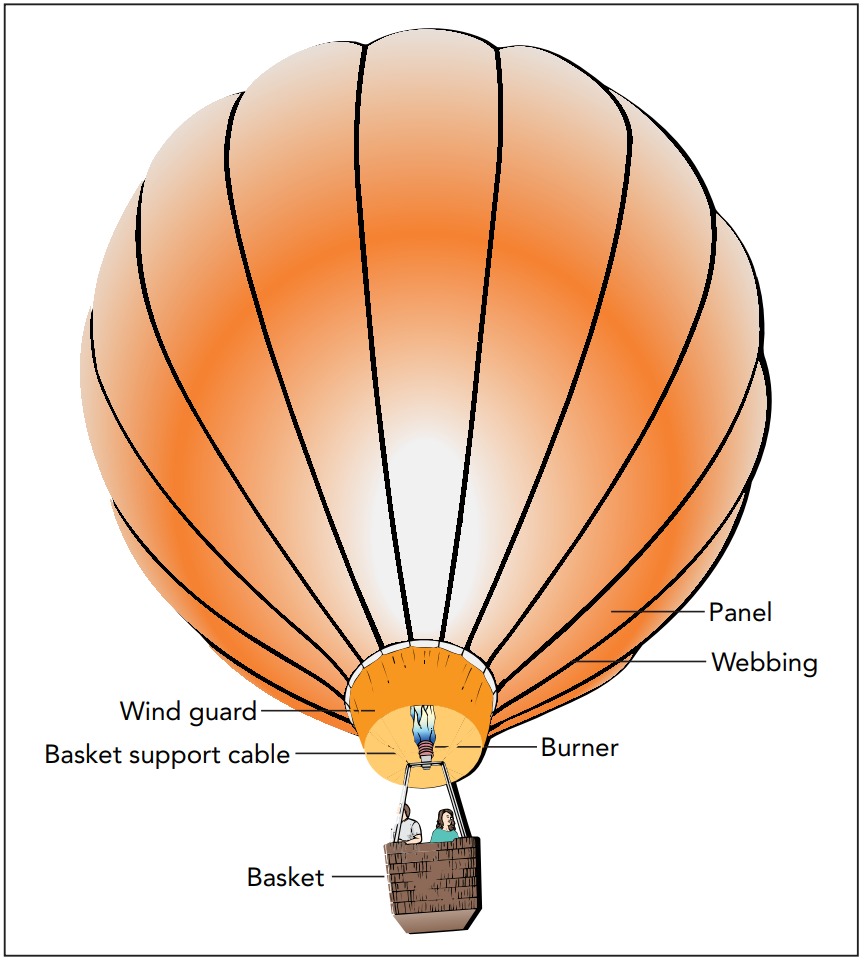
Air Pressure
Hot-air and helium balloons don’t really defy gravity. In fact, they’re not even close to weightless. But even though these balloons may weigh hundreds of pounds, something supports their weight and holds them aloft—the surrounding air. Air has weight and mass. air has no fixed shape or size. Air is compressible, that is, you can squeeze a certain mass of it into almost any space.
This flexibility of size and shape originates in the microscopic nature of air. Air is a gas, a substance consisting of tiny, individual particles that travel around independently. These individual particles are atoms and molecules. An atom is the smallest portion of an element that retains all the chemical characteristics of that element; a molecule, an assembly of two or more atoms, is the smallest portion of a chemical compound that retains all the characteristics of that compound. A molecule’s atoms are held together by chemical bonds, linkages formed by electromagnetic forces between the atoms.
Air particles are extremely small, less than 1 millionth of a millimeter in diameter. Most are nitrogen and oxygen molecules, but others include carbon dioxide, water, methane, and hydrogen molecules, and also argon, neon, helium, krypton, and xenon atoms. Those particular atoms, which don’t make strong chemical bonds and rarely form molecules, are called inert gases because of their chemical inactivity.
Air’s individual particles have such minuscule masses that, even at room temperature, they exhibit frenetic thermal motion which keeps them moving, spinning and colliding with each other. Their frequent collisions prevent them from making much progress in any particular direction and, between collisions, they travel in nearly straight line paths because gravity doesn’t have time to make them fall very far. This vigorous thermal motion spreads the air particles apart, so they don’t accumulate on the ground.
The air particles enclosed in a container exert a force on that wall and among each other. Although the individual forces are tiny, the number of particles is not, and together they produce a large average force. The size of this total force depends on the wall’s surface area; the larger its surface area, the more average force it experiences. the average force the air exerts on each unit of surface area, a quantity called pressure.
\[ pressure =\frac{force}{surface~area}\]
Pressure is measured in units of force per area. the SI unit of pressure is the newton per square meter. . This unit is also called the Pascal (abbreviated Pa), after French mathematician and physicist Blaise Pascal. One pascal is a small pressure. The air around you has a pressure of about 100,000 Pa, so it exerts a force of about 100,000 N on a 1 \(m^{2}\) surface. Air also pushes on any object immersed in it.
Pressure, Density, and Temperature
Since air pressure is produced by bouncing air particles, it depends on how often, and how hard, those particles hit a particular region of surface. The more frequent or harder the impacts, the greater is the air pressure.
Air’s pressure is thus proportional to its density, that is, its mass per unit of volume:
\[ density =\frac{mass}{volume}\]
the SI unit of density is the kilogram per meter3. The air around you has a density of about 1.25 \(kg/m^{3}\). Water has a much greater density of about 1000 kg/m3.
We can also increase the rate at which air particles hit a surface by speeding them up. The hotter the air, the more thermal energy it contains and the faster its particles move. Thermal energy is a combination of internal kinetic energy in the particles’ random thermal motion and internal potential energy stored as part of that random thermal motion. Since air particles are essentially independent, except, during collisions, nearly all of air’s thermal energy is internal kinetic energy. An air particle’s kinetic energy is proportional to the square of its speed. Air pressure is proportional to the average internal kinetic energy of its particles.
Temperature measures this average internal kinetic energy per particle; the hotter the air, the larger is the average internal kinetic energy per particle and the greater the air’s pressure. That’s why the tire’s air pressure increases on hot days and when it heats up during highway driving.
The most convenient scale for relating air’s temperature to air’s pressure is the absolute temperature scale, in which the zero of the temperature scale is absolute zero, the temperature at which an object contains zero thermal energy. At absolute zero (−273.15 °C or −459.67 °F), air contains no internal kinetic energy at all and has no pressure. air’s pressure is proportional to its temperature at an absolute temperature scale. The SI scale of absolute temperature is the Kelvin scale (K). The Kelvin scale is identical to the Celsius scale, except that it’s shifted so that 0 K is equal to −273.15 °C.
Since air pressure is proportional to both the air’s density and its absolute temperature, we can express the relationship among these quantities in the following way:
\[pressure \propto density \times absolute ~temperature. \]
This relationship is useful because it allows us to predict what will happen if we change the temperature or density of a specific gas, such as air. The relationship does have its limitations; in particular, it doesn’t work if we compare the pressures of two different gases, such as air and helium, which differ in their chemical compositions. If the temperature drops too low, the particles begin to stick together to form a liquid and the pressure-temperature relationship becomes invalid.
Despite its limitations, however, this simple relationship between pressure, density, and temperature will prove useful in understanding how hot-air balloons float. It will help us understand the basic structure of Earth’s atmosphere, the origins of the upward force that keeps a hot-air balloon aloft, and the reason why hot air rises.
Earth’s Atmosphere
Most of the mass of Earth’s atmosphere is contained in a layer less than 6 km (4 miles) thick. Since Earth is 12,700 km (7,900 miles) in diameter, this layer is relatively thin.
The atmosphere stays on Earth’s surface because of gravity. Every air particle has a weight. the particles of air keep returning toward the Earth’s surface. Although the particles are moving too fast for gravity to affect their motions significantly over the short term, gravity works slowly to keep them relatively near the Earth’s surface. An air particle may appear to travel in a straight line at first, but it will arc over and begin to fall downward eventually. Only the lightest and fastest moving particles in the atmosphere—hydrogen molecules and helium atoms—occasionally manage to escape from Earth’s gravity and drift off into interplanetary space.
While gravity pulls the atmosphere downward, air pressure pushes the atmosphere upward. As the air particles try to fall to Earth’s surface, their density increases and so does their pressure. It’s this air pressure that supports the atmosphere.
The air near the ground supports the weight of several kilometers of air above it, giving it a density of about 1.25 \(kg/m^{3}\)
and a pressure of about 100,000 Pa. At higher altitudes, however, the air’s density and pressure are reduced, since there is less atmosphere overhead and the air doesn’t have to support as much weight. High-altitude air is thus “thinner” than low-altitude air.
The Lifting Force on a Balloon: Buoyancy
The air in Earth’s atmosphere is a fluid, a shapeless substance with mass and weight. This air has pressure and exerts forces on the surfaces it touches; that pressure is greatest near the ground and decreases with increasing altitude. Air pressure and its variation with altitude allow air to lift hot-air and helium balloons through an effect known as buoyancy.
Buoyancy was first described more than 2000 years ago by the Greek mathematician Archimedes (287–212 BC). Archimedes realized that an object partially or wholly immersed in a fluid is acted on by an upward buoyant force equal to the weight of the fluid it displaces. Archimedes’ principle is actually very general and applies to objects floating or submerged in any fluid, including air, water, or oil. The buoyant force originates in the forces that a fluid exerts on the surfaces of an object.
Without gravity, the forces would cancel each other perfectly because the pressure of a stationary fluid would be uniform throughout. But gravity causes a stationary fluid’s pressure to increase with distance in the downward direction; the fluid has a downward pressure gradient. When nothing is moving, the air pressure beneath an object is always greater than the air pressure above it. Thus air pushes upward on the object’s bottom more strongly than it pushes downward on the object’s top, and the object consequently experiences an upward overall force from the air—a buoyant force.
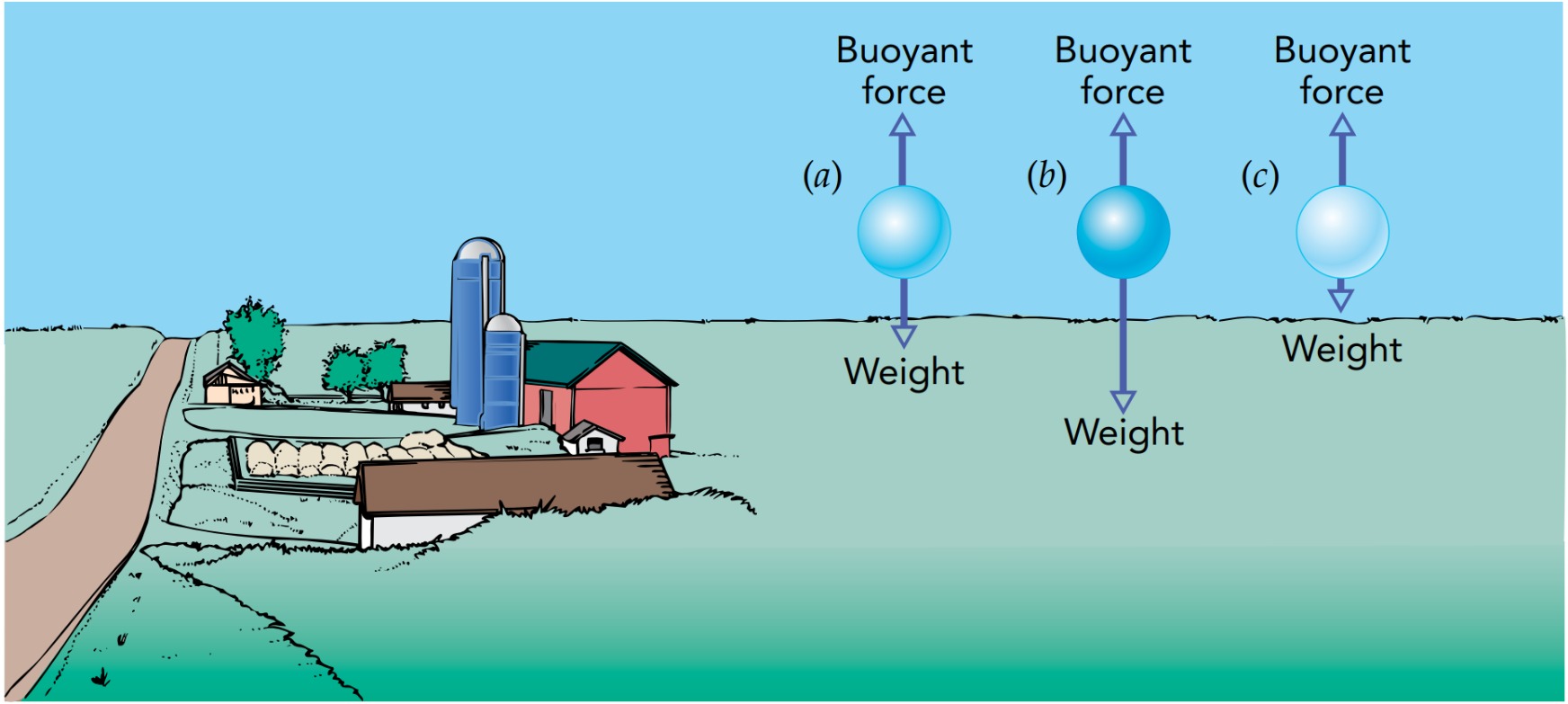
The buoyant force is equal in magnitude to the weight of the fluid that the object displaces. Since the buoyant force is exerted by the surrounding fluid, not the object, it doesn’t depend on the object’s composition. A balloon filled with helium will experience the same buoyant force as a similar balloon filled with water or lead or even air. So replacing the object with a similarly shaped portion of fluid will leave the buoyant force on it unchanged.
This buoyant principle explains why some objects float while others sink. An object placed in a fluid experiences two forces: its downward weight and an upward buoyant force. If its weight is more than the buoyant force, it will accelerate downward. If its weight is less than the buoyant force, it will accelerate upward. If the two forces are equal, it won’t accelerate at all and will maintain a constant velocity. An object that has an average density greater than that of the surrounding fluid sinks, while one that has a lesser average density floats.
Hot-Air Balloons
Since air is very light, with a density of only 1.25 \(kg/m^{3}\), few objects float in it. One of these rare objects is a balloon with a vacuum inside it. Assuming that the balloon has a very thin outer shell or envelope, it will weigh almost nothing and have an average density near zero. Because its negligible weight is less than the upward buoyant force it experiences, the empty balloon will float upward nicely.
Unfortunately, this empty balloon won’t last long. Because it’s surrounded by atmospheric pressure air, each square meter of its envelope will experience an inward force of 100,000 N. With nothing inside the balloon to support its envelope against this crushing force, it will smash flat. A thick, rigid envelope might be able to withstand the pressure of the surrounding air, but then the balloon’s average density would be large and it would sink. So an empty balloon won’t work.
What will work is a balloon filled with something that exerts an outward pressure on the envelope equal to the inward pressure of the surrounding air. Then each portion of the envelope will experience zero net force and the balloon will not be crushed. We could fill the balloon with outside air, but that would make its average density too high. Instead, we need a gas that has the same pressure as the surrounding air but a lower density.
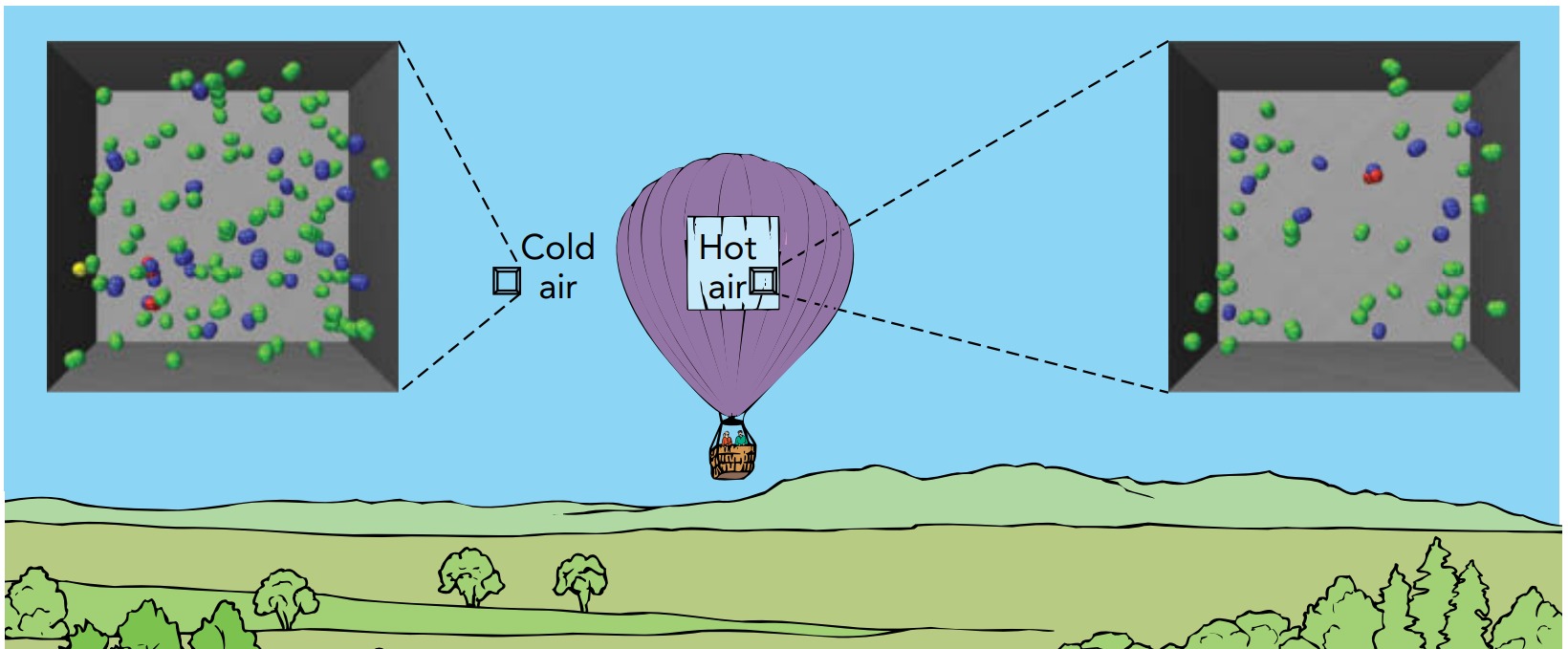
One gas that has a lower density at atmospheric pressure is hot air. Filling our balloon with hot air takes fewer particles than filling it with cold air since each hot-air particle is moving faster and contributes more to the overall pressure than does a cold-air particle. A hot-air balloon contains fewer particles, has less mass, and weighs less than it would if it contained cold air. The buoyant force it experiences is larger than its weight, and up it goes.
Because the air pressure inside a hot-air balloon is the same as the air pressure outside the balloon, the air has no tendency to move in or out and the balloon doesn’t need to be sealed. A large propane burner, located beneath the balloon’s open end, heats the air that fills the envelope. The heated air expands to fill more volume at the same pressure and some of it flows out the balloon’s open bottom. The hotter the air in the envelope, the lower its density and the less the balloon weighs. The balloon’s pilot controls the flame so that the balloon’s weight is very nearly equal to the buoyant force on the balloon. If the pilot raises the air’s temperature, particles leave the envelope, the balloon’s weight decreases, and the balloon rises. If the pilot allows the air to cool, particles enter the envelope, the balloon’s weight increases, and the balloon descends.
Even if the pilot heats the air until it is very hot, the balloon won’t rise upward forever. As the balloon ascends, the air becomes thinner and the pressure decreases both inside and outside the envelope. Although the balloon’s weight decreases as the air thins out, the buoyant force on it decreases even more rapidly and it becomes less effective at lifting its cargo. When the air becomes too thin to lift the balloon any higher, the balloon reaches a flight ceiling above which it can’t rise. For each hot-air temperature, then, there is a cruising altitude at which the balloon will hover. When the balloon reaches that altitude, it’s in a stable equilibrium. If the balloon shifts downward for some reason, the net force on it will be upward; if it shifts upward, the net force on it will be downward.
Because a balloon’s fabric envelope ages quickly at high temperatures, the balloon’s air mustn’t be heated above about 120 °C. Lower air temperatures prolong the life of the envelope, and a pilot usually tries to reduce the air temperature required by reducing the weight of the balloon’s cargo.
Helium Balloons
Helium atoms are much lighter than air particles. When they have equal pressures and temperatures, helium gas and air also have equal particle densities (number of particles per unit of volume). Since each helium atom weighs 14% as much as the average air particle, 1 \(m^{3}\) of helium weighs only 14% as much as 1 m3 of air. Thus a helium-filled balloon has only a fraction of the weight of the air it displaces, and the buoyant force carries it upward easily.
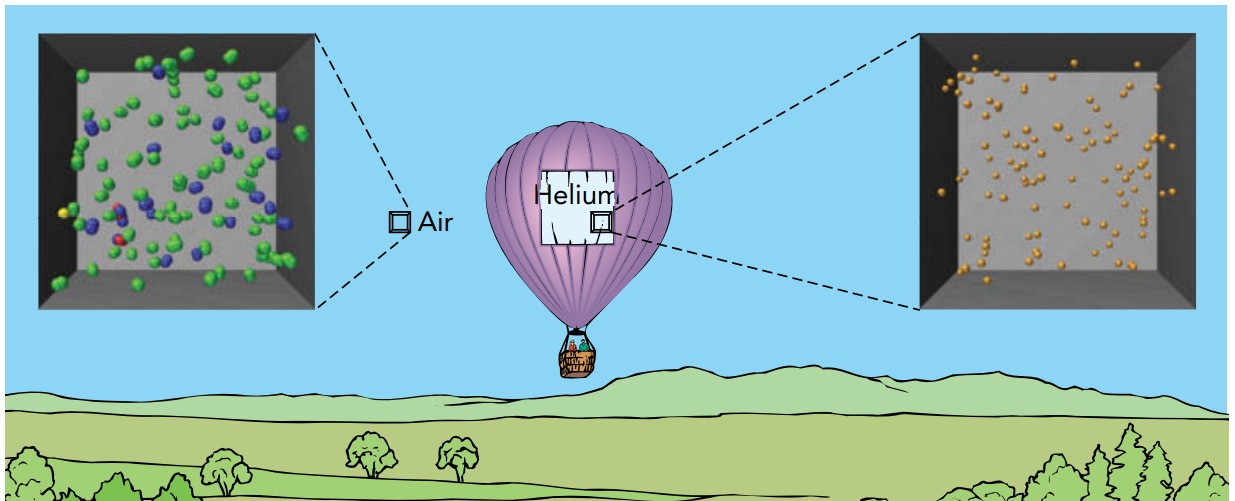
Why should air and helium have the same particle densities whenever their pressures and temperatures are equal?
Because a gas particle’s contribution to the pressure doesn’t depend on its mass (or weight). At a particular temperature, each particle in a gas has the same average internal kinetic energy in its translational motion, regardless of its mass. Although a helium atom is much less massive than a typical air particle, the average helium atom moves much faster and bounces more often. As a result, lighter but faster-moving helium atoms are just as effective at creating pressure as heavier but slower-moving air particles.
Thus, if you allow the helium atoms inside a balloon to spread out until the pressures and temperatures inside and outside the balloon are equal, the particle densities inside and outside the balloon will also be equal. Since the helium atoms inside the balloon are lighter than the air particles outside it, the balloon weighs less than the air it displaces, and it will be lifted upward by the buoyant force.
The pressure of a gas is proportional to the product of its particle density and its absolute temperature, as the following formula indicates:
\[pressure \propto particle density \times absolute ~temperature\]
This proportionality holds regardless of the gas’s chemical composition which is also known as ideal gas law. This law relates pressure, particle density, and absolute temperature for a gas in which the particles are perfectly independent. The constant of proportionality is the Boltzmann constant, with a measured value of \(1.381 \times 10^{−23}\) \(Pa · m^{3}\) /(particle · K). Using the Boltzmann constant, the ideal gas law can be written as a word equation:
\[pressure = Boltzmann~ constant · particle~ density · absolute~ temperature\]
in symbols:
\[p = k · \rho_{particle} · T\]
Helium isn’t the only “lighter-than-air” gas. Hydrogen gas, which is half as dense as helium, is also used to make balloons float. A balloon’s lifting capacity is the difference between the upward buoyant force it experiences and its downward weight. Although the gas in a hydrogen balloon weighs half that in a similar helium balloon, the balloons experience the same buoyant force. Thus the hydrogen balloon’s lifting capacity is only slightly more than that of the helium balloon. Hydrogen’s main advantage is that it’s cheap and plentiful, while helium is scarce. Hydrogen is also dangerously flammable, so it’s avoided in situations where safety is important. However, even helium-filled airships can be damaged by air turbulence in bad weather.