Water Distribution
we will examine how plumbing distributes water, we’ll see that pressure, density, and weight are just as important in plumbing. we’ll focus on the causes of water’s motion through plumbing.
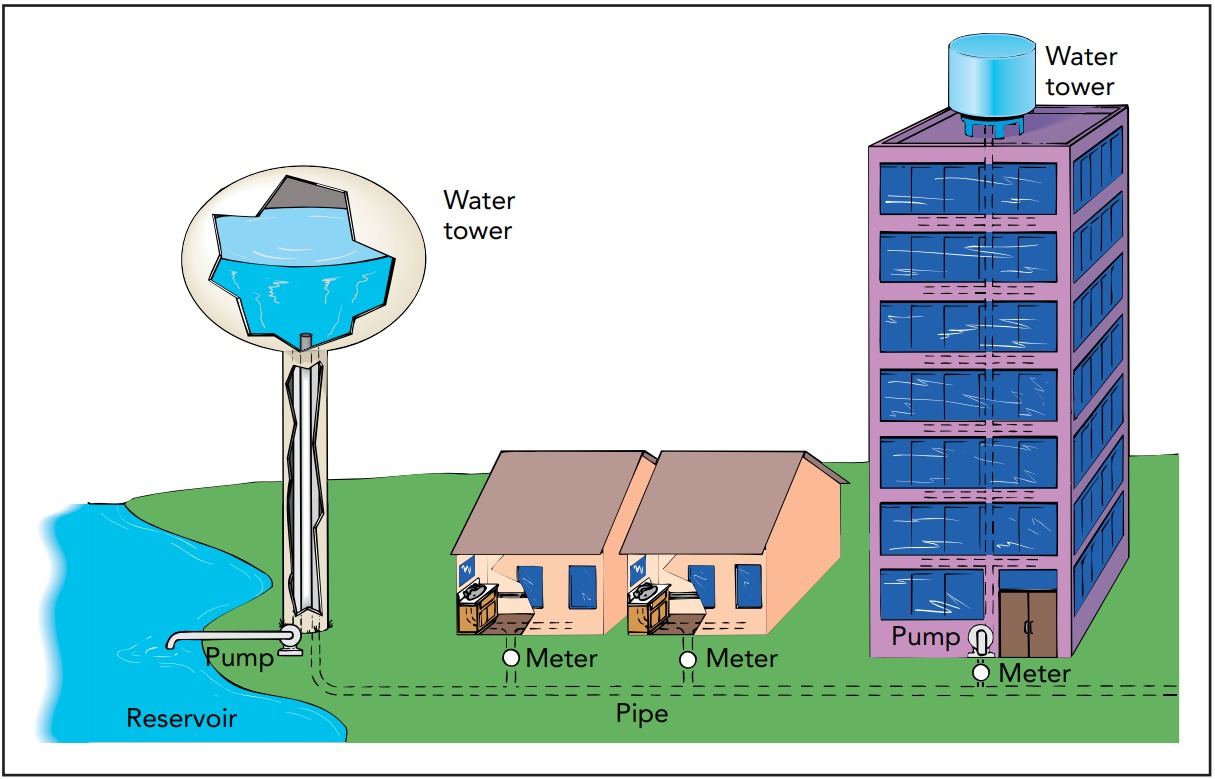
Water Pressure
Water distribution systems require two things: plumbing and water pressure. Plumbing is what delivers the water, and water pressure is what starts that water flowing. Water pressure is important because, like everything else, water has mass and accelerates only when pushed. The pushes that send water through pipes come principally from differences in water pressure. Water accelerates only in response to unbalanced pressures. If the water pressure inside a pipe is uniform, then each portion of water feels no net force and doesn’t accelerate; it either remains stationary or coasts at constant velocity. If the pressure is out of balance, however, then each portion of water experiences a net force and accelerates toward the region of lowest pressure.
Because of its inertia, water changes velocity gradually; it speeds up, slows down, or turns to the side, depending on where the lowest pressure is located. A complicated arrangement of high and low pressures can steer water through an intricate maze of pipes, and that is exactly how water reaches your home from the city pumping station. Every change in its velocity during its trip through the plumbing is caused by a pressure imbalance.
Creating Water Pressure with Water Pumps
To start water flowing through the plumbing in a level house or city, you need a water pump, a device that uses mechanical work to deliver pressurized water through a pipe. At its most basic level, a water pump squeezes a portion of water to raise its local pressure so that it accelerates toward regions of lower pressure. The pump continues to squeeze that water as it flows out through the plumbing.
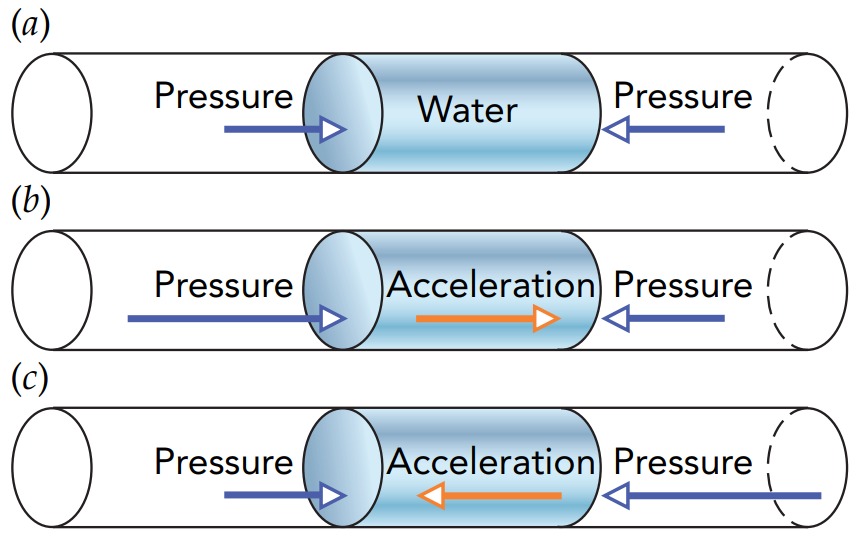
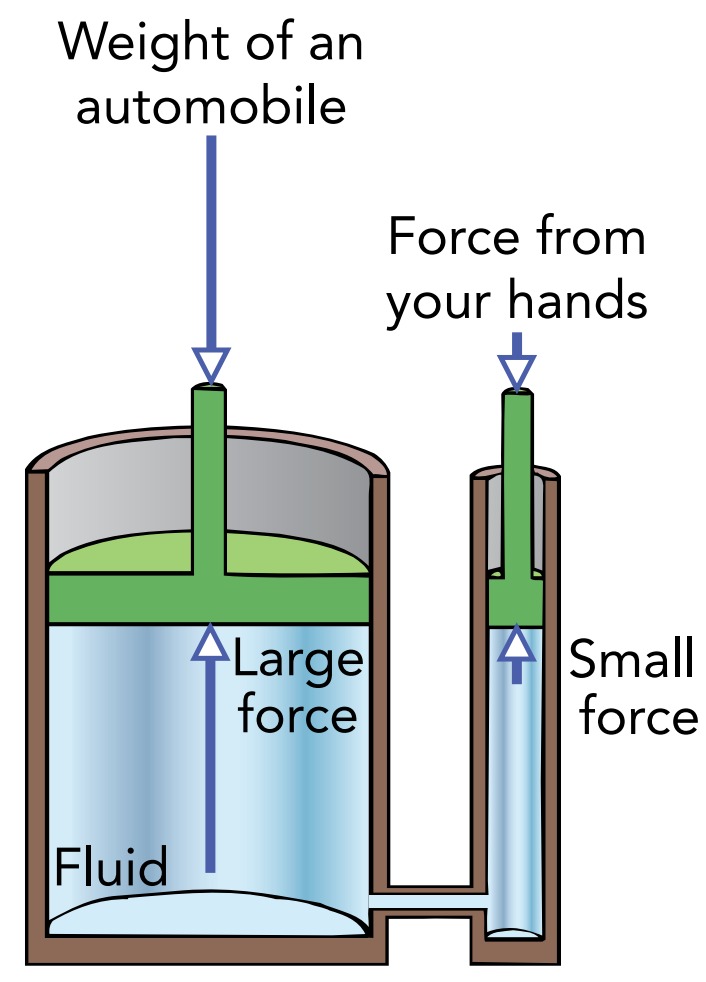
when you squeeze the sides of the bottle and push inward on the water, the water responds by pushing outward on you. The harder you push, the harder the water pushes back and the greater its pressure becomes. Water, like all liquids, is incompressible; that is, it experiences almost no change in volume as its pressure increases. The pressure increases uniformly throughout the water bottle, an observation known as Pascal’s principle: a change in the pressure of an enclosed incompressible fluid is conveyed undiminished to every part of the fluid and to the surfaces of its container. This uniform pressure rise leads to a large upward force. That effect is the basis for hydraulic systems and lifts, where pressure produced in an incompressible fluid by a small force exerted on a small area of the fluid’s container results in a large force exerted on a large area of the fluid’s container.
Now when you squeeze the bottle and increase the local water pressure, the water can move. As its pressure increases inside the bottle, the water begins to accelerate toward the lower pressure outside the bottle’s open top and the result is a fountain. You are pumping water! You are also doing work; as the water flows out of the bottle, your hands move inward. Since you are pushing inward on the water and the water is moving inward, you are doing work on the water. Pumps do work when they deliver pressurized water, and pressurized water carries with it the energy associated with that work. Although a water bottle can act as a pump briefly, it soon runs out of water.
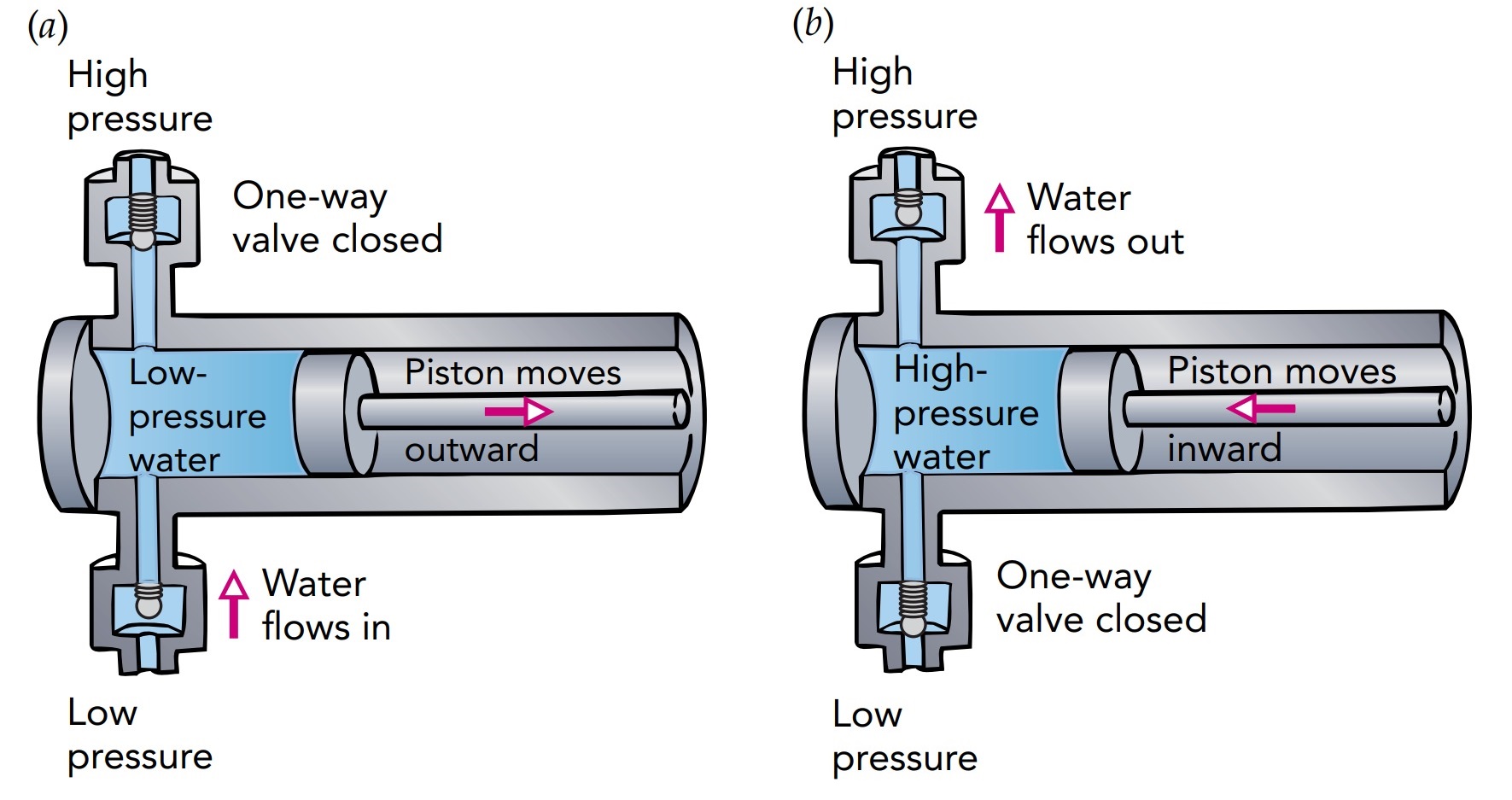
In a practical pump, a piston slides back and forth in the open end of a hollow cylinder, making a watertight seal. Pushing inward on that piston squeezes any water in the cylinder and increases the local water pressure. Water begins to flow. pump’s cylinder is easy to refill. The cylinder actually has two openings, each with a valve that permits water to flow in only one direction. Water can leave the cylinder only through the top opening and can enter only through the bottom opening. As you push the pump’s piston into the water-filled cylinder, the water pressure in the cylinder rises and water accelerates and flows out through the top valve. As you pull the pump’s piston out of the water-filled cylinder, the water pressure inside the cylinder drops and water accelerates and flows in through the bottom valve. In fact, as you withdraw the piston, the pressure inside the cylinder drops below atmospheric pressure, so even water in an open reservoir nearby will accelerate toward the partial vacuum in the cylinder and refill it.
Moving Water: Pressure and Energy
The pump can draw low-pressure water from a pond and fill a hose with high pressure water. If the nozzle at the other end of the hose is open, the water will accelerate toward lower pressure outside the nozzle and spray toward the garden with considerable kinetic energy.
The energy comes from you and the pump. As you push the piston into the cylinder, pressurizing the water and squeezing it out through the top valve, you’re doing work on the water—you’re exerting an inward force on the water, and the water is moving a distance in the direction of your force. The inward force you exert on the water is equal to the water pressure times the surface area of the piston, or
\[force = pressure · surface ~area, \]
and the distance the water moves is equal to the volume of water pumped divided by the surface area of the piston, or
\[distance = \frac{volume}{surface ~area}\]
Since work equals force times distance, the work you do pumping water is equal to the water pressure times the volume of water you pump, or
\[work = pressure \times volume.\]
As you pump high-pressure water through the hose, high-speed water sprays out of its nozzle. Since water is incompressible, water enters and exits the hose at equal rates and the work you do pumping 1 liter of water into the hose becomes kinetic energy in 1 liter of water leaving the nozzle. That energy travels directly from the pump to the nozzle, and the water doesn’t actually store any of it along the way.
In steady-state flow, a fluid flows continuously and steadily through a stationary environment. When you watch steady-state flow, you can’t detect the passage of time in either the fluid or its environment, and a video of steady-state flow looks exactly like a still photograph. With small allowances for the inevitable imperfections of real life, water traveling steadily through the plumbing in your home, a soft wind blowing smoothly across your motionless cheek, and a gentle current flowing silently between the motionless banks of a lazy river are all cases of steady-state flow in fluids. The beauty of steady-state flow is in how it handles energy along streamlines. A streamline is the path taken by a tiny portion of water in the flow. In steady-state flow, an endless series of identical drops travels that same unchanging streamline. In steady-state flow with no friction-like effects, a drop’s ordered energy remains constant as it travels along its streamline. Moreover, since all the drops along that streamline are identical, the ordered energy per drop is constant everywhere along that streamline.
According to the Bernoulii's equation, after Swiss mathematician Daniel Bernoulli,
\[\frac{ordered ~energy}{volume} = \frac{pressure~ potential~ energy}{volume} + \frac{kinetic ~energy}{volume} .\]
\[\frac{ordered ~energy}{volume} = pressure + \frac{1}{2} · density · speed^{2} = constant~ (along ~a ~streamline).\]
It applies only to incompressible fluids such as water and assumes no ordered energy is wasted by friction-like effects. water that’s in steady-state flow can exchange pressure for speed or speed for pressure as it flows along a streamline. As water accelerates out of a nozzle, for example, its pressure drops but its speed increases because it’s converting pressure potential energy into kinetic energy. And as that moving water sprays against the car you’re washing, it slows down but its pressure increases because it’s converting kinetic energy back into pressure potential energy. In both cases, the water’s ordered energy is constant.
Gravity and Water Pressure
Gravity creates a downward pressure gradient in water; the deeper the water, the more weight there is overhead and the greater the pressure. Since water is much denser than air, water pressure increases rapidly with depth. In a vertical pipe that’s open on top, the water’s surface is at atmospheric pressure (about 100,000 Pa). Only 10 m (33 feet) below the water’s surface, however, the pressure has already doubled to 200,000 Pa. At that modest depth, the water overhead weighs as much as the air overhead, even though the atmosphere is many kilometers thick.
The shape of the pipe doesn’t affect the relationship between pressure and depth. No matter how complicated the plumbing, the pressure of stationary water inside it increases with depth by 10,000 Pa per meter, or 10,000 Pa/m. This uniform downward pressure gradient creates an upward buoyant force on anything immersed in the water. In fact, that buoyant force is what supports the water itself.
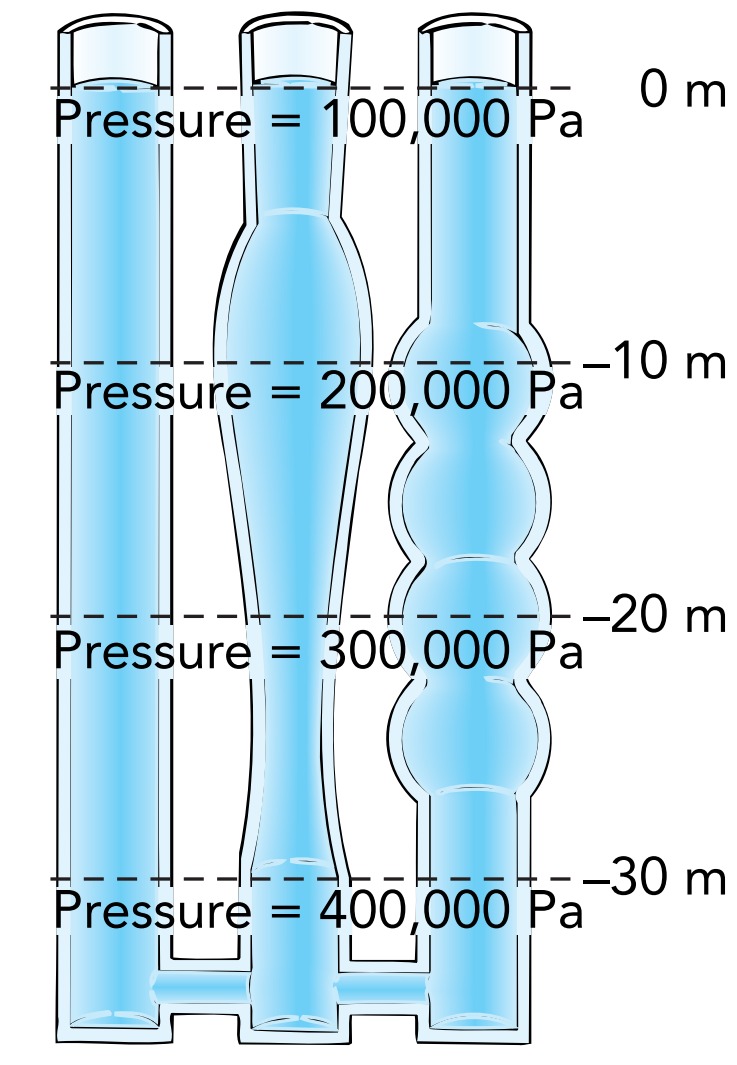
The dependence of water pressure on depth has a number of important implications for water distribution.
First, water pressure at the bottom of a tall pipe is substantially higher than at the top of that same pipe. Consequently, if only a single pipe supplies water to a skyscraper, then the water pressure on the ground floor will be dangerously high while the pressure in the penthouse will be barely enough for a decent shower. Tall buildings must therefore handle water pressure very carefully; they can’t simply supply water to every floor directly from the same pipe.
Second, pressure in a city water main does more than just accelerate water out of a showerhead; it also supports water in the pipes of multistory buildings. Lifting water to the third floor against the downward force of gravity requires a large upward force, and that force is provided by water pressure. The higher you want to lift the water, the more water pressure you need at the bottom of the plumbing. Lifting the water also requires energy, which is often provided by a water pump.
Third, as water travels up and down the streets of a hilly city, its pressure varies with height. In the valleys the pressure can be very large, and at the tops of hills the pressure can be very small. Water mains in valleys must therefore be particularly strong to keep from bursting. The large pressure in a valley is quite useful because it helps push the water back uphill on the other side of the valley. A hilly city must have pumping stations and other water-pressure-control systems located throughout to provide reasonable water pressures to all the buildings, regardless of their altitudes. Apart from those pressure-control systems, even a hilly city’s plumbing often involves steady-state flow and can be explained using a version of Bernoulli’s equation that includes gravity.
When all of those free surfaces are at atmospheric pressure, there are no pressure imbalances and the water accelerates only in response to gravity. The water’s only potential energy is gravitational and, like any object, it accelerates in the direction that lowers that gravitational potential as quickly as possible. If the water’s free surface is higher in one place than another, it can reduce its average height and, therefore, its gravitational potential energy by letting its highest water fill in its lowest valley. After some sloshing about, the water settles down in stable equilibrium with all its free surfaces smooth and level at a single uniform height. No matter how complicated the plumbing, water that is open to the air on top always “seeks its level.” The natural flow associated with this leveling effect is often used in water delivery
Remarkably, the leveling effect works even when some of the water-filled plumbing is located above the water’s free surfaces. For example, water can seek its level between two open containers through an elevated pipe known as a siphon. In such cases, the pressure of water in those elevated segments of plumbing is less than atmospheric pressure. If you seal off part of the isolated plumbing and reduce the pressure above one of the water’s free surfaces, that surface will rise higher than all of the others. It will rise until the added pressure produced by the taller column of water replaces the missing pressure above the water’s free surface. The less pressure there is above that surface, the higher the water must rise to make up for the missing pressure. This effect lifts water in a drinking straw and allows it to travel between two open containers in a siphon.
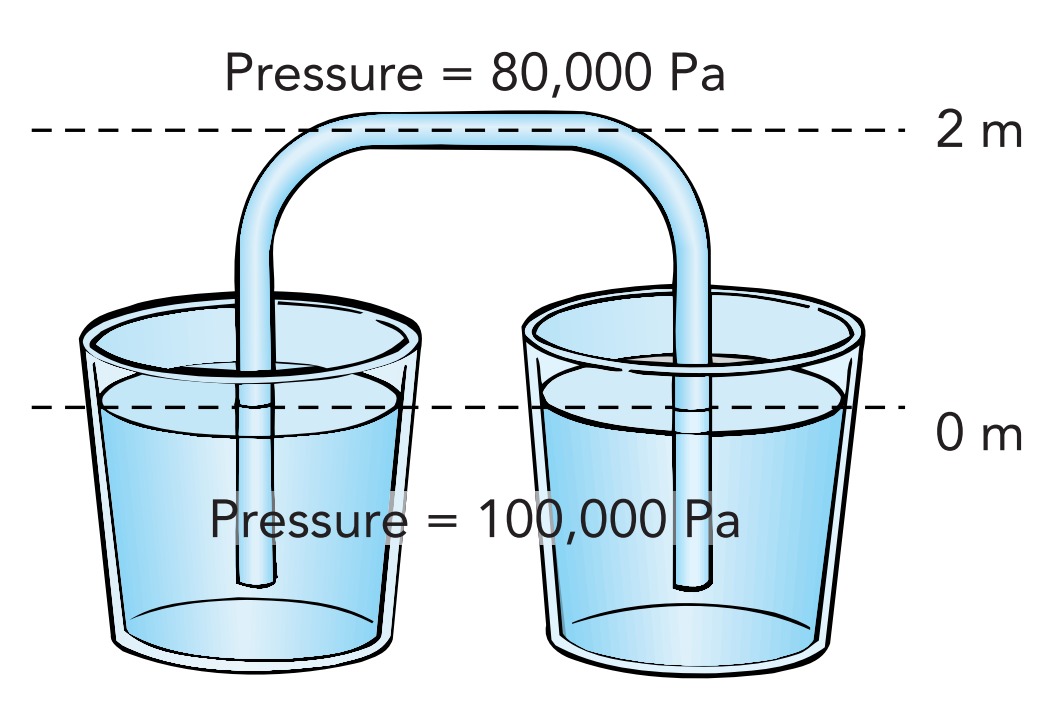
However, removing all the air pressure above the water’s free surface inside a long straw or siphon will raise its height only about 10 m (33 feet) above the level of the water elsewhere in an open container. Even with no pressure above it, this 10 m column of elevated water completely replaces the absent air pressure and thus prevents water in the rest of the plumbing from lifting it any higher. It’s therefore impossible to draw water from a deep well simply by lowering a pipe into that well and reducing the air pressure in the pipe; the water will rise no more than 10 m upward. Instead, a pump must be attached to the bottom of the pipe to pressurize the water and push it all the way to the top of the pipe.
Moving Water Again: Gravity
A drop’s gravitational potential energy is mass times the acceleration due to gravity times its height. The water’s gravitational potential energy per volume is thus its density times the acceleration due to gravity times its height. If we include gravitational potential energy, for fluids in steady-state flow along a streamline, the energy per volume is constant, we obtain a relationship that can be written as a word equation:
\[\frac{ordered ~energy} {volume} = \frac{pressure~ potential ~energy}{volume}+ \frac{kinetic~ energy}{volume}+\frac{gravitational ~potential~ energy}{volume}\]
\[ = pressure + \frac{1}{2} · density · speed^{2} + density · acceleration~ due ~to~ gravity · height \]
\[ = constant~ (along~ a ~streamline)\]
in symbols:
\[E/V = p + \frac{1}{2} · ρ · v^{2} + h · ρ · g = constant (along a streamline)\]
and in everyday language:
When a stream of water speeds up in a nozzle or flows uphill in a pipe, its pressure drops
This is a revised version of Bernoulli’s equation, one that includes gravity. It correctly describes steady-state flow in streamlines that change height. As before, it applies only to incompressible fluids such as water and assumes no ordered energy is wasted by friction-like effects.
Because energy is conserved, water that’s in steady-state flow can exchange the energies associated with its speed, pressure, and height for one another. Thus as water flows downward, its speed or pressure or both increase; if it falls from an open faucet, its speed increases; and if it descends steadily inside a uniform pipe, its pressure increases. The reverse happens as water flows upward. Water rising from a fountain loses speed as it ascends, while water rising steadily in a uniform pipe loses pressure on its way up.
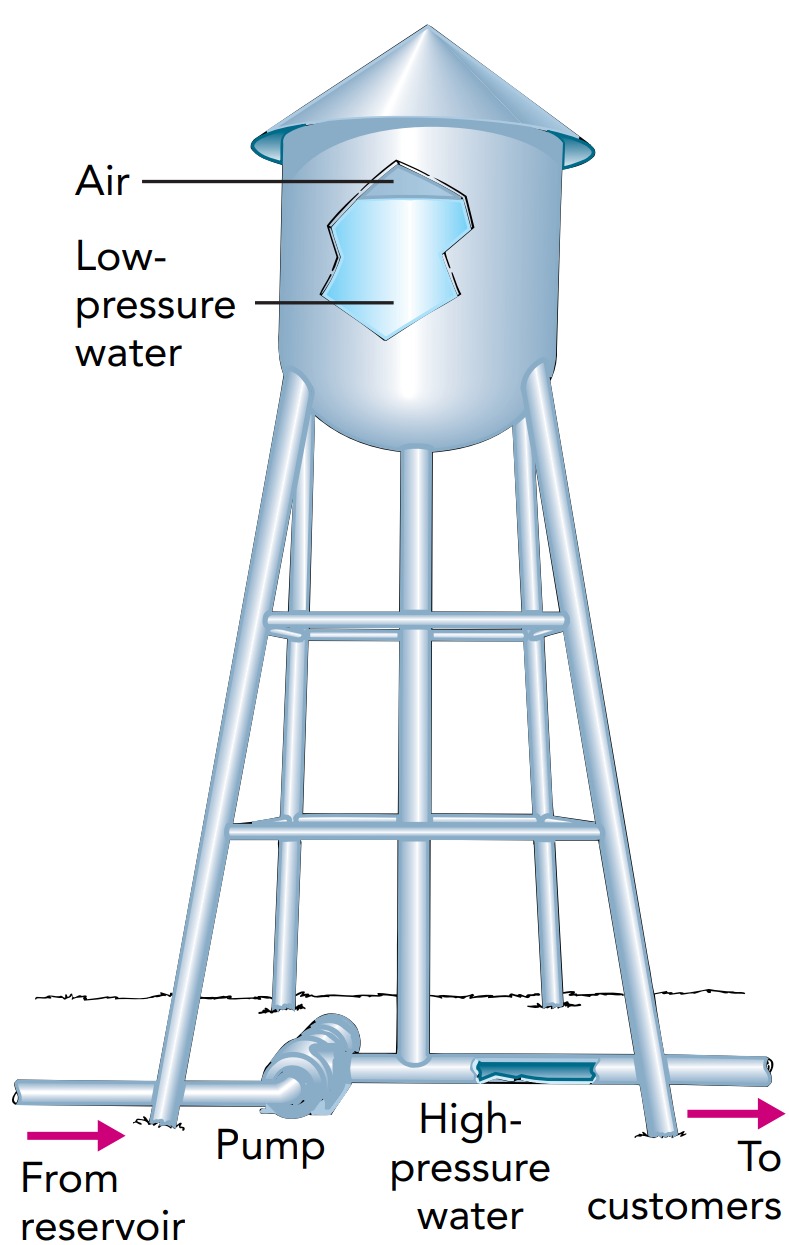
This interchangeability of height, pressure, and speed makes it possible to pressurize plumbing by connecting a tall column of water to the pipes. That’s why cities, communities, and even individual buildings have water towers. A water tower is built at a relatively high site within the region it serves. A pump fills the water tower with water, and then gravity maintains a constant high pressure throughout the plumbing that connects to it. The water is at atmospheric pressure at the top of the water tower, but the pressure is much higher at the bottom; at the base of a 50-m-high water tower, for example, the pressure is about 600,000 Pa, or six times atmospheric pressure.
In addition to providing a fairly steady pressure in the water mains, a water tower stores energy efficiently and can deliver that energy quickly. When water is drawn out of the water tower, its gravitational potential energy at the top becomes pressure potential energy at the bottom. The water tower replaces a pump, supplying a steady flow of water at an almost constant high pressure. Unlike a pump, however, the water tower can supply this high-pressure water at an enormous rate. As long as the water level doesn’t drop too far, high-pressure water keeps flowing.