Fluids are fascinating when they move. Stationary water and air may be essential to life, but they’re also fairly simple; only their pressures vary from place to place, and even these are determined primarily by gravity. Rushing rivers or gusts of wind, however, with their wonderful variety of simple and complicated behaviors, are much more exciting. The motions of fluids aren’t just interesting; they’re also important, since our world is filled with objects and machines that work in whole or part because of the behaviors of moving fluids.
Garden Watering
Tending a flower garden often involves watering. While this once meant walking the garden’s paths with a watering can, modern plumbing has made such effort unnecessary. With a hose and nozzle attached to a faucet, you can do your job without leaving your lawn chair. Although the tools involved—faucets, hoses, and nozzles—are simple and unsophisticated, the principles behind them are not. All three make elegant use of the laws of fluid flow and will introduce us to several important complications, notably friction-like effects and turbulence.
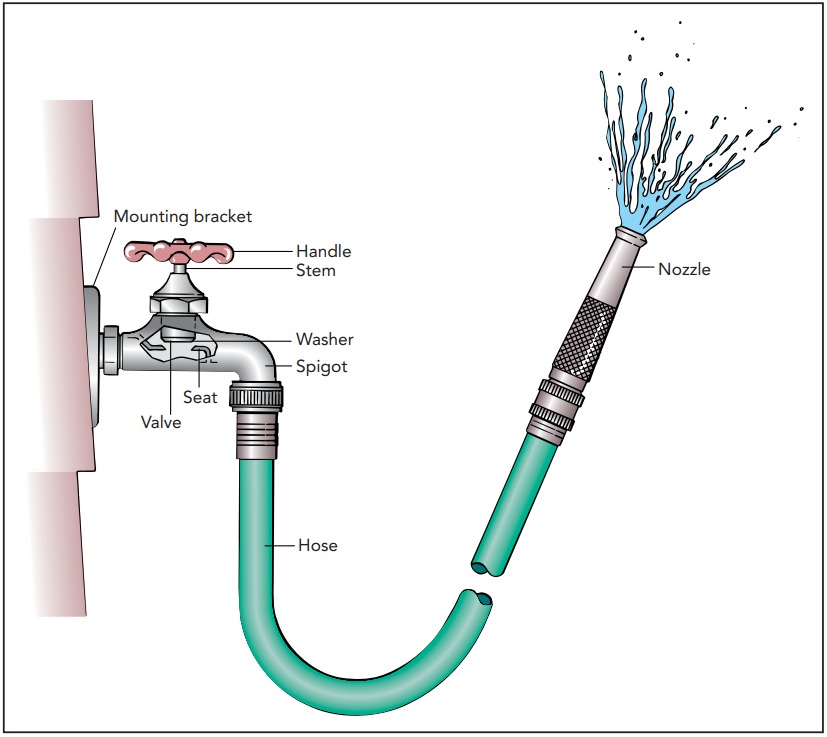
Water’s Viscosity
Having brought water to your home well on our way to watering your garden. However, to reach the garden, water must first travel through a long stretch of hose that’s lying straight on level ground. Does the length of this hose have any effect on the water delivery process?
The answer is yes, longer hoses generally deliver less water. Moving water doesn’t slide freely through a stationary hose. In reality, it experiences frictional forces that oppose its motion relative to the hose. This friction is unusual, though, because most of the water in the hose never actually touches the hose itself. If water deep inside the hose is going to experience any forces due to relative motion, then those forces are going to have to occur within the water. Water must exert frictional forces on itself!
Water does experience internal frictional forces. They’re called viscous forces, forces that appear whenever one layer of a fluid tries to slide across another layer of that fluid. Viscous forces oppose relative motion, and you can observe their effects easily when you pour honey out of a jar. The honey at the jar’s surface is stuck there by chemical forces and remains stationary. But even honey that’s far from the walls can’t move easily; it experiences viscous forces as it tries to move relative to nearby honey. Since honey is a “thick,” or viscous, fluid, viscous forces act quite effectively to keep all the honey moving with nearly the same velocity. Since the honey at the walls can’t move, viscous forces tend to prevent any of the honey from moving.
The measure of this resistance to relative motion within a fluid is called viscosity, and water’s viscosity is less than that of honey. In fact, if you heat the water up, it will become even less viscous and thus flow more easily. Typical of most liquids, this decrease in viscosity with increasing temperature reflects the molecular origins of viscous forces: the molecules in a liquid stick to one another, forming weak chemical bonds that require energy to break. In a hot liquid, the molecules have more thermal energy, so they break these bonds more easily to move past one another.
Flow in a Straight Hose: The Effect of Viscosity
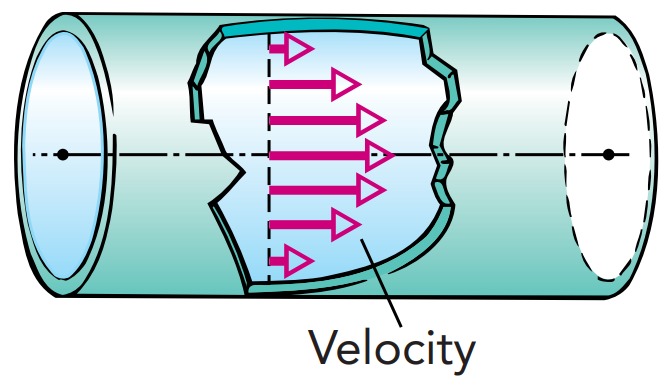
Viscosity slows the flow of water through your hose. Chemical forces between the hose and the outermost layer of water hold that layer of water stationary, and this motionless layer exerts viscous forces on the layer of moving water inside it. As this second layer slows, it exerts viscous forces on yet another layer. Layer by layer, viscous forces hold back the moving water until even water at the center of the hose feels viscosity’s slowing effects. Although water at the center of the hose moves faster than water in any other layer, it’s still affected by the stationary hose.
These viscous forces impede water delivery. Instead of coasting effortlessly through the straight, level hose, real water needs a pressure gradient to push it steadily forward. Water must be pushed through the hose if it’s to maintain a continuous flow. Also, the water becomes hotter as the work done pushing it forward is wasted and becomes thermal energy.
viscous forces become larger as the relative velocities within a fluid increase. That’s because as two layers of water slide past one another faster, their molecules collide harder and more frequently. Since it experiences stronger viscous forces, fast-moving water wastes more energy per meter and needs a larger pressure gradient to keep it moving steadily through a hose than does slow-moving water. Because of viscous forces, the amount of water flowing steadily through a hose has four properties:
- It’s inversely proportional to the water’s viscosity. The more viscous the water, the more difficulty it has flowing through the hose.
- It’s inversely proportional to the length of the hose. The longer the hose, the more opportunity viscous forces have to slow the water down.
- It’s proportional to the pressure difference between the hose’s inlet and its outlet. This pressure difference determines the water’s pressure gradient and thus how hard the water is pushed forward through the hose.
- It’s proportional to the fourth power of the diameter of the hose. Tripling the hose’s diameter provides the water with nine times as much room and also allows water near the hose’s center to move nine times faster.
POISEUILLE’S LAW
The volume of fluid flowing through a cylindrical pipe each second is equal to (𝜋/128) times the pressure difference (Δp) across that pipe times the pipe’s diameter to the fourth power, divided by the pipe’s length times the fluid’s viscosity (ƞ).
We can turn these four proportional relationships into an equation by adding the correct numerical constant (π/128). The final relationship is called Poiseuille’s law and can be written as a word equation:
\[volume~flow = \frac{\pi · pressure~ difference · pipe ~diameter^{4}} {128 · pipe~ length · fluid ~viscosity}\]
The speed of water flowing through a pipe is not constant across the pipe. The water near the walls is stationary, while the water at the center of the pipe moves the fastest. The differences in velocity are the result of viscous forces.
in symbols:
\[\frac{\Delta V}{\Delta t} = \frac{\pi · \delta p · D^{4}}{128 · L · \eta}\] and in everyday language:
It’s hard to squeeze honey through a long, thin tube.
By opposing the flow of water through a hose, viscous forces do negative work on it and reduce its ordered energy— the energy considered in Bernoulli’s equation, which doesn’t include thermal energy. Just how much ordered energy the water retains depends on how fast it moves inside the hose. If you allow lots of water to leave the hose, water will move through it quickly and encounter large viscous forces. In the process, most of the water’s ordered energy will be wasted as thermal energy and the water will pour gently out of the end of the hose. However, if you partially block the hose’s opening with your thumb and reduce the flow, water will travel slowly through the hose and encounter smaller viscous forces. As a result, the water will retain most of its ordered energy and will still be at high pressure when it reaches your thumb. This high-pressure water will then accelerate to enormous speed as it passes through the narrow opening and sprays out into the air.
Hence, water delivery systems normally use the widest pipes that are practical and affordable. In contrast to a narrow hose, wide pipes can carry large amounts of water while letting that water travel slowly, experience weak viscous forces, and waste little of its ordered energy. In such energy-efficient water delivery systems, friction is insignificant and Bernoulli’s equation accurately predicts water’s properties throughout its trip.
Flow in a Bent Hose: Dynamic Pressure Variations
The hose bends toward the right on reaching the garden hose and the flowing water bends with it. That water is accelerating as it turns. water accelerates horizontally only in response to unbalanced pressures. Since the hose is motionless, the unbalanced pressures inside it must be caused by the water itself; the water is experiencing dynamic pressure variations.
To understand these dynamic pressure variations, let’s follow the streamlines as water traverses this bend. Viscous forces are certainly important in the long narrow hose; however, the bend is so short that viscous forces have little effect on what happens to the water passing through it.
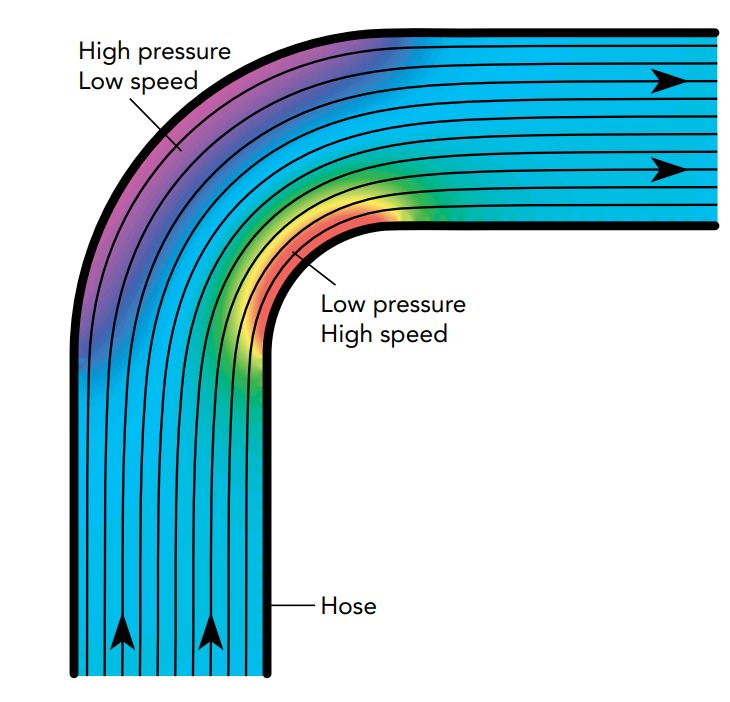
Neglecting viscous forces, the water’s ordered energy is constant along each streamline and we can observe the interchanges of energy allowed by Bernoulli’s equation. However, since the hose rests on level ground, water’s gravitational potential energy can’t vary and the only interchanges we’ll see are between pressure potential energy and kinetic energy.
Figure shows the water’s steady-state flow pattern near the bend. We’re looking down on the hose in this calculated drawing and, as indicated by the black streamlines, water that is initially flowing straight ahead arcs rightward at the bend and eventually continues directly toward the right.
Water approaches the bend through a straight section of hose in which its streamlines are straight and parallel. Water flows at constant velocity along these streamlines—the water’s direction is fixed and it can’t change its speed. If it tried to speed up, it would leave a gap behind it; if it tried to slow down, it would cause a “traffic jam.” The water’s pressure must be uniform throughout this straight section because it would accelerate if there were any differences in pressure.
The water’s constant velocity and uniform pressure are represented visually in Fig. Local water velocities are revealed by the directions and separations of the streamlines. Water’s velocity always points along its streamline, and its speed is inversely proportional to the streamline spacing. Streamlines that become more widely spaced denote decreasing speed—water that slows down spreads out sideways and its streamlines separate from one another. Streamlines that become more narrowly spaced denote increasing speed—water that speeds up stretches out along its path and its streamlines draw toward one another. Since the streamlines leading up to the bend are straight and evenly spaced, we know that water moves along each streamline at constant velocity.
Local water pressure is displayed in Fig. as the colors of the rainbow. Colors toward the violet end of the spectrum denote higher pressures, while those toward the red end of the spectrum denote lower pressures. Since the straight section has a uniform bluegreen color, the water there has a uniform, moderate pressure.
Once the water starts bending toward the right, however, its velocities and pressures begin to vary. Since the water is accelerating toward the inside of the bend, there must be a pressure imbalance pushing it in that direction. Sure enough, the turning stream of water develops higher local pressure (violet) near the outside of the bend and lower local pressure near the inside of the bend (red). A similar pressure imbalance accompanies any bend in a fluid’s path; the pressure is always higher on the outside of the bend than it is on the inside of that bend. After all, that pressure imbalance is what causes the fluid flow to bend!
To keep the ordered energy constant along a streamline, each decrease in the water’s local pressure is accompanied by an increase in the water’s local speed, and the opposite is also true. Water arcing around the outside of the bend slows down (the streamline spacing widens) as its pressure rises, while the water arcing around the inside of the bend speeds up (the streamline spacing narrows) as its pressure drops.
As the hose straightens out beyond the bend, the water’s pressures and speeds return to what they were before the bend. Water from the outside of the bend speeds up and its pressure drops, while water from the inside of the bend slows down and its pressure rises. In the straight section following the bend, water’s velocity is once again constant along each streamline and its pressure is uniform.
You might wonder which causes which: Does each pressure change cause a speed change, or does each speed change cause a pressure change? The answer is that they occur together and are equally entitled to be called cause and effect. Once the steady-state flow pattern has established itself, water following a particular streamline experiences rises and falls in pressure at the same time that it experiences decreases and increases in speed. The two effects—pressure changes and speed changes—simply go hand in hand.
Flow through a Nozzle: From Pressure to Speed
When water finally flows through the nozzle at the end of your hose, it exchanges its remaining pressure potential energy for kinetic energy and sprays out into the garden. The nozzle’s narrowing channel initiates this energy transformation so that low-speed, high-pressure water entering the nozzle becomes fast-moving, atmospheric-pressure water leaving the nozzle.
Figure shows that, as water passes through the nozzle, the narrowing channel herds all the streamlines together, so the water’s local speed increases. The water following each streamline is speeding up to squirt through the bottleneck without causing a backup. This increase in water’s local speed is accompanied by a decrease in water’s local pressure, as indicated by the color shift toward the red end of the spectrum.
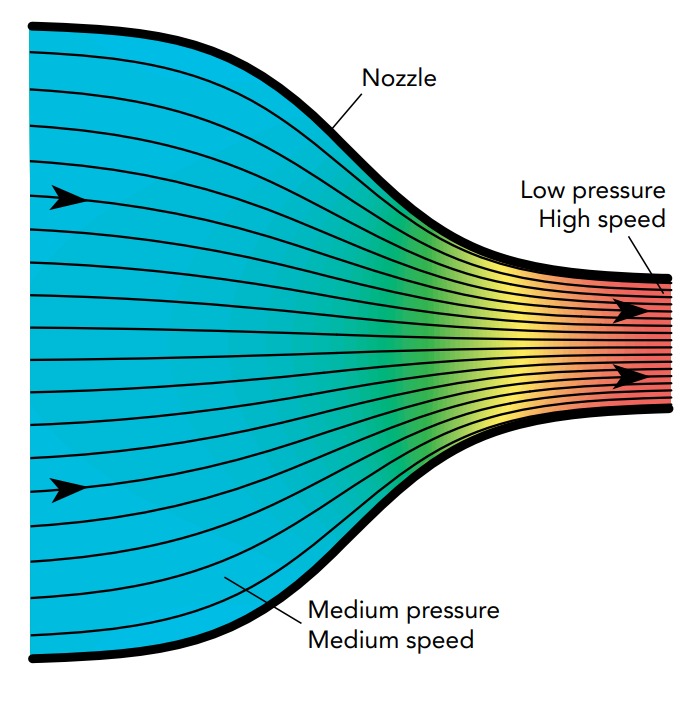
By the time the water leaves the hose nozzle, its pressure has dropped all the way to atmospheric pressure and it has turned all its available pressure potential energy into kinetic energy. It emerges as a narrow stream of fast-moving water and arcs gracefully through the air. No wonder you can reach the farthest parts of your garden with water when you use a nozzle
The Onset of Turbulence
As you direct the stream of water at the plants in your garden, you notice two interesting phenomena: first, the stream pushes on any surface that slows it down, and second, it tends to break up into fragments as it flows around obstacles. The pushing effect is another Bernoulli result: when the stream collides with a surface and bends away, its pressure at the surface rises to cause the bend and that rising pressure pushes the surface forward.

The breakup effect, however, is something new. In trying to go around the obstacle, the stream of water loses its orderly structure and disintegrates into a swirling, hissing froth. Actually, the hiss you hear is familiar; you heard it as you opened the faucet to start water flowing through the hose. That faucet uses a movable stopper to control the flow of water into the hose; as you opened the faucet, you gradually removed this stopper from the water pipe to allow water to flow more freely into the hose and the faucet hissed. Whether water encounters a plant or a faucet stopper, there is something about high speeds and obstacles that upsets the smoothly flowing fluid.
Up until now, we’ve discussed only laminar flow, the smooth, silent flow that’s characterized by simple streamlines. In laminar flow, adjacent regions of a fluid always remain adjacent. For example, if you place two drops of dye near one another in a smoothly flowing stream, they will remain close together indefinitely as they follow streamlines in the laminar flow (Fig., left). Laminar flow is the orderly result of viscous forces, which tend to bring adjacent portions of fluid to the same velocity. When viscosity dominates a fluid’s motion, the flow is usually laminar.


However, as the stream flows swiftly past rocks and obstacles, its streamlines break up into the eddies and churning “white water” that make rafting exciting (Fig., right). The dye is quickly dispersed in this frenzied turbulence. The stream is experiencing turbulent flow, a roiling, noisy flow in which adjacent regions of fluid soon become separated from one another as they move independently in unpredictable directions. Turbulent flow is the disorderly consequence of inertia, which tends to propel each portion of fluid independently according to its own momentum. When inertia dominates a fluid’s motion, the flow is usually turbulent.
The plants and faucet stopper are evidently initiating turbulence in what had been laminar flows; flows that were dominated by viscous forces are suddenly dominated by inertia instead. Whether a flow is laminar or turbulent depends on several characteristics of the fluid and its environment:
- The fluid’s viscosity. Viscous forces tend to keep nearby regions of fluid moving together, so high viscosity favors laminar flow (Fig.).
- The fluid’s speed past a stationary obstacle. The faster the fluid is moving, the more quickly two nearby regions of fluid can become separated and the harder it is for viscous forces to keep them together.
- The size of the obstacle the fluid encounters. The larger the obstacle, the more likely that it will cause turbulence because viscous forces will be unable to keep the fluid ordered over such a long distance.
- The fluid’s density. The denser the fluid, the less it responds to viscous forces and the more likely it is to become turbulent.
Rather than keeping track of all four physical quantities independently, English mathematician and engineer Osborne Reynolds (1842–1912) found that they could be combined into a single number that permits a comparison of seemingly different flows. The Reynolds number is defined as
\[ Reynolds~ number = \frac{density · obstacle~ length · flow~ speed}{viscosity}\] .
The units on the right side of Eq. cancel one another, so the Reynolds number is dimensionless; that is, it’s just a simple number, such as 10 or 25,000. As the Reynolds number increases, the flow goes from viscous-dominated to inertia-dominated and therefore from laminar to turbulent. In his experiments, Reynolds found that turbulence usually appears when the Reynolds number exceeds roughly 2300. You can observe this transition by moving a 1-cm-thick stick through still water. If you move the stick slowly, about 10 cm/s, the Reynolds number will be about 1000 and the flow around the stick will be laminar. But if you speed the stick up to about 50 cm/s (20 in/s), the Reynolds number will rise to about 5000 and the flow will become turbulent.
One of the most common features of turbulent flows is the vortex, a swirling region of fluid that moves in a circle around a central cavity. A vortex resembles a miniature tornado, with its cavity created by inertia as the fluid spins. Vortices are easily visible behind a canoe paddle, in a mixing bowl, or in a cup of coffee stirred rapidly with a spoon. Once an object moves fast enough through a fluid to create turbulence, these vortices begin to form. Each vortex builds up behind the object but is soon whisked away to form a wake of shed vortices, vortices that have broken free of the object that made them.
While laminar flow is fully predictable, turbulent flow exhibits chaotic behavior or chaos; you can no longer predict exactly where any particular drop of water will go. The study of chaos is a relatively new field of science. Because a chaotic system, that is, a system exhibiting chaos, is exquisitely sensitive to initial conditions, even the slightest change in those conditions may produce profound changes in its situation later on.
The churning motion of turbulence converts some of the water’s ordered energy into thermal energy and sound. The turbulence near the faucet slightly reduces the water’s ordered energy as it enters the hose and therefore its speed as it emerges from the nozzle and sprays toward your garden.
A different sound occurs when you abruptly close the nozzle and stop the flow of water. Moving water has momentum, and stopping it suddenly requires an enormous backward force. Since the slowing flow is not steady state, Bernoulli’s equation doesn’t apply and the pressure can surge to astronomical values near the front of the moving water. This pressure surge is what accelerates the water backward to slow it down and what leads to the loud “thump” sound you hear as the water stops. Known as water hammer, the surging pressure in front of stopping water jerks the nozzle, swells the hose, and may even rattle the pipes in your home.