Air Sports
Much of the subtlety and nuance in games such as baseball and golf come from the way balls interact with air. If baseball were played on the moon, which has no air, the only pitches would be the fastball and the not-so-fastball. Moon golfers wouldn’t have to worry about hooks or slices.


When a Ball Moves Slowly: Laminar Airflow
One of the first things you might notice if you joined a new baseball franchise on the moon is that pitched balls reach home plate faster than back at home. Since the moon has no atmosphere, there is no air resistance to slow a ball down. In the previous section, we saw how objects affect moving fluids. Now as we study aerodynamics, the science of air’s dynamic interactions, we’ll see how fluids affect moving objects.
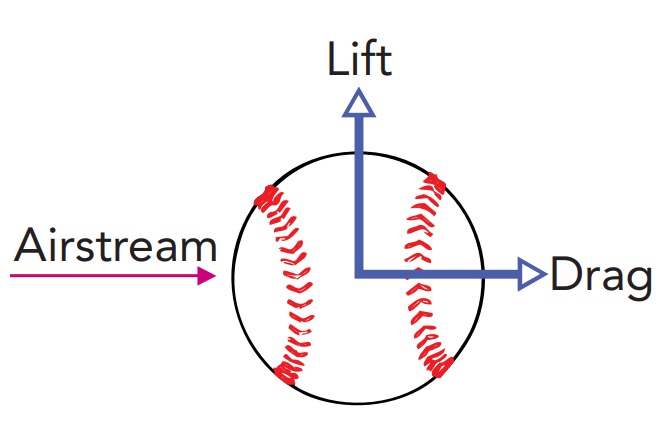
In air, a moving ball experiences aerodynamic forces—that is, forces exerted on it by the air because of their relative motion. These consist of drag forces that push the ball downwind and lift forces that push the ball to one side or the other (Fig.). We’ll begin our study of ball aerodynamics with drag forces, commonly called air resistance, and we’ll start with a slow-moving ball. The reason for starting slow is that at low speeds viscous forces are able to organize the air as it flows around the ball; viscosity dominates over inertia, and the airflow around the slow-moving ball is laminar.
The two types of aerodynamic forces exerted on objects by air are drag and lift. Drag is exerted parallel to the onrushing airstream and slows the object’s motion through the air. Lift is exerted perpendicular to that airstream so that it pushes the object to one side or the other. Lift is not necessarily in the upward direction.
Figure shows the pattern of laminar airflow around a slow-moving ball. Actually, the pattern is the same whether the ball moves slowly through the air or the air moves slowly past the ball. For simplicity, let’s move along with the ball and study the airflow from the ball’s inertial frame of reference. In that inertial frame, the ball appears stationary with the air flowing past it.
The slow-moving air separates neatly around the front of the ball and comes back together behind it. It produces a wake, an air trail behind the ball, that’s smooth and free of turbulence. However, the air’s speed and pressure aren’t uniform all the way around the ball. The airflow bends several times as it travels around the ball and, such bends always involve pressure imbalances. Since the air pressure far from the ball is steadfastly atmospheric, those pressure imbalances are always caused by pressure variations near the ball’s surface. Whenever air bends away from the ball, so that the ball is on the outside of a bend, the pressure near the ball must be higher than atmospheric. Whenever the air bends toward the ball, so that the ball is on the inside of a bend, the pressure near the ball must be lower than atmospheric.
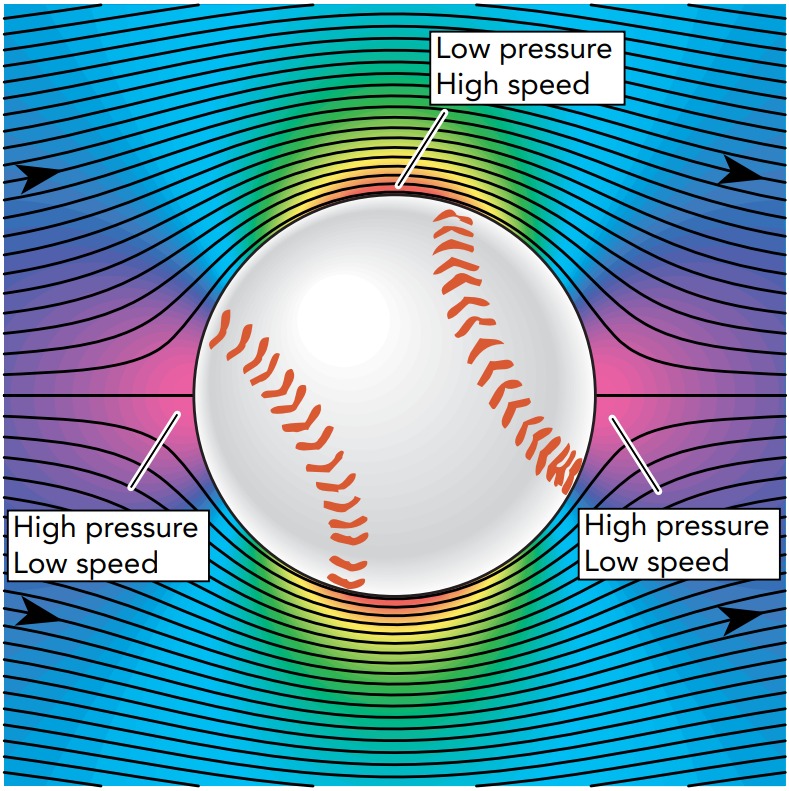
The airflow around a slowly moving ball is laminar. Air slows down in front of and behind the ball (widely spaced streamlines), and its pressure increases (shifts toward the violet end of the spectrum). Air speeds up at the sides of the ball (narrowly spaced streamlines), and its pressure decreases (shifts toward the red end of the spectrum). However, the pressure forces on the ball balance one another perfectly, and it experiences no pressure drag. Only viscous drag is present to affect the ball.
Air heading toward the ball’s front bends away from it, so the pressure near the front of the ball must be higher than atmospheric. This rise in air pressure is accompanied by a decrease in airspeed, the air’s speed relative to the ball. Figure indicates the pressure rise by a color shift toward the violet end of the spectrum and the decrease in airspeed by the widening separation of the streamlines. The air rounding the ball’s sides bends toward it, so the pressure near those sides of the ball must be below atmospheric. This drop in air pressure is accompanied by an increase in airspeed. Figure indicates the pressure drop by a color shift toward the red end of the spectrum and the increase in airspeed by the narrowing separation of the streamlines. The laminar airflow continues around to the back of the ball and then trails off behind it. Since the departing air again bends away from the ball, the pressure near the back of the ball must be higher than atmospheric. As before, the shift toward violet in Figure indicates this pressure rise and the widening separation of the streamlines points out the accompanying decrease in airspeed.
It may seem strange that the air pressure can be different at different points on the ball, but that’s what happens in a flowing stream of air. It’s particularly remarkable that lowpressure air at the sides of the ball is able to flow around to the back of the ball, where the pressure is higher. This air is experiencing a pressure imbalance that pushes it backward, opposite its direction of travel. But a pressure imbalance causes acceleration, not velocity, and the low-pressure air flowing past the sides of the ball has enough ordered energy and forward momentum to carry it all the way to the back of the ball. Although this air slows as it flows into the rising pressure, it manages to complete its journey. The airflow around the ball is symmetrical, and the forces that air pressure exerts on the ball are also symmetrical. These pressure forces cancel one another perfectly, so the ball experiences no overall force due to pressure. Most important, the high pressure in front of the ball is balanced by the high pressure behind it. As a result of this symmetrical arrangement, the only aerodynamic force acting on the ball is viscous drag, the downstream frictional force caused by layers of viscous air sliding across the ball’s surface
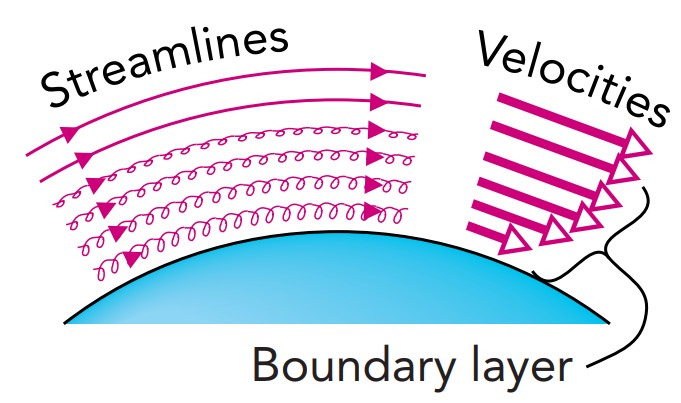
As air flows past a surface, a thin layer of it is slowed by viscous drag forces. This boundary layer is laminar at low Reynolds numbers and doesn’t become turbulent until the Reynolds number exceeds about 100,000.
When a Ball Moves Fast: Turbulent Airflow
Balls don’t always experience laminar airflow. Turbulence is common, particularly in sports, and brings with it a new type of drag force. When the air flowing around a ball is turbulent, the air pressure distribution is no longer symmetrical and the ball experiences pressure drag, the downstream force exerted by unbalanced pressures in the moving air. These unbalanced pressures exert an overall force on the ball that slows its motion through the air.
A ball can experience turbulent airflow and pressure drag when the Reynolds number exceeds about 2000. The Reynolds number, introduced in the previous section, combines the ball’s size and speed with the air’s density and viscosity to give an indication of whether the airflow is dominated by viscosity or inertia. At low Reynolds numbers, the air’s viscosity dominates over its inertia and the airflow is laminar. At high Reynolds numbers, however, air’s inertia dominates over its viscosity and the airflow tends to become turbulent. This turbulence, however, won’t start until something triggers it, and viscosity provides that trigger.
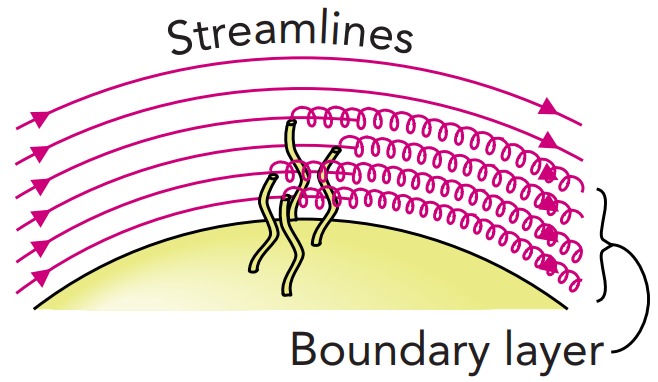
To understand viscosity’s role, we must look at the air near the ball’s surface. Even in a strong wind, viscous forces slow down a thin boundary layer of air near the ball’s surface (Fig.). Discovered by Ludwig Prandtl 5 with help from Gustave Eiffel (Fig.), this boundary layer moves more slowly and has less ordered energy than the freely flowing air farther from the surface. As air flows toward the back of the ball, it travels through an adverse pressure gradient, a region of rising pressure that pushes backward on the air and causes it to decelerate. While the freely flowing airstream outside the boundary layer has enough energy and forward momentum to continue onward and reach the back of the ball on its own, air in the boundary layer does not. It needs a forward push.

At low Reynolds numbers, the entire airstream helps to push that boundary layer all the way to the back of the ball and the airflow remains laminar. At high Reynolds numbers, however, viscous forces between the freely flowing airstream and the boundary layer are too weak to keep the boundary layer moving forward into the rising pressure behind the ball.
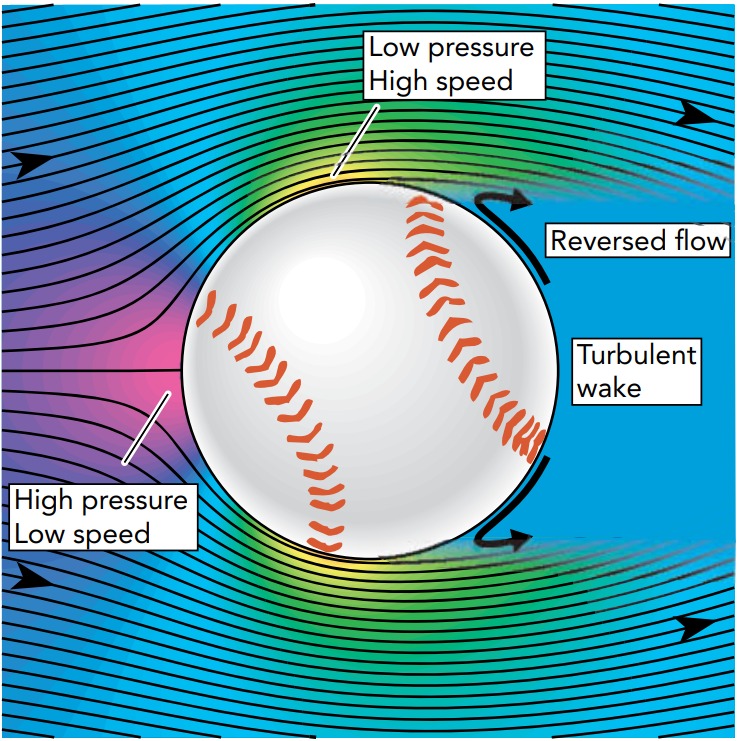
Without adequate help, the boundary layer eventually stalls; that is, it comes to a stop and thereby spoils steady-state flow. More horrible still, this stalled boundary layer air is pushed backward by the adverse pressure gradient and returns all the way to the ball’s sides. As it does, it cuts like a wedge between the ball and the freely flowing airstream. The result is an aerodynamic catastrophe—the airstream separates from the ball, leaving a huge turbulent wake or air pocket behind the ball (Fig.).
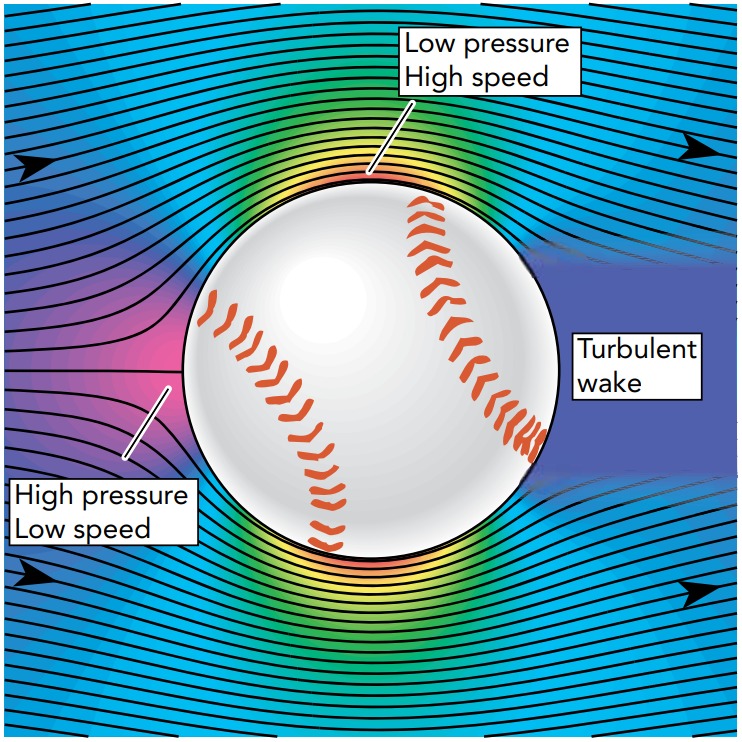
Because of this turbulent wake, air no longer bends smoothly away from the back of the ball and there is no rise in pressure there. Instead, the pressure behind the ball is roughly atmospheric. The absence of a high-pressure region behind the ball spoils the symmetry of pressure forces on the ball, and those forces no longer cancel. The ball experiences an overall pressure force downwind—the force of pressure drag. In effect, the ball is transferring forward momentum to the air in its turbulent wake and dragging that wake along with it.
Pressure drag slows the flight of almost any ball moving faster than a snail’s pace. The pressure drag force is roughly proportional to the cross-sectional area of the turbulent air pocket and to the square of the ball’s speed through the air. Area times speed is the volume of air the ball affects per second. The second factor of speed recognizes how much the air’s speed changes as the ball drags it along in its air pocket. For a ball moving at a moderate speed, the air pocket is about as wide as the ball and the ball experiences a large pressure drag force.
The Dimples on a Golf Ball
If this were the whole story, you would never hit a home run at a baseball game or a 250-yard drive on the golf course. But inertia has yet another card to play.
At very high Reynolds numbers, the boundary layer itself becomes turbulent (Fig.). It loses its laminar streamlines and begins to mix rapidly within itself and with the freely flowing airstream nearby. This mixing brings additional ordered energy and forward momentum into the boundary layer and makes it both harder to stop and more resistant to reversed flow. Although this turbulent boundary layer still stalls before reaching the back of the ball, the stalled air flows upstream only a short distance. The freely flowing airstream still separates from the ball; however, that separation occurs far back on the ball and the resulting turbulent wake is relatively small (Fig.).

As a result of this smaller air pocket, the pressure drag is reduced from what it would be without the turbulent boundary layer. The effect of replacing the laminar boundary layer with a turbulent one is enormous; it’s the difference between a golf drive of 70 yards and one of 250 yards!
Delaying the airflow separation behind the back of the ball is so important to distance and speed that the balls of some sports are designed to encourage a turbulent boundary layer (Fig.). Rather than waiting for the Reynolds number to exceed 100,000, the point near which the boundary layer spontaneously becomes turbulent, these balls “trip” the boundary layer deliberately (Fig.). They introduce some impediment to laminar flow that causes the air near the ball’s surface to tumble about and become turbulent. The drop in pressure drag more than makes up for the small increase in viscous drag, which is why a golf ball has dimples. A tennis ball’s fuzz, however, evidently creates more drag than it eliminates; shaving a tennis ball would actually help it maintain its speed.
The boundary layer can be made turbulent at Reynolds numbers below 100,000 by “tripping” it with obstacles such as fuzz or dimples.
Early golf balls were handmade of leather and stuffed with feathers. Golf became popular when cheap balls made of a hard rubber called gutta-percha became available. New, smooth “gutties” (top-left) didn’t travel very far, though; they flew better when they were nicked and worn. Manufacturers soon began to produce balls with various patterns of grooves (top-right) or bumps (bottom-left) on them, and those balls traveled dramatically farther than smooth ones. Modern golf balls (bottom-right) have dimples instead of grooves or bumps.
How much does drag affect balls in various sports? For those that involve rapid movements through air or water, the answer is quite a bit. Drag forces increase dramatically with speed; as soon as a turbulent wake and pressure drag appear, the drag force increases as the square of a ball’s speed. As a result, ball pitches slow significantly during their flights to home plate, and the faster they’re thrown, the more speed they lose. A 90-mph fastball loses about 8 mph en route, while a 70-mph curveball loses only about 6 mph.
Curveballs and Knuckleballs
The drag forces on a ball push it downstream, parallel to the onrushing air. In some cases, though, the ball may also experience lift forces—forces that are exerted perpendicular to the airflow (Fig.). To experience drag, the ball only has to slow the airflow down; to experience lift, the ball must deflect the airflow to one side or the other. Although its name implies an upward force, lift can also push the ball toward the side or even downward.
Curveballs and knuckleballs both use lift forces. In each of these pitches, the ball deflects the airstream toward one side and the ball accelerates toward the other. Again we have action and reaction—the air and the ball push off one another. Getting the air to push the ball sideways is no small trick.
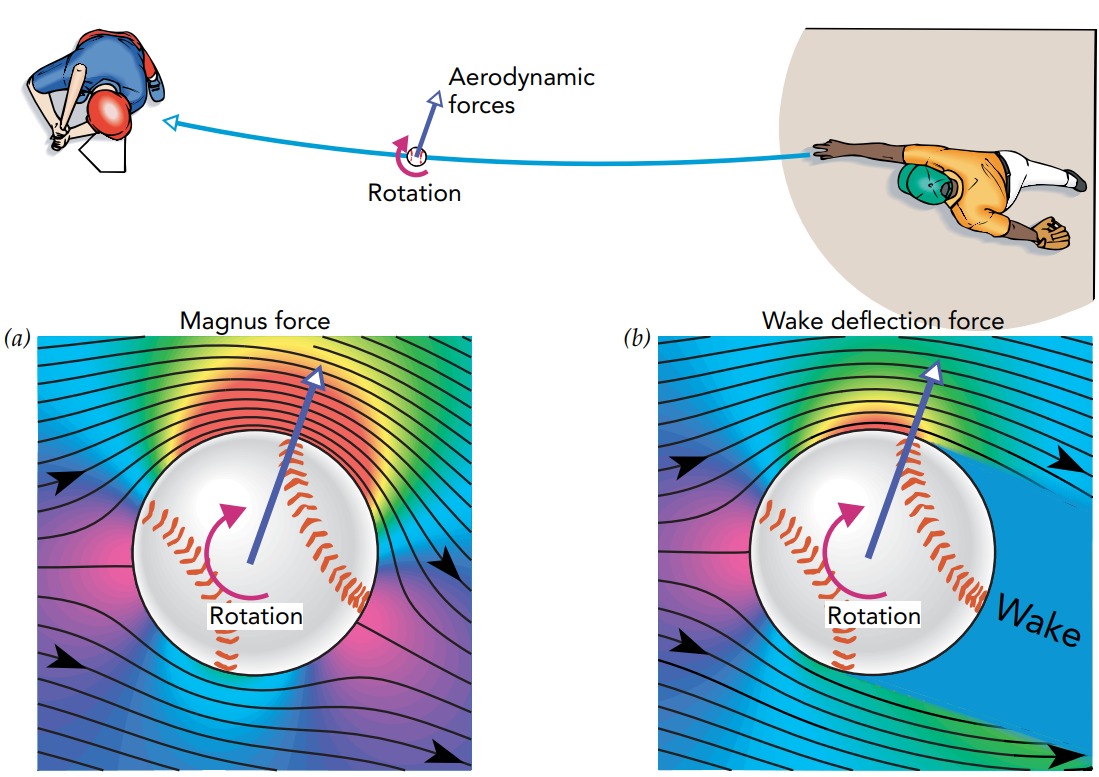
A curveball is thrown by making the ball spin rapidly about an axis perpendicular to its direction of motion. The choice of this axis determines which way the ball curves. In Fig., the ball is spinning clockwise, as viewed from above. With this choice of rotation axis, the ball curves to the pitcher’s right because the ball experiences two lift forces to the right. One is the Magnus force, named after the German physicist H. G. Magnus (1802–1870) who discovered it. The other is a force we will call the wake deflection force.
The Magnus force occurs because the spinning ball carries some of the viscous air around with it (Fig.). The steady-state flow pattern that forms around this ball is asymmetric: the airstream that moves with the turning surface is much longer than the airstream that moves opposite that surface. Since the longer airstream bends mostly toward the baseball, the average pressure on that side of the ball must be below atmospheric. The shorter airstream bends mostly away from the ball, so the average pressure on that side of the ball must be above atmos pheric. Because the pressure forces on the ball’s sides don’t balance one another, the ball experiences the Magnus force toward the low-pressure side—the side turning toward the pitcher—and deflects in that direction. The airflow deflects in the opposite direction.
In laminar flow, the Magnus force is the only lift force acting on a spinning object. However, a pitched baseball has a turbulent wake behind it and is also acted on by the wake deflection force. This force appears when the ball’s rapid rotation deforms the wake that develops behind it at high Reynolds numbers. When the ball isn’t spinning, the freely flowing airstream separates from the ball approximately at its side and that separation is symmetrical all the way around the ball’s middle (Fig.). However, when the ball is spinning (Fig.), the moving surface pushes on the airstream with viscous forces. As a result, airstream separation is delayed on one side of the ball and hastened on the other. The overall wake of air behind the ball is thus deflected to one side, and the ball experiences the wake deflection force toward the opposite side—the side turning toward the pitcher. The wake deflection force and the Magnus force both push the ball in the same direction.
A rapidly rotating baseball experiences two lift forces that cause it to curve in flight.
- (a) The Magnus force occurs because air flowing around the ball in the direction of its rotation bends mostly toward it, while air flowing opposite its rotation bends mostly away from it.
- (b) The wake deflection force occurs because air flowing around the ball in the direction of its rotation remains attached to the ball longer and the ball’s wake is deflected.
Of these two forces, the wake deflection force is probably the more important for a curveball, although the Magnus force is usually given all the credit. A skillful pitcher can make a ball curve about 0.3 m (12 in) during its flight from the mound to home plate—the more spin, the more curve. The pitcher counts on this change in direction to confuse the batter. The pitcher can also choose the direction of the curve by selecting the axis of the ball’s rotation. The ball will always curve toward the side of the ball that is turning toward the pitcher. When thrown by a right-handed pitcher, a proper curveball curves down and to the left, a slider curves horizontally to the left, and a screwball curves down and to the right.
When the pitcher throws a ball with backspin, so that the top of the ball turns toward the pitcher, the ball experiences an upward lift force. In baseball this force isn’t strong enough to overcome gravity, but it does make the pitch hang in the air for an unusually long time and appear to “hop.” Not surprisingly, a fastball thrown with strong backspin is called a hanging fastball. A fastball thrown with relatively little spin falls naturally and is called a sinking fastball. In golf, where the club can give the ball enormous backspin, the ball really does lift itself upward so that it flies down the fairway like a glider.
There are, however, some interesting cases when a ball’s behavior stems from its lack of spin. In baseball, for example, a knuckleball is thrown by giving the ball almost no rotation. The ball’s seams are then very important. As air passes over a seam, the flow is disturbed so that the ball experiences a sideways aerodynamic force, a lift force. The ball flutters about in a remarkably erratic manner. Releasing the ball without making it spin is difficult and requires great skill. Pitchers who are unable to throw a knuckleball legally sometimes resort to lubricating their fingers so that the ball slips out of their hands without spinning. Like its legal relative, this so-called spitball dithers about and is hard to hit. The same is true for a scuffed ball.