Flashlights
A flashlight is an electrical device. It contains an electric circuit, and most of its components are involved in the flow of electricity. To understand how a flashlight works, we need to understand how an electric circuit works and how electricity carries power from batteries to a lightbulb or LED.
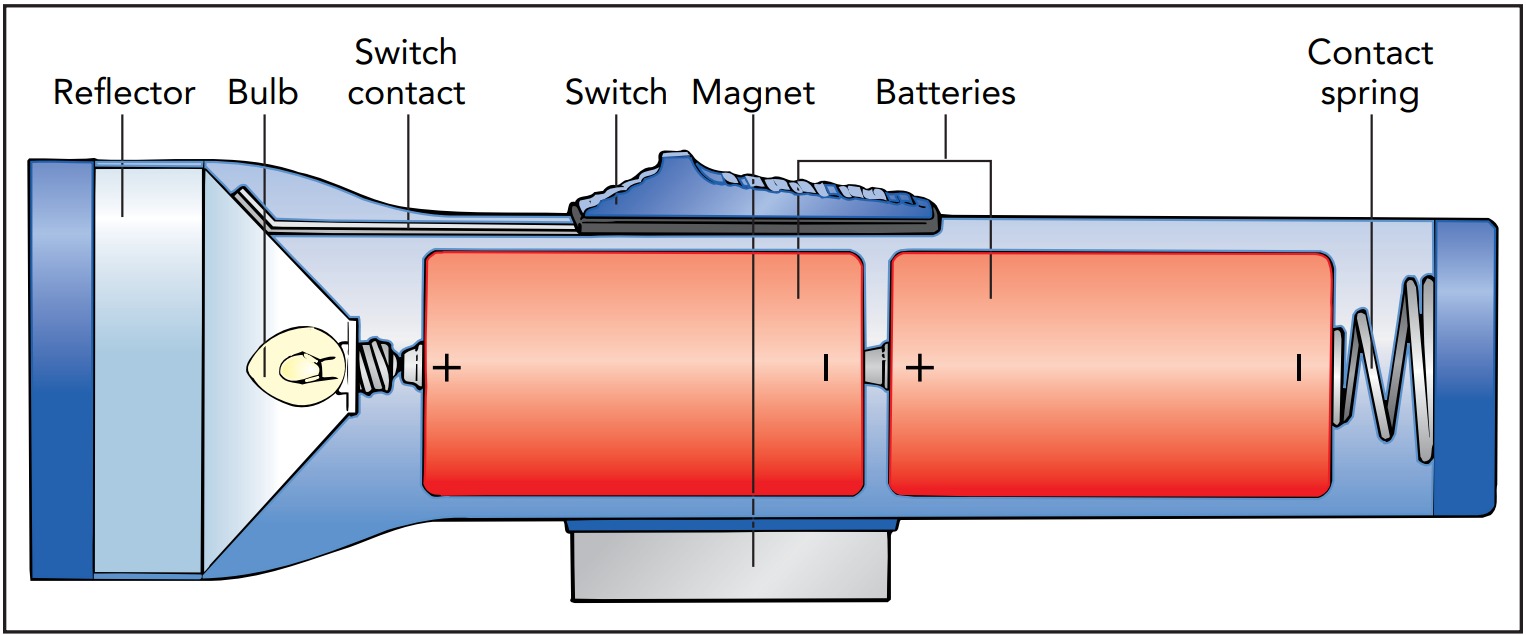
Electricity and the Flashlight's Electric Circuit
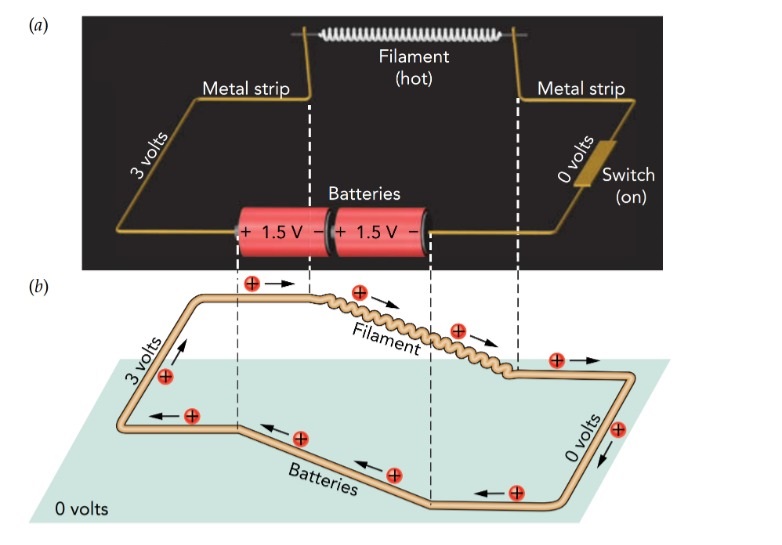
A basic, old-fashioned flashlight has just three components—a battery, a lightbulb, and a switch—connected together by metal strips. When the switch is on, the strips transfer energy from the batteries to the bulb. When you turn on a flashlight, electricity conveys energy from the batteries to the bulb. An electric current, a current of electric charges, flows through these components, carrying the energy with it. It can be visualized as a steady stream of tiny positive charges following a circular route that takes them through the batteries, through the bulb, and then back to the batteries for another trip. As long as the flashlight is on, charges flow around this loop, receiving energy from the batteries and delivering it to the bulb, over and over again. On route, the charges carry this energy mostly as electrostatic potential energy. The looping path taken by charges in a flashlight is called an electric circuit. Because a circuit has no beginning or end, charges can't accumulate in one place, where their mutual repulsion would eventually stop them from flowing.
Circuits are present in virtually all electric devices, and they explain the need for at least two wires in the power cord of any home appliance: one wire carries charges to the appliance to deliver energy, and the other wire carries those charges back to the power company to receive some more. As part of one conducting path between the batteries and bulb, the switch can make or break the flashlight's circuit. When the flashlight is on, the switch completes the loop so that charges can flow continuously around the closed circuit. However, when you turn off the flashlight, the switch breaks the loop to form an open circuit. Although one conducting path still connects the batteries and bulb, the loop now has a gap in it and can no longer carry a continuous current. Instead, charges accumulate at the gap, and current stops flowing through the flashlight. Since energy can no longer reach the bulb, it goes dark.

A short circuit forms when the two separate paths connecting the batteries to the bulb accidentally touch one another. This unintended contact creates a new, shorter loop around which the charges can flow. Because the bulb is expected to extract energy from the charges, it's designed to impede their flow and to convert their electrostatic potential energy into thermal energy and light. This opposition to the flow of electricity is called electrical resistance. Since the shortened loop offers little resistance, most of the charges flow through it, bypassing the bulb. The bulb dims or goes out altogether.
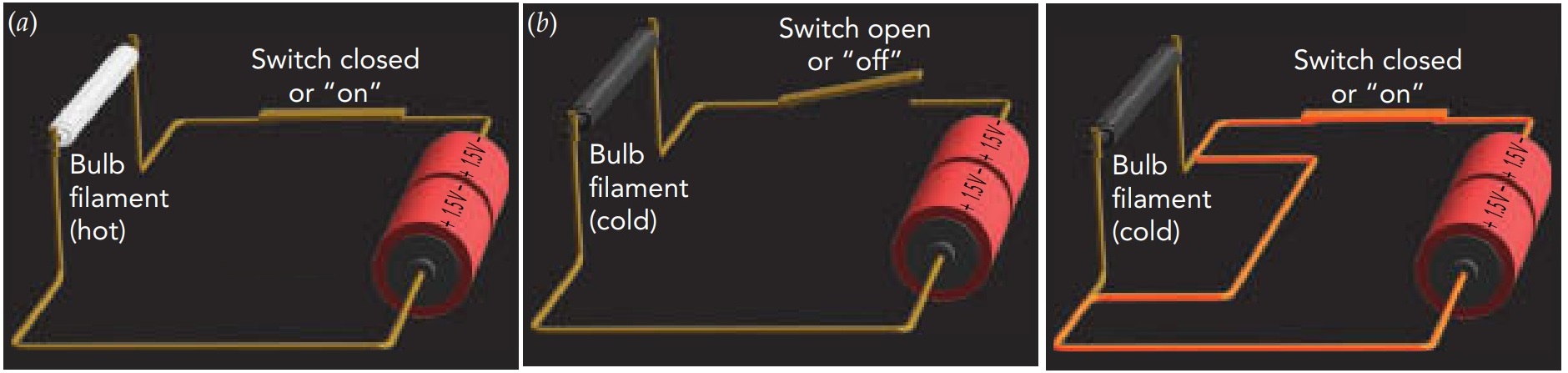
Since the bulb is the only part of the flashlight that's designed to consume electric energy, a short circuit leaves the charges without a safe place to get rid of their electrostatic potential energy. They deposit it dangerously in the batteries and the metal paths, making them hot. Since short circuits can start fires, flashlights and other electric equipment are designed to avoid them. Many modern flashlights use one or more light-emitting diodes (LEDs) in place of the old-fashioned bulb.
The Electric Current in the Flashlight
Each of the tiny charged particles flowing through the flashlight's circuit carries with it just a single elementary unit of electric charge and a miniscule amount of electrostatic potential energy. However, because those charges flow in astonishing numbers, they convey a considerable amount of energy per second—the quantity is power and measured in watts (abbreviated W). The bulb needs a certain amount of power to keep its filament glowing brightly, and you can determine how much power is reaching the bulb by multiplying the number of elementary charges passing through the bulb each second by the amount of energy each one delivers. The amount of charge passing a particular point in the circuit per unit of time is termed as the circuit's current. The SI unit of current is the coulomb per second, more commonly called the ampere (abbreviated A). One ampere corresponds to 1 C of charge passing by the designated point each second. One coulomb is roughly 6.25 × 1018, or 6,250,000,000,000,000,000, elementary charges, so even a 1-A current involves a tremendous flow of elementary charges.
Current has a direction, pointing along the route of positive charge flow. When you turn on the flashlight, charge flows around from the battery chain's positive terminal, through the bulb's filament, through the switch, and into the battery chain's negative terminal. The electric current is carried by negatively charged electrons heading in the opposite direction**. The positive charges that flow clockwise around the circuit are fictitious.
Batteries
A battery is basically a portable source of electric power. Batteries can be reassembled as a water pump. It "pumps" charge from low voltage to high voltage, much as a water pump pumps water from a low altitude to a high altitude or as a second water pump pumps water from low pressure to high pressure. Once again, our voltage ↔ altitude and voltage ↔ pressure analogies are helpful. Each pump moves something against its natural direction of flow, pushing it forward and doing work on it in the process. The battery increases a charge's electrostatic potential energy by pushing it up a voltage gradient.
The second perspective on batteries is more mechanical: a battery is a chemically powered machine. It uses chemical forces to transfer charges from its negative terminal to its positive terminal. As positive charges accumulate on the battery's positive terminal, the voltage rises there, and as negative charges accumulate on the battery's negative terminal, the voltage drops there. Since the battery does work transferring charges from low voltage to high voltage, it is converting its chemical potential energy into electrostatic potential energy in these separated charges.
A battery's rated voltage reflects its chemistry, specifically the amount of chemical potential energy it has available for each charge transfer. As the voltage difference between its terminals increases, so does the energy required for each charge transfer. Eventually, the chemicals can't do enough work on a charge to pull it away from the negative terminal and push it onto the positive terminal, so the transfers stop. The battery is then in equilibrium— the electrostatic forces opposing the next charge transfer exactly balance the chemical forces promoting it. A typical alkaline battery reaches this equilibrium when the voltage of its positive terminal is 1.5 V above the voltage of its negative terminal. Lithium batteries, with their more energetic chemistries, can achieve voltage differences of 3 V or more.
When you turn on the flashlight, you upset its equilibrium by allowing charges to leave the battery's negative terminal for its positive terminal. With fewer separated charges now. on its terminals, the battery's voltage difference decreases slightly and it begins pumping charges again. That renewed charge transport replenishes the terminals' separated charges and opposes any further decrease in the battery's voltage. In this manner, a 1.5-V alkaline battery maintains a nearly steady voltage difference of 1.5 V between its terminals, whether its flashlight is on or off.
That alkaline battery is powered by an electrochemical reaction in which powdered zinc at its negative terminal reacts with manganese dioxide paste at its positive terminal. This reaction resembles controlled combustion. In effect, the battery "burns" zinc to obtain the energy it needs to pump charges from its negative terminal to its positive terminal. However, as the battery consumes its chemical potential energy, its ability to pump charges diminishes. When its chemicals are nearly exhausted, the battery's increasing disorder reduces its voltage. An aging battery can pump less current than a fresh one, and it provides that current with less voltage. Ultimately, less power reaches the flashlight's bulb and it goes dim.
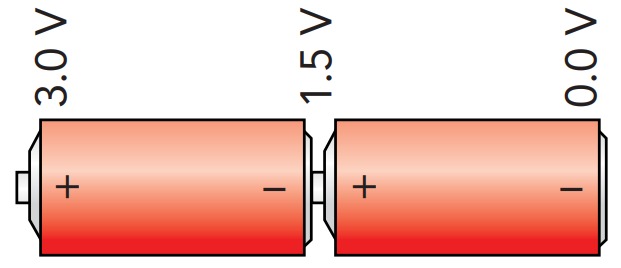
Most flashlights use more than one battery. When two alkaline batteries are connected together in a chain, so that the positive terminal of one battery touches the negative terminal of the other, the two batteries work together to pump charges from the chain's negative terminal to its positive terminal. Each battery pump charges until its positive terminal is 1.5 V above its negative terminal, so the chain's positive terminal is 3.0 V above its negative terminal. Because charges never leave the flashlight's circuit, only relative voltages matter in that circuit. The more batteries in the flashlight's chain, the more energy a charge receives overall and the more the voltage will increase from the chain's negative terminal to its positive terminal. A flashlight that uses six alkaline batteries in its chain has a positive terminal that is 9 V above its negative terminal.
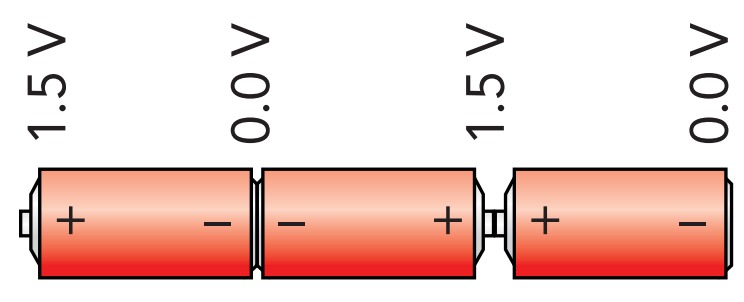
If you reverse one of the batteries in a chain, the reversed battery will extract energy from any charge passing through it (Fig. 10.3.8). While the chain may still pump charge from its negative terminal to its positive terminal, its overall voltage will be reduced because, instead of adding 1.5 V to the chain's overall voltage, the reversed battery will subtract that amount. If the chain has three batteries, two will add energy to the charge while the third will subtract it, and the chain's overall voltage will be only 1.5 V.
As the reversed battery extracts energy from the charges passing through it, at least some of that extracted energy is converted into chemical potential energy. The reversed battery is recharging! Battery chargers follow that concept, pushing current backward through a battery—from its positive terminal to its negative terminal—to restore the chemical potential energy in a rechargeable battery. However, normal alkaline batteries are "*** non-rechargeable ***," meaning that they turn most of the recharging current's energy into thermal energy instead of chemical potential energy. Non-rechargeable batteries may overheat and explode during recharging.
Bulbs and Metal Strips
Whereas a battery gives charges electrostatic potential energy by pushing them up a voltage gradient, a bulb releases that electrostatic potential energy by letting charges slide down another voltage gradient. Those two devices make a perfect pair: the battery provides electric power, and the bulb consumes it. The bulb uses this power to heat its tungsten filament so hot that it glows yellow-white.
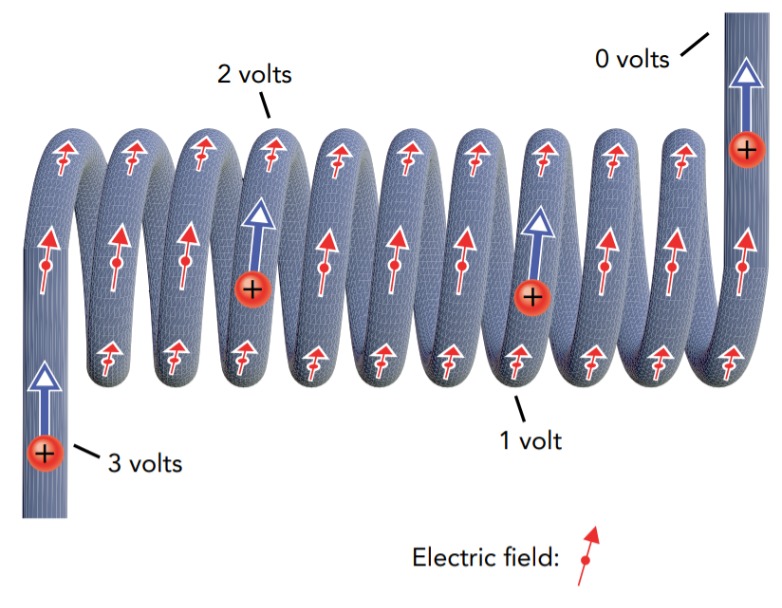
Consider a flashlight with two alkaline batteries. The bulb's filament is a fine wire, and its two ends are electrically connected to the battery chain's terminals. With one end at 3.0 V and the other at 0.0 V, the filament has a voltage gradient across it and therefore an electric field. While a conductor has a uniform voltage when its charges are in equilibrium, the charges in the bulb are in equilibrium only when the flashlight is off. When you switch the flashlight on, you impose a 3.0-V difference between the two ends of the filament and the filament's charges immediately begin accelerating down the voltage gradient toward the 0.0-V end.
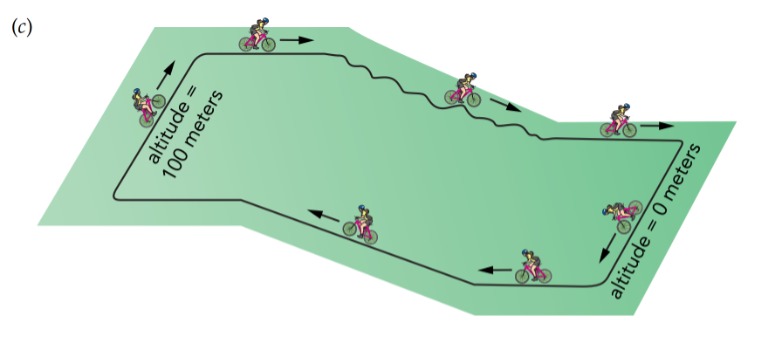
In our voltage-altitude analogy, it's as though you suddenly tilted a level field to create a hill, and water that had been lying motionless on that field now accelerated downhill. However, a better analog to the individual charges that we're considering at the moment would be bicyclists. Picture hundreds of bicyclists on a level field that suddenly tilts to form a hill. All the bicyclists that were at equilibrium on the level field now accelerate downhill. If the filament were a perfect conductor of electricity, each charge would accelerate steadily down the voltage gradient and convert its electrostatic potential energy into kinetic energy. However, the filament has a large electrical resistance—it significantly impedes the flow of electric current. Instead of accelerating smoothly from one end of the filament to the other, each charge bounces its way down the voltage gradient, colliding frequently with the filament's tungsten atoms and giving up kinetic energy with each collision. What began as ordered electrostatic potential energy in the charges becomes thermal energy in the tungsten atoms, and the filament glows brightly. Referring again to our voltage ↔ altitude analogy, picture the bicyclists riding down a rough hill strewn with rocks and trees. They pick up bruises instead of speed.
The metal strips are excellent conductors, but like all ordinary electrical wires, they're not quite perfect. Each strip has a small electrical resistance, so charges can't coast through it because of inertia alone. Instead, the charges need a small voltage gradient to keep them moving forward, and they emerge from the strip at a slightly lower voltage than where they entered. The missing energy has become thermal energy, slightly heating the metal strip. In general, the less electrical resistance in the strips carrying current to and from the bulb, the less power is wasted on the route and the more power reaches the bulb. That's why it's so important to use thick metal strips or even the flashlight's metal case in the connections. A poor connection anywhere in the circuit can spoil this efficient transfer of power. If there is dirt or grease on a battery terminal or worn materials in the switch, the current will have to pass through a large electrical resistance and waste power. Improving that connection, either by shaking the flashlight or by cleaning the metal surfaces, will increase the current flow through the circuit, reduce the wasted power, and brighten the flashlight.
Voltage, Current, and Power in Flashlights
When you turn on the flashlight, an electric current carries power from its two alkaline batteries to its bulb. A bulb consumes electric power because the current passing through it slides down the voltage gradient and there is a drop in voltage between where the current arrives at the filament and where it leaves the filament. This voltage drop measures the electrostatic potential energy each unit of charge loses while struggling through the filament. Multiplying the voltage drop by the current passing through the bulb gives you the power consumed by the bulb.
[ P = VI]
Similarly, A battery chain produces electric power because the current passing through it is pushed up a voltage gradient and there is a rise in voltage between where the current arrives at the battery chain and where it leaves the battery chain. This voltage rise measures the electrostatic potential energy each unit of charge gains while being pumped through the batteries. Multiplying the voltage gain by the current passing through the batteries gives you the power provided by the batteries.
Choosing the Bulb: Ohm's Law
The bulb's filament must clearly match the flashlight, particularly the voltage of the flashlight's battery chain. If you were to use the wrong bulb in this flashlight, one designed for a different voltage drop, its filament would carry the wrong amount of current and receive the wrong amount of power. Too much power would quickly burn out its filament, while too little power would make the filament glow dimly. The relationship between current and voltage drop is the result of collisions. Charges effectively stop each time they crash into metal atoms, so they need the push of an electric field to keep them moving forward. Doubling that electric field doubles each charge's average speed and, because the number of mobile charges in the filament is fixed, also doubles the overall current flowing through the filament. Since the electric field that propels this current is the filament's voltage gradient, doubling the voltage drop through the filament doubles the current as well.
The influence of filament choice on current flow reflects the different electrical resistances of those filaments. Anything that increases the number of mobile electric charges across the filament's width or allows those charges to maintain a higher average speed for a given voltage drop will decrease the filament's electrical resistance and increase the current flowing through it. Electrical resistance is defined as the voltage drop through the filament divided by the current that arises as a result. Making the filament thicker or shorter will lower its resistance, as will changing its composition to make collisions less frequent.
the current flowing through the filament is proportional to the voltage drop through it and inversely proportional to the filament's electrical resistance, which can be written as:
\[current = \frac{voltage~ drop}{electrical~ resistance}\]
This relationship is called Ohm's law, after its discoverer Georg Simon Ohm. Structuring the relationship this way separates the causes (voltage drop and electrical resistance) from their effect (current flow). However, this equation is often rearranged to eliminate the division. The relationship then takes its customary form, which can be written as a word equation:
\[ voltage~ drop = current \times electrical~ resistance\]
in symbols:
\[V = I · R\]
and in everyday language:
Long, skinny jumper cables have large resistances. When you connect them to a battery to jumpstart your car, they'll carry a relatively small current and your car probably won't start.
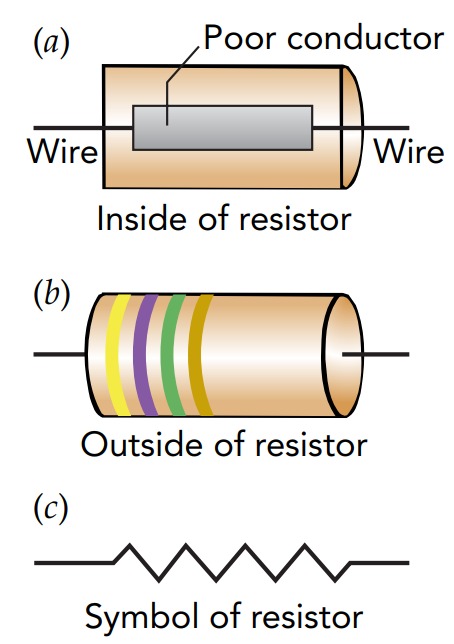
The SI unit of electrical resistance, the volt per ampere, is called the ohm (abbreviated \(\Omega\), the Greek letter Omega). Despite its simplicity, Ohm's law is extremely useful in physics and electrical engineering. It applies to so many systems that nearly everything is ohmic, that is, can be characterized by an electrical resistance. Devices that obey Ohm's law are common in modern technology, often as simple electronic components known as resistors. A resistor carries a current equal to its voltage drop divided by its resistance, and it experiences a voltage drop equal to the current it carries times its resistance.
Finally, an object's electrical resistance is typically temperature-dependent. Rising temperature increases the number of mobile charges in an object but also makes them collide more frequently with the jiggling atoms. If the increasing collision frequency dominates, as it does in metals, an object's resistance increases with temperature. For example, a filament carries less and less current as it approaches operating temperature, a behavior that helps it avoid overheating. However, if the increase in mobile charges dominates, as it does in semiconductors, an object's resistance decreases with temperature. This explains why semiconductor-based computer chips carry more and more current as they get hotter and will self-destruct at excessive temperatures.
LED Flashlights: Series and Parallel Circuits
Unfortunately, lightbulbs drain flashlight batteries quickly and burn out at inconvenient times. Since LEDs are much more energy efficient than bulbs and last almost forever, it's no surprise that LED flashlights are rapidly replacing bulb flashlights.
LEDs are sophisticated semiconductor devices that conduct zero current when the voltage drop across it is less than a threshold voltage of about 2–4 V, depending on color, and it conducts a large, potentially damaging current when the voltage drop is significantly more than that threshold. Because small changes in voltage drop across the LED dramatically change the current passing through it, the LED is difficult to control on its own. That's why an LED is often paired with a resistor.
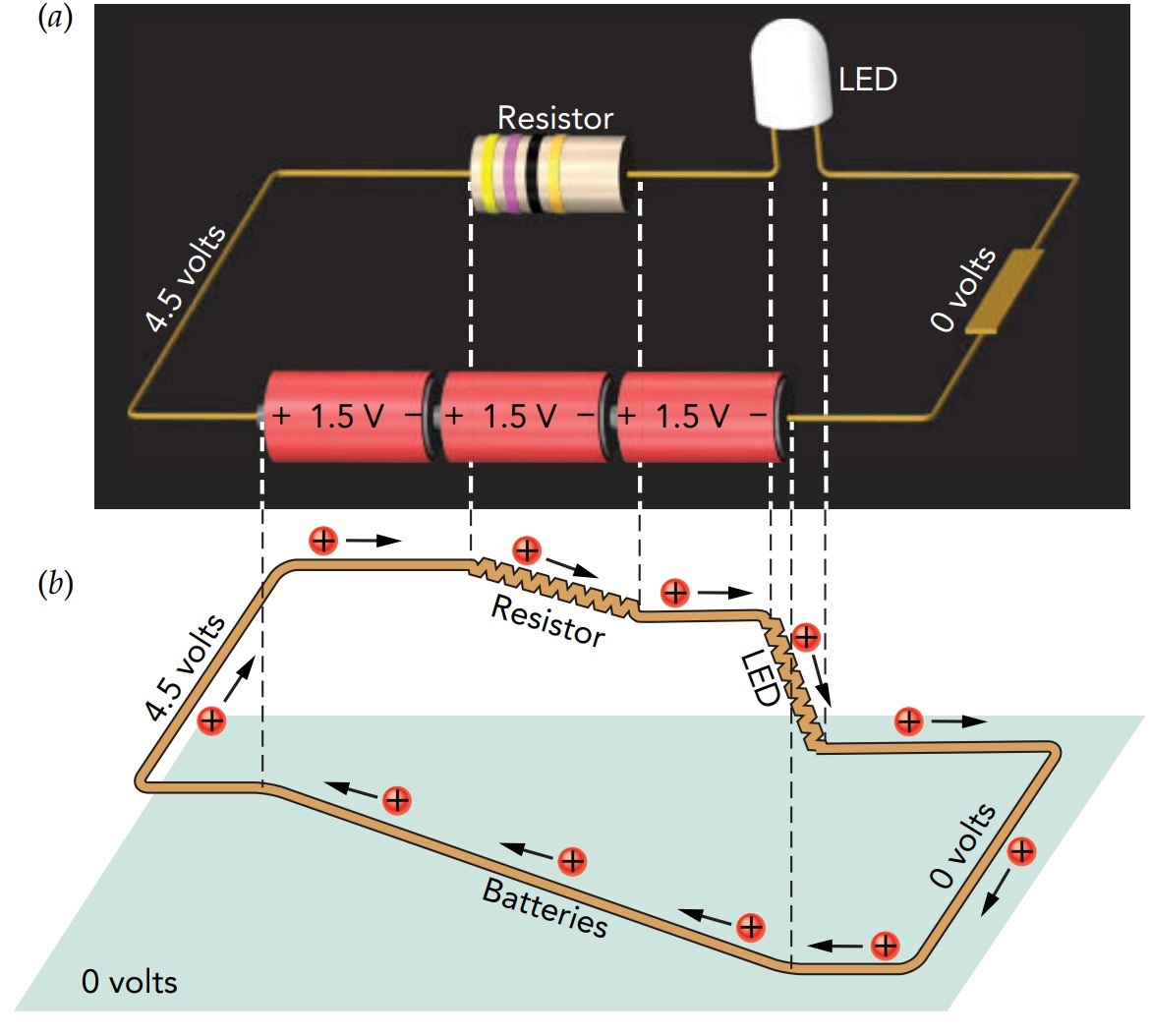
In a simple LED flashlight, the current leaving the positive terminal of the batteries flows sequentially through a resistor and an LED before returning to the negative terminal of the batteries. That arrangement, in which the same current flows sequentially through each component, is known as a series circuit. Although all the components in a series circuit carry the same current, they share the circuit's overall voltage drop.
The overall voltage drop available to the LED flashlight's power-consuming components is equal to the voltage rise provided by its batteries. Because they are in series, the resistor and the LED must share that overall voltage drop (neglecting the small voltage drops in the metal strips and switch). Since they also carry the same current, the resistor's ohmic behavior limits the current passing through the entire circuit, including the LED. In effect, the resistor and LED negotiate—each component takes enough of the overall voltage drop to allow it to conduct the same current as the other component. Following the negotiation, the voltage drop across the LED is slightly more than its threshold voltage and the rest of the overall voltage drop is taken by the resistor. The resistor is chosen so that, when subject to that voltage drop, it conducts the right amount of current to power the LED properly.


When an LED flashlight has more than one LED, the flashlight must supply each with current. This is usually done by dividing the current from the batteries into parts and sending one part through each of the LEDs. That arrangement, in which the current is divided into parts that flow simultaneously through each component, is known as a parallel circuit. Although each component in a parallel circuit carries its own fraction of the overall current, all the components experience the same voltage drop.
In a typical multiple-LED flashlight, each LED is actually paired with a resistor to regulate its current. The flashlight thus combines parallel and series circuits. Each LED and its resistor are connected in series, so they carry the same current but share the overall voltage drop. The multiple LED-resistor pairs are connected in parallel, so they carry separate portions of the circuit's overall current but experience the same voltage drop