Superconductivity
The phenomenon of superconductivity, in which the electrical resistance of certain materials completely vanishes at low temperatures, is one of the most interesting and sophisticated in condensed matter physics. It was first discovered by the Dutch physicist Heike Kamerlingh Onnes, who was the first to liquefy helium (which boils at 4.2 Kelvin at standard pressure). In 1911 Kamerlingh Onnes and one of his assistants discovered the phenomenon of superconductivity while studying the resistance of metals at low temperatures. They studied mercury because very pure samples could easily be prepared by distillation.
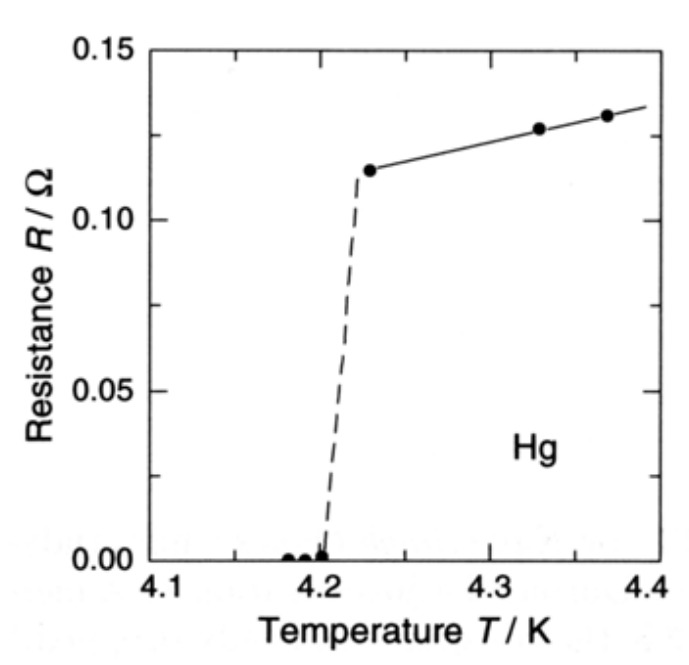
As in many other metals, the electrical resistance of mercury decreased steadily upon cooling, but dropped suddenly at 4.2 K, and became undetectably small. Soon after this discovery, many other elemental metals were found to exhibit zero resistance when their temperatures were lowered below a certain characteristic temperature of the material, called the critical temperature, Tc.
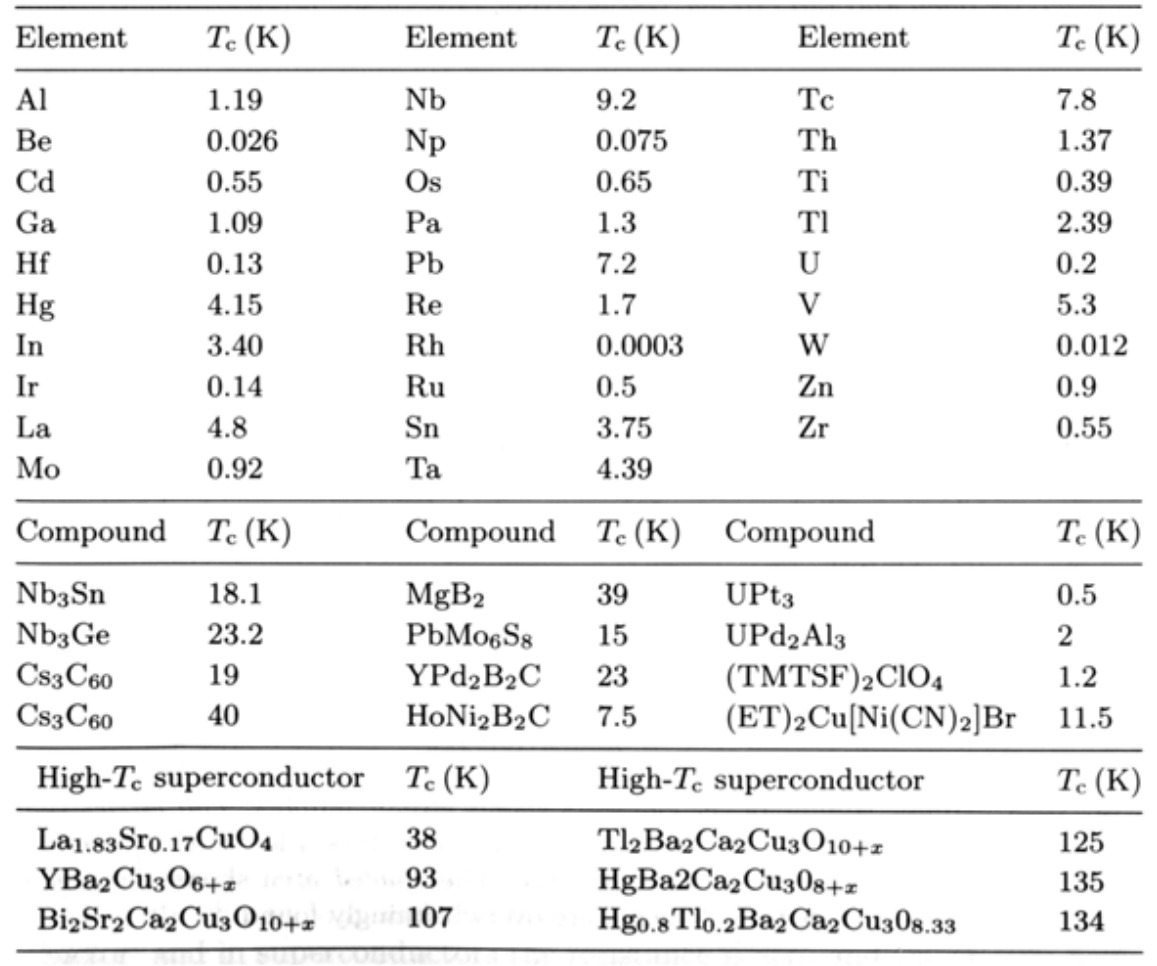
The Meissner effect
In 1933, Walter Meissner and Robert Ochsenfeld discovered a magnetic phenomenon that showed that superconductors are not just perfect conductors. Imagine that both the ideal conductor and superconductor are above their critical temperature, Tc. That is, they both are in a normal conducting state and have electrical resistance. A magnetic field, B a, is then applied. This results in the field penetrating both materials. Both samples are then cooled so that the ideal conductor now has zero resistance. It is found that the superconductor expels the magnetic field from inside it, while the ideal conductor maintains its interior field. Note that energy is needed by the superconductor to expel the magnetic field. This energy comes from the exothermic superconducting transition. Switching off the field induces currents in the ideal conductor that prevent changes in the magnetic field inside it – by Lenz’s law. However, the superconductor returns to its initial state, i.e. no magnetic field inside or outside it.
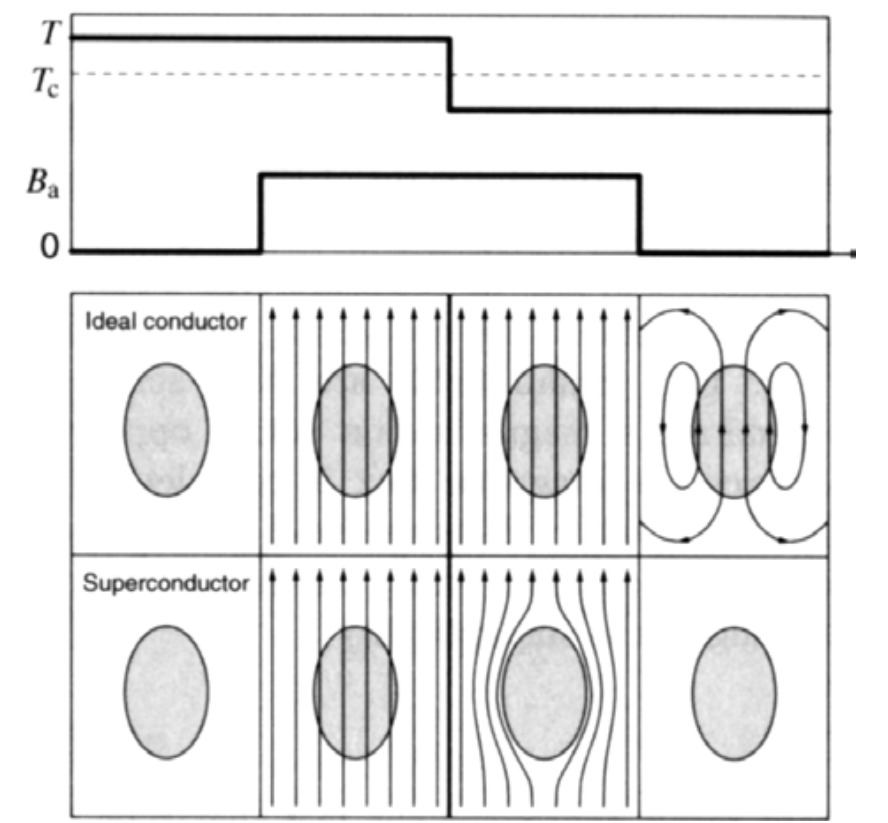
Type 1 and 2 superconductors
High magnetic fields destroy superconductivity and restore the normal conducting state. Depending on the character of this transition, we may distinguish between type 1 and 2 superconductors. It is found that the internal field is zero (as expected from the Meissner effect) until a critical magnetic field, Bc, is reached where a sudden transition to the normal state occurs. This results in the penetration of the applied field into the interior. Superconductors that undergo this abrupt transition to the normal state above a critical magnetic field are known as type 1 superconductors. Most of the pure elements tend to be type 1 superconductors. Type 2 superconductors, on the other hand, respond differently to an applied magnetic field. An increasing field from zero results in two critical fields, Bc1 and Bc2. At Bc1, the applied field begins to partially penetrate the interior of the superconductor. However, the superconductivity is maintained at this point. The superconductivity vanishes above the second, much higher, critical field, Bc2. For applied fields between Bc1 and Bc2, the applied field is able to partially penetrate the superconductor, so the Meissner effect is incomplete, allowing the superconductor to tolerate very high magnetic fields.
Type 2 superconductors are the most technologically useful because the second critical field can be quite high, enabling high field electromagnets to be made out of superconducting wire. Wires made from say niobium-tin (Nb3Sn) have a Bc2 as high as 24.5 Tesla – in practice it is lower. This makes them useful for applications requiring high magnetic fields, such as Magnetic Resonance Imaging (MRI) machines. The advantage of using superconducting electromagnets is that the current only has to be applied once to the wires, which are then formed into a closed loop and allow the current (and field) to persist indefinitely – as long as the superconductor stays below the critical temperature. That is, the external power supply can be switched off. As a comparison, the strongest permanent magnets today may be able to produce a field close to 1 Tesla. However, it is possible to obtain up to 24.5 Tesla from a niobium–tin superconductor. There is a misconception amongst some non-specialists that the term "Type 2" refers to the copper oxide based high temperature superconductors discovered in the late 1980s. While these are type 2 superconductors, so are many superconductors discovered before that time.
Why is a levitated magnet stable?
A common demonstration of the Meissner effect is to cool a high Tc superconductor (Y B a2Cu3O7), then place a small and strong permanent magnet on top of it to demonstrate the repulsion of the magnetic field by the superconductor. This repulsion results in the levitation of the magnet. An explanation for this levitation is that the magnet “sees” a mirror image of itself in the superconductor, which is like a magnet floating on top of another identical magnet. This would be true if the superconductor was much larger than the magnet. In practice the superconductor may be only slightly larger than the magnet. This will result in a distorted image of the magnet, especially near the edges of the superconductor. The situation then is similar to trying to balance two magnets on top of each other. If you have ever tried to balance one magnet on top of another, you would have quickly found that it is impossible to do without physically holding it there. Left alone, the magnet will always topple over and never stay levitated. This is a well known effect in physics, a consequence of Earnshaw’s theorem, which states that there can never be any stable configuration of magnetic fields that will trap another magnet.
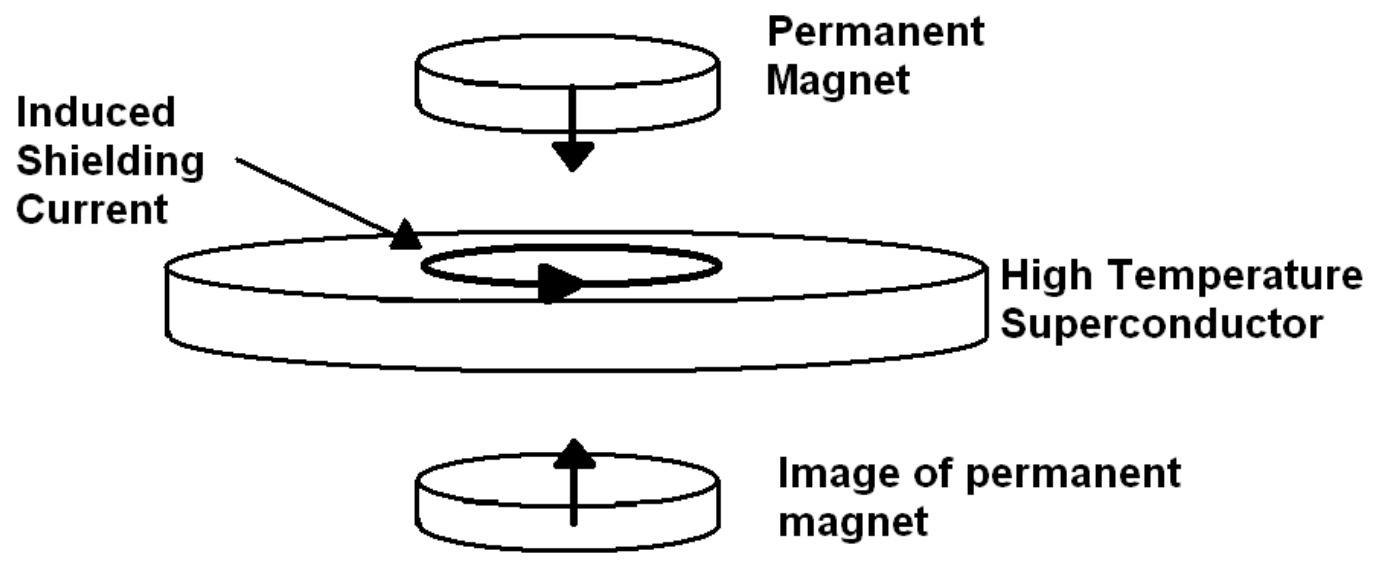
So why does a levitating permanent magnet remain stable on top of a small sized superconductor? Even a little nudge causes the magnet to spring back to its original position as if somehow tied by invisible springs to that point. To explain this, we need to expose everyone’s little secret when they demonstrate this levitation experiment. If the magnet is lightly placed over a newly cooled high temperature superconductor, you should find that the magnet does not stay levitated for long. It slips off very quickly as one would expect to happen if a magnet is placed on top of another magnet, or a distorted mirror image of itself in this case. Note what everyone does in order to get the magnet to levitate stably. They hold the magnet over the superconductor and rather than letting it go, they thrust it slightly towards the superconductor. Releasing the magnet at this point causes it to remain there stably. Incredibly, if the magnet is then removed then dropped back over the superconductor, it levitates stably without the need to thrust the magnet towards the superconductors. It is as if the superconductor has “remembered” that the magnet was there. Moving the magnet back and forth parallel to the surface of the superconductor or allowing the superconductor to warm up above Tc then cooling it down again will make the levitation of the magnet unstable once more. The magnet must again be thrust towards the superconductor to achieve stability. How can this behaviour be explained? It is because of the formation of vortex state and flux pinning phenomena exists in superconductors.
Vortex states and flux pinning
Stable levitation of a permanent magnet above a small and flat superconductor only occurs for type-2 superconductors. Certainly levitation occurs when using type-1 superconductors but in a type-2, the levitation is particular stable and robust. The answer lies in the properties of type-2 superconductors for an applied magnetic field between the two critical fields, Bc1 and Bc2. Earlier we said that for type-2, there is partial penetration of the magnetic field. This partial penetration is in the form of a regular array of normal conducting regions.
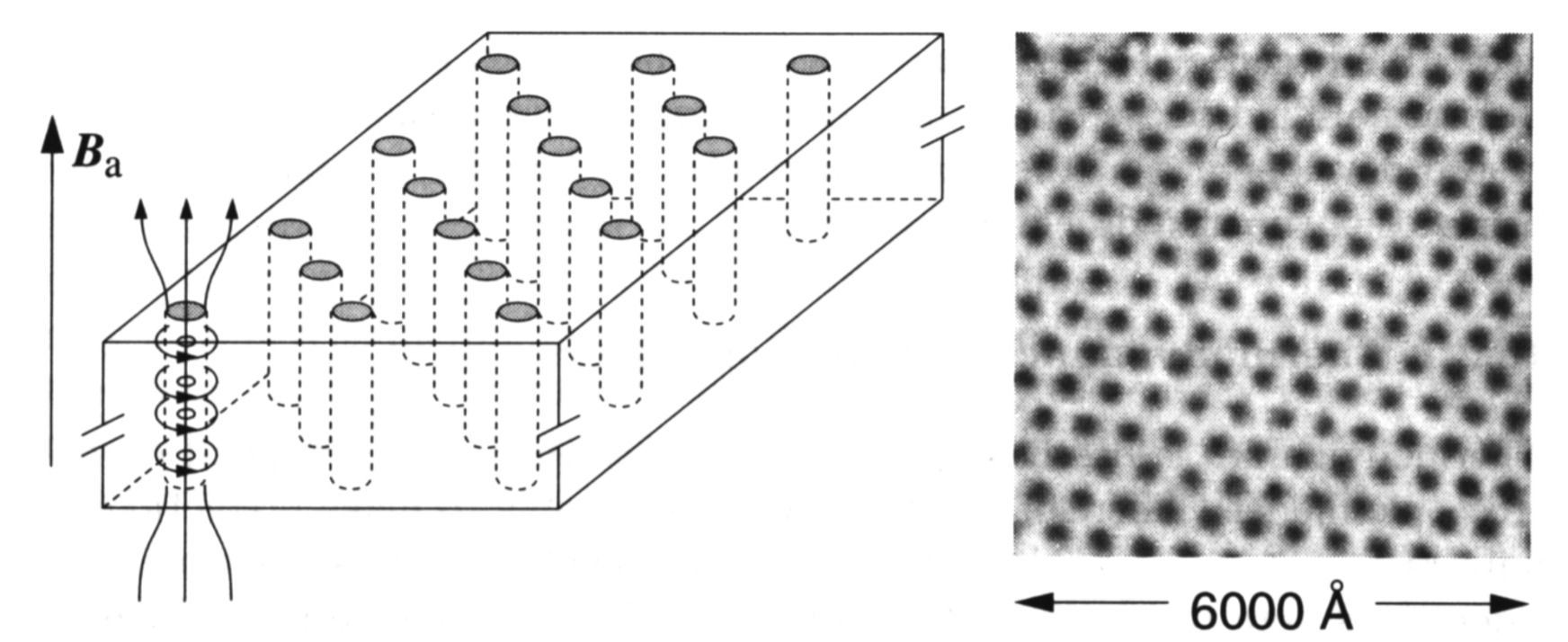
These normal regions allow the penetration of the magnetic field in the form of thin filaments, usually called flux lines, fluxons, fluxoids or vortices. The vortices are aptly named because each is a "vortex" or swirl of electrical current that are associated with this state. While in the vortex state, the material surrounding these normal can have zero resistance and has partial flux penetration. Vortex regions are essentially filaments of normal conductor (non-superconducting) that run through the sample when an external applied magnetic field exceeds the lower critical field, Bc1. As the strength of the external field increases, the number of filaments increases until the field reaches the upper critical value, Bc2, the filaments crowd together and join up so the entire sample becomes normal. One can view a vortex as a cylindrical swirl of current surrounding a cylindrical normal conducting core that allows some flux to penetrate the interior of type-2 superconductors. Thrusting a permanent magnet towards a type-2 superconductor will cause the applied magnetic field at the superconductor to be within the region of the two critical fields. This creates the vortex states. In principle, the motion of a levitating permanent magnet will cause these vortices to move. In practice, real materials (such as High Tc superconductors) have defects (missing or misplaced atoms, impurity atoms) in their crystal lattices. They are also composed of many crystals, all bound together, resulting in many crystal boundaries. The crystal defects and boundaries stop the motion of the vortices, which is known as flux pinning. This provides the stability of a levitating magnet. Pinning the motion of its magnetic field lines also means stopping the motion of the magnet. Note that flux pinning can only occur in type-2 superconductors. This demonstration with high temperature superconductors indicates that they are of type-2.
BCS theory and Cooper pairs
According to classical physics, part of the resistance of a metal is due to collisions between free electrons and the crystal lattice’s vibrations, known as phonons. In addition, part of the resistance is due to scattering of electrons from impurities or defects in the conductor. As a result, the question arose as to why this does not happen in superconductors?
A microscopic theory of superconductivity was developed in 1957 by John Bardeen, Leon Cooper and J Robert Schrieffer, which is known as the BCS theory. The central feature of the BCS theory is that two electrons in the superconductor are able to form a bound pair called a Cooper pair if they somehow experience an attractive interaction between them. This notion at first sight seems counterintuitive since electrons normally repel one another because of their like charges.
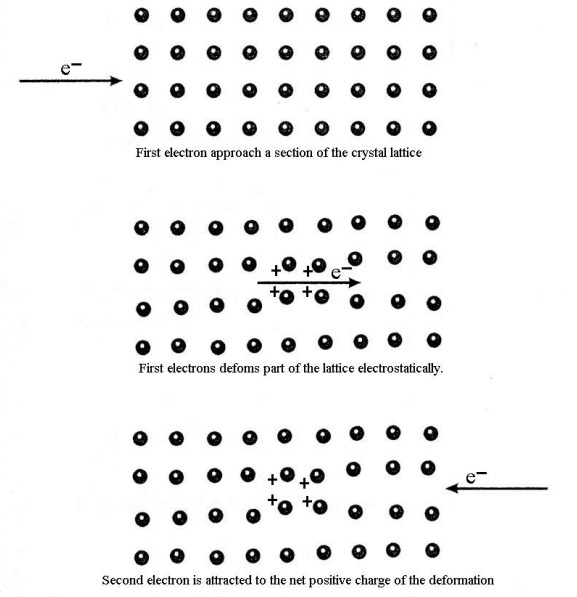
An electron passes through the lattice and the positive ions are attracted to it, causing a distortion in their nominal positions. The second electron (the Cooper pair partner) comes along and is attracted by the displaced ions. Note that this second electron can only be attracted to the lattice distortion if it comes close enough before the ions have had a chance to return to their equilibrium positions. The net effect is a weak delayed attractive force between the two electrons.
This short lived distortion of the lattice is sometimes called a virtual phonon because its lifetime is too short to propagate through the lattice like a wave as a normal phonon would. From the BCS theory, the total linear momentum of a Cooper pair must be zero. This means that they travel in opposite directions. In addition, the nominal separation between the Cooper pair (called the coherence length) ranges from hundreds to thousands of ions separating them! This is quite a large distance in atomic scale. If electrons in a Cooper pair were too close, such as a couple of atomic spacings apart; the electrostatic (coulomb) repulsion will be much larger than the attraction from the lattice deformation and so they will repel each other. Thus there will be no superconductivity. A current flowing in the superconductor just shifts the total moment slightly from zero so that, on average, one electron in a cooper pair has a slightly larger momentum magnitude that its pair. They do, however, still travel in opposite directions.
The interaction between a Cooper pair is transient. Each electron in the pair goes on to form a Cooper pair with other electrons, and this process continues with the newly formed Cooper pair so that each electron goes on to form a Cooper pair with other electrons. The end result is that each electron in the solid is attracted to every other electron forming a large network of interactions. Causing just one of these electrons to collide and scatter from atoms in the lattice means the whole network of electrons must be made to collide into the lattice, which is energetically too costly. The collective behaviour of all the electrons in the solid prevents any further collisions with the lattice. Nature prefers situations that spend a minimum of energy. In this case, the minimum energy situation is to have no collisions with the lattice. A small amount of energy is needed to destroy the superconducting state and make it normal. This energy is called the energy gap.
Although a classical description of Cooper pairs has been given here, the formal treatment from the BCS theory is quantum mechanical. The electrons have wave-like behaviour and are described by a wave function that extends throughout the solid and overlaps with other electron wave functions. As a result, the whole network of electrons behaves line one wave function so that their collective motion is coherent. In addition to having a linear momentum, each electron behaves as if it is spinning. This property, surprisingly, is called spin. This does not mean that the electron is actually spinning, but behaves as though it is spinning. The requirement from the BCS theory is that spins of a Cooper pair be in opposite directions.
High Tc superconductors
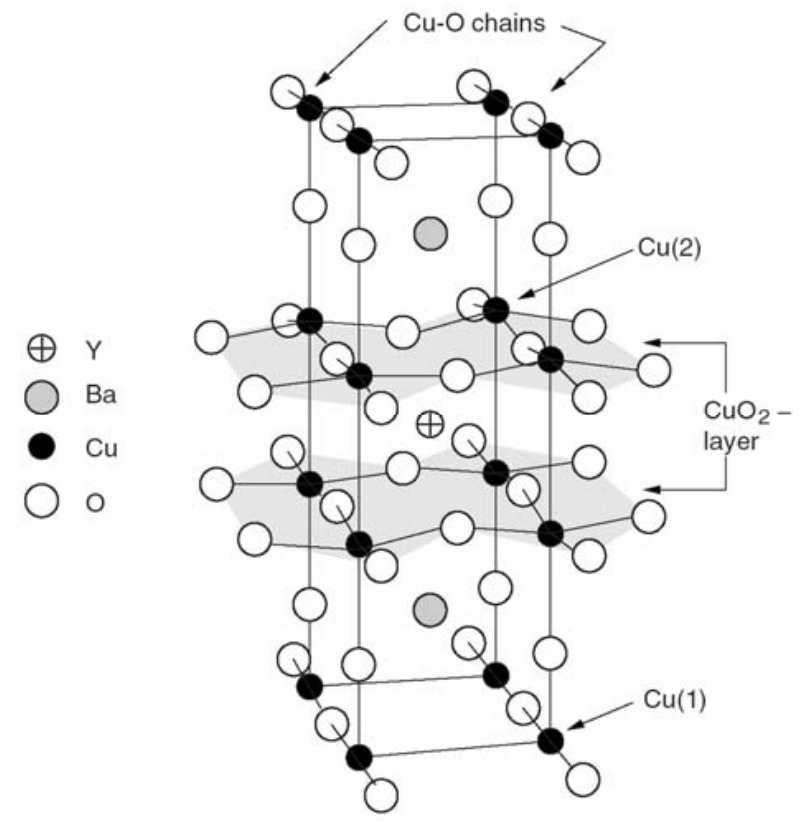
It has long been a dream of scientists working in the field of superconductivity to find a material that becomes a superconductor at room temperature. A discovery of this type will revolutionize every aspect of modern day technology such as power transmission and storage, communication, transport and even the type of computers we make. All of these advances will be faster, cheaper and more energy efficient. This has not been achieved to date. However, in 1986 a class of materials was discovered by Bednorz and Müller that led to superconductors that we use today on a bench-top with liquid nitrogen to cool them. Not surprisingly, Bednorz and Müller received the Nobel Prize in 1987 (the fastest-ever recognition by the Nobel committee). The material we mostly use on bench-tops is Yttrium Barium Copper Oxide, or Y B a2Cu3O7, otherwise known as the 1-2-3 superconductor, and are classified as high temperature (Tc) superconductors.
Critical temperatures as high as 135 K have been achieved. Whilst this is not room temperature, it has made experiments on superconductivity accessible to more people since these need only be cooled by liquid nitrogen (with a boiling point of liquid nitrogen is 77 K), which is cheap and readily available. This is in contrast to the expensive and bulky equipment that used liquid helium for cooling the traditional types of superconductors. Moreover, the superconductors are calculated to have an upper critical magnetic field, Bc2, of about 200 Tesla, its huge!
Unlike traditional superconductors, conduction mostly occurs in the planes containing the copper oxide. It has been found that the critical temperature is very sensitive to the average number of oxygen atoms present, which can vary. For this reason the formula for 1-2-3 superconductor is sometimes given as Y B a2Cu3O7 minus δ, where δ is a number between 0 and 1.
The nominal distance between cooper pairs (coherence length) in these superconductors can be as short as one or two atomic spacings. As a result, the coulomb repulsion force will generally dominate at these distances causing electrons to be repelled rather than coupled. For this reason, it is widely accepted that Cooper pairs, in these materials, are not caused by a lattice deformation, but may be associated with the type of magnetism present (known as antiferromagnetism) in the copper oxide layers. So high Tc superconductors cannot be explained by the BCS theory since that mainly deals with a lattice deformation mediating the coupling of electron pairs. The research continues into the actual mechanism responsible for superconductivity in these materials.
Applications of superconductors
The first large scale commercial application of superconductivity was in magnetic resonance imaging (MRI). This is a non-intrusive medical imaging technique that creates a two-dimensional picture of say tumors and other abnormalities within the body or brain. This requires a person to be placed inside a large and uniform electromagnet with a high magnetic field. Although normal electromagnets can be used for this purpose, because of resistance they would dissipate a great deal of heat and have large power requirements. Superconducting magnets on the other hand have almost no power requirements apart from operating the cooling. Once electrical current flows in the superconducting wire, the power supply can be switched off because the wires can be formed into a loop and the current will persist indefinitely as long as the temperature is kept below the transition temperature of the superconductor.
Superconductors can also be used to make a device known as a superconducting quantum interference device (SQUID). This is incredibly sensitive to small magnetic fields so that it can detect the magnetic fields from the heart, that is, 10to the power of minus 10 Tesla and even the brain, that is, 10to the power of minus 13 Tesla. For comparison, the Earth’s magnetic field is about 10to the power of minus 4 Tesla. As a result, SQUIDs are used in non-intrusive medical diagnostics on the brain. The traditional use of superconductors has been in scientific research where high magnetic field electromagnets are required. The cost of keeping the superconductor cool are much smaller than the cost of operating normal electromagnets, which dissipate heat and have high power requirements. One such application of powerful electromagnets is in high energy physics where beams of protons and other particles are accelerated to almost light speeds and collided with each other so that more fundamental particles are produced. It is expected that this research will answer fundamental questions such as those about the origin of the mass of particles that make up the Universe.
Levitating trains have been built that use powerful electromagnets made from superconductors. The superconducting electromagnets are mounted on the train. Normal electromagnets, on a guideway beneath the train, repel (or attract) the superconducting electromagnets to levitate the train while pulling it forwards.
A use of large and powerful superconducting electromagnets is in a possible future energy source known as nuclear fusion. When two light nuclei combine to form a heavier nucleus, the process is called nuclear fusion. This results in the release of large amounts of energy without any harmful waste. Two isotopes of hydrogen, deuterium and tritium, will fuse to release energy and helium. Deuterium is available in ordinary water and tritium can be made during the nuclear fusion reactions from another abundantly available element – lithium. For this reason it is called clean nuclear energy. For this reaction to occur, the deuterium and tritium gases must be heated to millions of degrees so that they become fully ionized. As a result, they must be confined in space so that they do not escape while being heated. Powerful and large electromagnets made from superconductors are capable of confining these energetic ions.
An international fusion energy project, known as the International Thermonuclear Experimental Reactor project, located in Saint-Paul-lès-Durance, southern France, aims to demonstrate the feasibility of fusion as a large-scale and carbon-free source of energy that will use large superconducting magnets. However, the project has faced challenges. The previously stated goal was to create the plasma by 2025, but this deadline will have to be postponed. Despite the delays, ITER remains a significant project, and its ultimate goal is to replicate the reactions that power the sun, demonstrating that fusion power can be generated on a commercial scale.
Radiation Shield
A well-known problem to face in the future, long-term, manned missions in deep space is ionizing radiation. Solar particle events (SPE) and Galactic Cosmic Rays (GCR) will threat the health of astronauts exposing them to several kinds of late and acute diseases, even fatal. Several solutions have been proposed to protect crews, based on either energy loss in the interaction with matter is called passive shielding or the deflection of particles by means of magnetic fields is called active shielding. Passive shielding requires thick layers of materials around the spacecraft cabin resulting in large mass increasing. Active shielding is a valid alternative but requires huge superconducting magnets that have to operate in space for years. It would have been unthinkable 55 years ago when the magnetic shielding principle was first proposed, but now, thanks to the progress in magnet technology and to the development of high temperature superconductors as well as of magnesium diboride, active shielding has become a possible option.
The existing literature reports several studies about magnetic shielding of space radiation, however until recent years all of them have based the evaluation of shielding efficiency only on the deflection by means of magnetic field, neglecting the interaction of particle with the materials composing the magnet. Materials act as passive shielding, stopping part of the incoming charged particles, however the interactions also generate secondary particle showers, which give an additional contribution to the astronauts’ radiation dose. A significant part of the secondary particles is neutrons, which cannot be magnetically shielded. Recent studies have shown that the particle-material interactions results in a reduction of the effective shielding power.
Magnetic systems for particle shielding are large superconducting magnets positioned around the spacecraft habitat; the most studied configurations are solenoids and toroids. Solenoids can be arranged in two ways: one large solenoid hosting the cabin within its bore or several solenoids positioned circularly around the spacecraft. In the toroidal configuration, the spacecraft cabin is hosted within the bore of the toroid. While the fringe field is null inside the bore of an ideal toroid, solenoidal configurations require an inner solenoid to cancel the stray field in the habitable module.
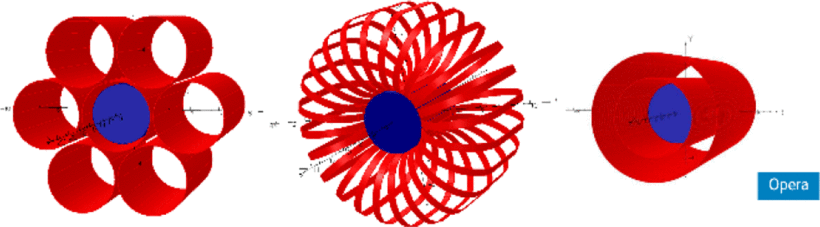
The dimensions of the radiation shield have to be defined on the basis of both the spacecraft characteristics and the launcher size. A possible configuration was evaluated by hypothesizing the use of the Columbus module of the International Space Station as habitable cabin, which is 7 meter long and 4.5 meter in diameter. Due to its very large dimension, the magnetic system is designed to be modular, namely, to be assembled in orbit after having separately launched its parts (magnets and inner support). Consequently, the size of the toroidal magnets was set to fit the fairing of the future heavy launcher SLS Block 1B Cargo
The coils of toroids are subject to inward forces, that is, radially directed to the axis. In the case of a toroid surrounding the spacecraft habitat hosted in its bore, a large mechanical structure is required, strong enough to prevent any risk for the cabin. In the pumpkin configuration, the inner radius of the toroids is small; therefore, the large inward forces experienced by the three coils of each toroid are easily supported by a central bar. Differently, the total radial forces experienced by the toroids, that is, the forces along x and y axes, are relatively weak and directed outward. To support the outward forces, the inner beam of each toroid is connected to a mechanical structure surrounding the cabin. The forces acting on the winding are kept by grids of ropes.
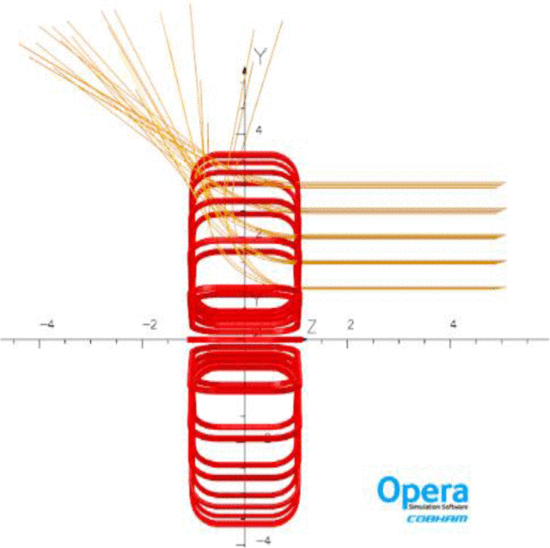
Specific attention must be payed analyzing the azimuthal forces, which result in bending momenta acting on the axis of each toroid. Consequently, a mechanical support is necessary to limit the axis deformation. Such a support is also used to hold forces and torques due to slight construction asymmetries. Each of toroid will be constructed on Earth, the entire structure is designed to be assembled in orbit; therefore, small errors in magnet positioning must be taken into account. Such a radiation shield is able to fully deflect solar particles, protecting astronauts also during intense solar events.